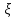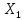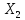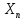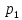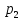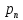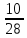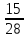- •3. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Свойства вероятности.
- •4.Элементы комбинаторики и схемы выбора.
- •5. Геометрическая вероятность. Свойства вероятности.
- •7. Формула полной вероятности и формула Байеса.
- •8. Схема незовисимых испытаний Бернулли,формула Бернулли.Общая теорема о повторении опытов.
- •9. Общая теорема о повторении опытов. Наиболее вероятное число успехов в схеме Бернулли. Номер первого успешного испытания.
- •10. Предельные теоремы в схеме Бернулли. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
- •11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Закон больших чисел в форме Бернулли.
- •12. Случайные величины и распределения вероятностей. Свойства функции распределения вероятностей.
- •13.Классификация случайных величин. Дискретные распределения (примеры основных распределений)
- •I.Дискретные распределения
- •14. .Классификация случайных величин. Абсолютно непрерывные распределения(примеры основных распределений).
- •I. . Абсолютно непрерывные распределения.
- •15.Нормальное распределение и его свойства.
- •16.Основные распределения случайных величин, применяемые в статистике.
- •17.Мат.Ожидание и его свойства.
- •18.Дисперсия и её свойства
- •20 Числовые характеристики системы двух случайных величин.Ковариация.
- •19.Мода,медиана,моменты,ассиметрия,эксцесс
- •21.Числовые характеристики системы двух случайных величин .Коэффициент корреляции.
- •22.Определение случайной последовательности . Определение сходимости по вероятности .Неравенство Маркова. Неравенство Чебышева.
- •24.Центральная предельная теорема для одинаково распределенных независимых слагаемых. (цпт)
- •25.Определение и описание случайного процесса
- •26.Статистические средние характеристики случайных процессов(сп).
- •27.Стационарные случайные процессы(сп)
- •28.Предмет мат. Статистики
- •29.Средние величины
- •30. Показатели вариации, моменты.
- •31. Статистические оценки параметров распределения. Методы нахождения оценок.
- •32.Метод моментов.
- •34.Интервальные оценки.
12. Случайные величины и распределения вероятностей. Свойства функции распределения вероятностей.
Очень часто результатом опыта является не событие, а величина (число). Повторяя опыты получаем различные значения этой величины. Например время безотказной работы электроприбора предсказать невозможно, это случайная величина.
Определение 1: под случайной величиной (СВ) понимают такую величину, которая в результате опыта принимает неизвестное заранее значение, причем это значение от опыта к опыту меняется.
Определение 2: функция Fξ(x) распределения случайной величины ξ называется функция:
Fξ(x)=P(ξ<x), т.е. Fξ(x) есть вероятность того, что СВ ξ примет значение меньше некоторого x. Случайные величины будем обозначать греческими буквами ξ, η, ζ, тогда x,y,z, ... это значения СВ.
Функция распределения является самой полной характеристикой СВ. Задать СВ значит задать ее функцию распределения, а все это можно сказать о СВ заключено в ее функции распределения.
Свойства функции распределения вероятностей.
Fξ(x) не убывающая функция, т.е. если x₁≤x₂, то Fξ(x₁)≤ Fξ(x₂).
Fξ(x) удовлетворяет следующим соотношениям:
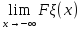 =0,
=0,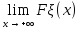 =1
т.е. из определения и свойства следует,
что 0≤Fξ(x)
≤1,
=1
т.е. из определения и свойства следует,
что 0≤Fξ(x)
≤1,
 x.
x.Функция распределения непрерывна слева, т.е.
 =Fξ(x₀),
любая функция удовлетворяющая свойствам
1-3 будет функцией распределения некоторой
СВ.
=Fξ(x₀),
любая функция удовлетворяющая свойствам
1-3 будет функцией распределения некоторой
СВ.P(a≤ξ≤b)= Fξ(a)- Fξ(b).
13.Классификация случайных величин. Дискретные распределения (примеры основных распределений)
Под законом распределения СВ понимают всякую характеристику из которой по определенным правилам можно получить фу-ю распределения СВ.Все распределения можно поделить на три типа:
1.Дискретные
2.Абсалютно непрерывные
3.Синбулярные
I.Дискретные распределения
Определения:СВ
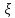 имеет
дискретное распределение (является
дискретной) если она принимае конечное
или счетное множество значений с
определенными вероятностями ,т.е.
существует конечный или счётный набор
значений СВ
имеет
дискретное распределение (является
дискретной) если она принимае конечное
или счетное множество значений с
определенными вероятностями ,т.е.
существует конечный или счётный набор
значений СВ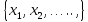
 :
:
1.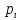 =Р(
=Р(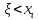 )
)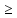 0
0
2.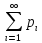 =1(с-во
нармировки ДСВ).ДСВ-дискретная случайная
величина. Если число значений СВ
конечно,т.е.
=1(с-во
нармировки ДСВ).ДСВ-дискретная случайная
величина. Если число значений СВ
конечно,т.е.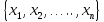 ,то
второе свойство выглядит так:
,то
второе свойство выглядит так: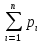
Определения:
Таблицей распределения ДСВ
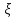 называют таблицу вида:
называют таблицу вида:
|
|
|
|
……. |
|
|
Р |
|
|
…….. |
|
В верхней строке, которой по возрастанию перечислены значения СВ ,а в нижней вероятности этих значений.
Определения:
функция распределения Д СВ определяется
по ф-ле: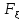 =
P(
=
P(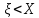 )=
)= при
при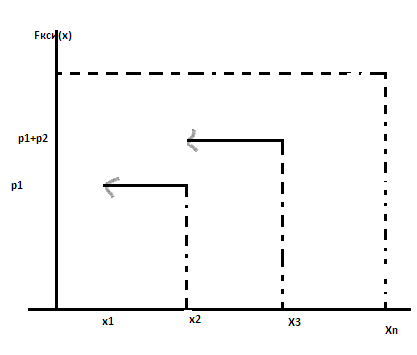
при
х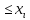 ,
,
при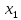
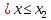 .
.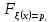
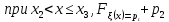

При
х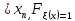
Примеры основных дискретных распределений.
1.Выражденное
распределение в т.а имеет СВ
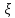 со следующей таблицей распределения:
со следующей таблицей распределения:
|
|
а |
|
р |
1 |
Т.е.
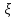 =а=const
=а=const
2.Распределение
Бернулли с параметром р
имеет
СВ
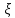 принимающее значение
принимающее значение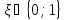 с вероятностями:
с вероятностями:
Р(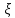 =0)=1-р
=0)=1-р
Р(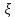 =1)=р,тогда
таблица распределения имеет вид.
=1)=р,тогда
таблица распределения имеет вид.
|
|
0 |
1 |
|
р |
1-р |
р |
3.Биноминальное
распределение с параметрами n,p,0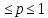 имеет СВ
имеет СВ
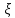 принимающее значение
принимающее значение
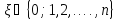 c
вероятностями :
c
вероятностями :
Р
(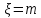 )=
)=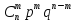 ,это
распределение называется биноминальным,т.
К. вероятности этого распределения
могут быть получены при разложении
,это
распределение называется биноминальным,т.
К. вероятности этого распределения
могут быть получены при разложении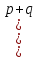 по формулам бинома Ньютона.
по формулам бинома Ньютона.
4.Геометрическое
распределение с параметром р
имеет СВ
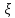 принимающее значение
принимающее значение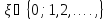 с вероятностями Р (
с вероятностями Р (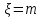 )=р
)=р
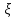 имеет смысл номера первого успешного
испытания в схеме Бернулли с вероятностью
успеха р.
имеет смысл номера первого успешного
испытания в схеме Бернулли с вероятностью
успеха р.
5.Распределение
Пуассона с параметром
 ,
,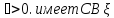 принимающее
значение
принимающее
значение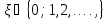 с вероятностями Р (
с вероятностями Р (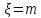 )=
)=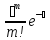
6.Гипергеометрическое распределение.
Пусть
имеется
N
шаров среди которых M1-бЕлых
и М2-черных,тогда М1+М2=
N,наудачу
извлекают n
шаров,тогда
СВ
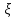 имеет смысл число белых шаров среди
извлекающих,т.о.
имеет смысл число белых шаров среди
извлекающих,т.о.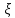 принимает значение
принимает значение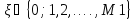 ,с вероятностями Р (
,с вероятностями Р (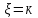 )=
)=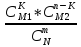
Пример: среди 8 часов поступивших в ремонт 2-е с поломкой оси. НА удачу взято 3-е часов. Составить з-н распределения числа часов с поломанной осью среди взятых трёх.
|
|
0 |
1 |
2 |
|
р |
|
|
|
Т.к. 2-е только с поломкой оси.
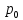 =Р(
=Р(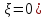 =
=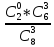 =
=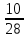 ,
,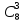 -все
возможные исходы,
-все
возможные исходы,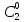 -т.к.
-т.к.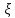 должно равняться 0,то мы 0 часов из
должно равняться 0,то мы 0 часов из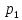 =Р(
=Р( =
= =
=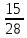 2 с поломанными осями и останется3-ое
из оставшихся
2 с поломанными осями и останется3-ое
из оставшихся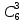
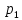 =Р(
=Р(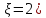 =
= =
=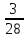 Контроль:
Контроль: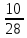 +
+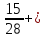
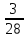 =1
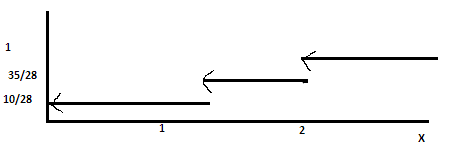
Построить
ф-ю распределения СВ
=1
Построить
ф-ю распределения СВ
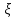 :
:
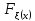 =
P(
=
P(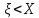 )=
)=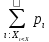 -функция распределения
-функция распределения
При х
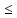 0,
0,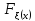 =0-всегда
на первом интервале
=0-всегда
на первом интервале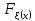 =0
=0При 0
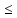 х
х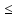 1
,
1
,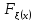 =
=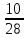
При 1
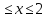
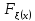 =
=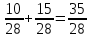
При х
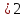 ,
,
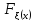 =
=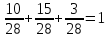 всегда на последнем интервалеF(X)=1
всегда на последнем интервалеF(X)=1