
- •3. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Свойства вероятности.
- •4.Элементы комбинаторики и схемы выбора.
- •5. Геометрическая вероятность. Свойства вероятности.
- •7. Формула полной вероятности и формула Байеса.
- •8. Схема незовисимых испытаний Бернулли,формула Бернулли.Общая теорема о повторении опытов.
- •9. Общая теорема о повторении опытов. Наиболее вероятное число успехов в схеме Бернулли. Номер первого успешного испытания.
- •10. Предельные теоремы в схеме Бернулли. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
- •11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Закон больших чисел в форме Бернулли.
- •12. Случайные величины и распределения вероятностей. Свойства функции распределения вероятностей.
- •13.Классификация случайных величин. Дискретные распределения (примеры основных распределений)
- •I.Дискретные распределения
- •14. .Классификация случайных величин. Абсолютно непрерывные распределения(примеры основных распределений).
- •I. . Абсолютно непрерывные распределения.
- •15.Нормальное распределение и его свойства.
- •16.Основные распределения случайных величин, применяемые в статистике.
- •17.Мат.Ожидание и его свойства.
- •18.Дисперсия и её свойства
- •20 Числовые характеристики системы двух случайных величин.Ковариация.
- •19.Мода,медиана,моменты,ассиметрия,эксцесс
- •21.Числовые характеристики системы двух случайных величин .Коэффициент корреляции.
- •22.Определение случайной последовательности . Определение сходимости по вероятности .Неравенство Маркова. Неравенство Чебышева.
- •24.Центральная предельная теорема для одинаково распределенных независимых слагаемых. (цпт)
- •25.Определение и описание случайного процесса
- •26.Статистические средние характеристики случайных процессов(сп).
- •27.Стационарные случайные процессы(сп)
- •28.Предмет мат. Статистики
- •29.Средние величины
- •30. Показатели вариации, моменты.
- •31. Статистические оценки параметров распределения. Методы нахождения оценок.
- •32.Метод моментов.
- •34.Интервальные оценки.
14. .Классификация случайных величин. Абсолютно непрерывные распределения(примеры основных распределений).
Под законом распределения СВ понимают всякую характеристику из которой по определенным правилам можно получить фу-ю распределения СВ.Все распределения можно поделить на три типа:
1.Дискретные
2.Абсалютно непрерывные
3.Синбулярные
I. . Абсолютно непрерывные распределения.
Определение1:
СВ
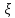 имеет
абсолютно непрерывное распределение,
если существует неотрицательная функция
имеет
абсолютно непрерывное распределение,
если существует неотрицательная функция
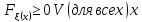 ,такая
чтобы функция распределения была
представлена в виде:
,такая
чтобы функция распределения была
представлена в виде:
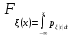 ,
,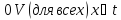
Определение2:
ф-я
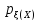 называется плотностью распределения
вероятностей СВ
называется плотностью распределения
вероятностей СВ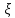 .СВ
.СВ имеющий абсолютно непрерывное
распределение называется непрерывной.
имеющий абсолютно непрерывное
распределение называется непрерывной.
Свойства плотности распределения вероятности:
1.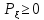 ,
,
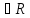
2.
С-во нормировки
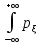 dt=1
dt=1
Определение3:график
ф-и
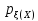 называют кривой распределения по
свойству нормировки,площадь под
распределения =1.Если некоторая фу-я
р(х) обладает свойствами 1,2 ,то существует
СВ
называют кривой распределения по
свойству нормировки,площадь под
распределения =1.Если некоторая фу-я
р(х) обладает свойствами 1,2 ,то существует
СВ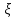 для которой она будет плотностью
распределения вероятности.
для которой она будет плотностью
распределения вероятности.
3.Если
,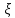 -непрерывная
СВ ,то Р(
-непрерывная
СВ ,то Р(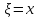 )=0,
)=0,
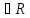
4.Р(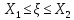 )=
Р(
)=
Р( )=
Р(
)=
Р(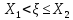 )=
Р(
)=
Р(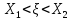 )=
)=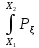 (х)dx
(х)dx
5.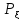 (х)=
(х)=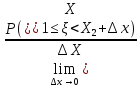
6. (х)=
(х)=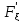 (x)=P=1
(x)=P=1
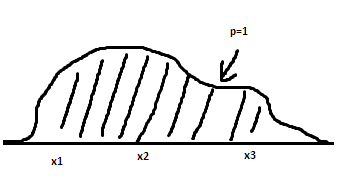 абсолютно
непрерывное распределение.
абсолютно
непрерывное распределение.
Примеры основных непрерывных распределений
I.Равномерное
распределение на отрезке
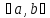 имеет СВ
имеет СВ
 с плотностью вероятности .
с плотностью вероятности .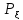 (х)=
(х)=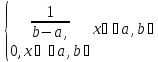 =(расстояние с постоянной плотностью)
=(расстояние с постоянной плотностью)
=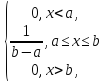 ,
,
Построим ф-ю распределения вероятности:
1)При
х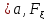 (X)=
(X)=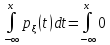 dt=0(всегда
на первом интервале =0)
dt=0(всегда
на первом интервале =0)
2)при (X)=
(X)=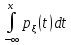 =
=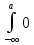 dt+
dt+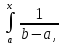 dt=
dt=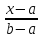
3)при
 (X)=
(X)=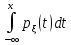 =
=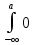 dt+
dt+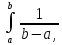 dt+
dt+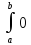 dt=1(всегда
на последнем равно 1)
dt=1(всегда
на последнем равно 1)
Функция распределения:
.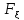 (х)
=
(х)
=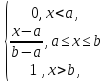 ,
,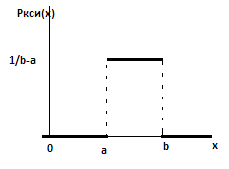
Значение от а до b равновероятны,а значения меньше a и больше b невозможны.
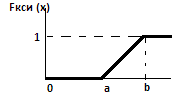
II.Показательное(экспоненциальное)
распределение имеет
СВ
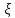 с плотностью распределения вероятности
:
с плотностью распределения вероятности
:
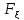 (х)=
(х)=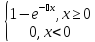
Графики:
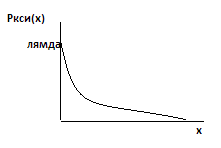
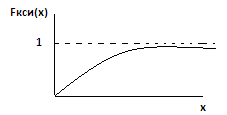
Данное распределение обладает свойством несторения,которая заключается в следующем:
Р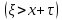 =
Р
=
Р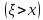
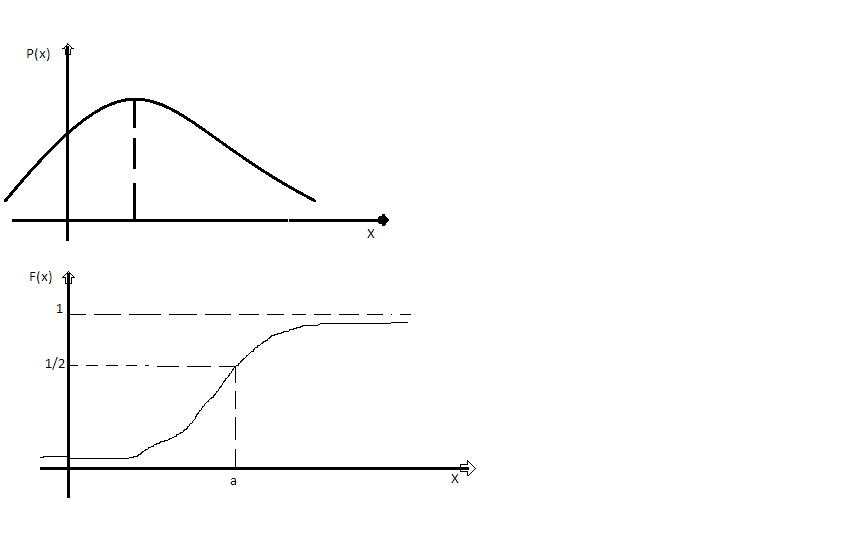
15.Нормальное распределение и его свойства.
СВ
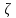 имеет нормальное распределение, если
её плотность распределения вероятностей
имеет вид:
имеет нормальное распределение, если
её плотность распределения вероятностей
имеет вид: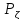 (X)=
(X)=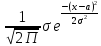 ,а
функция распределения след-я:
,а
функция распределения след-я: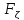 (x)=
(x)=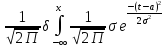 dt
dt
СВ
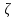 имеет
стандартное нормальное распределение
,если
имеет
стандартное нормальное распределение
,если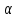 =0,а
=0,а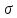 =1:
=1: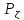 (X)=
(X)=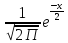 Функция
распределения стандартного нормального
з-на имеет вид:
Функция
распределения стандартного нормального
з-на имеет вид: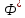 (х)=
(х)=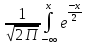 dt
dt
Свойства
нормальной случайной величины с
параметром а,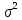 :
:
 .Функция
распределения СВ
.Функция
распределения СВ
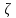 выражается через функцию Ф(Х) следующим
образом:
выражается через функцию Ф(Х) следующим
образом: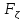 (x)=
(x)=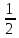 +Ф(
+Ф(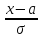 )
)
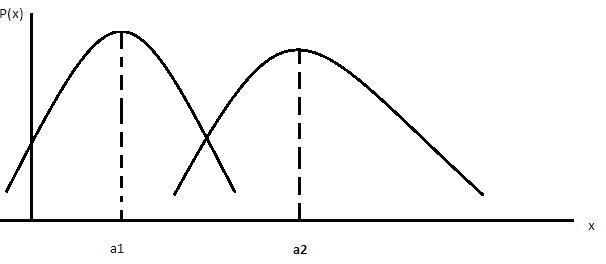
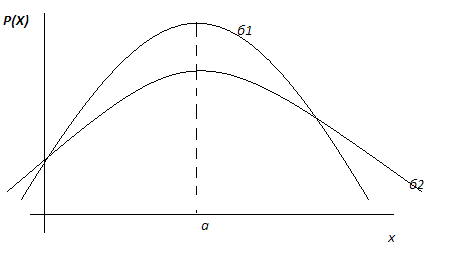
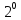 .График
плотности распределения при изменении
а и
.График
плотности распределения при изменении
а и
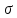 ведет себя следующим образом:
ведет себя следующим образом:
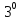 .Вероятность
попадания нормальной СВ в интервал
может быть рассчитано :
.Вероятность
попадания нормальной СВ в интервал
может быть рассчитано :
P(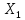 <
<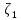 <
< )=
)=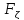 (
(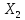 )-
)-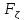 (
( )
)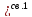 Ф(
Ф(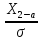 )-
Ф(
)-
Ф(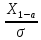 )
)
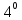 .P(
.P(
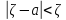 )=
2Ф (
)=
2Ф (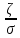 )-вероятность
отклонения от велечины
)-вероятность
отклонения от велечины
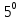 .”Правило
трёх
.”Правило
трёх
 “:если
“:если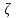 имеется нормальное с параметрами а,
имеется нормальное с параметрами а,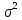 ,то
практически достоверно ,что её значение
заключены в интервале (а-3
,то
практически достоверно ,что её значение
заключены в интервале (а-3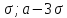 ).
).
P(
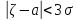 )=
2Ф (
)=
2Ф (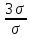 )=2Ф(3)=0,997(св.4)
)=2Ф(3)=0,997(св.4)
16.Основные распределения случайных величин, применяемые в статистике.
Рассмотрим три основных з-на распределения, составляющих необходимый аппарат для построения в дальнейшем статистических критериев.
I.Пусть
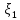 ,
,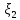 ,
,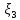 …..
, ,
…..
, ,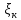 -независимые
СВ, распределённые по стандартному
нормальному з-ну:
-независимые
СВ, распределённые по стандартному
нормальному з-ну:
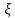
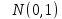 .
.
Говорят,что
сумма квадратов этих СВ распределена
по з-ну
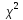 (
(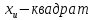 )
с кстепенями
свободы.Эту
СВ обозначают
)
с кстепенями
свободы.Эту
СВ обозначают
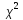 (к):
(к):
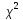 (к)=
(к)= .
.
Графики
плотности распределения
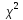 (к)
при различных к изображены на рис.:
(к)
при различных к изображены на рис.:
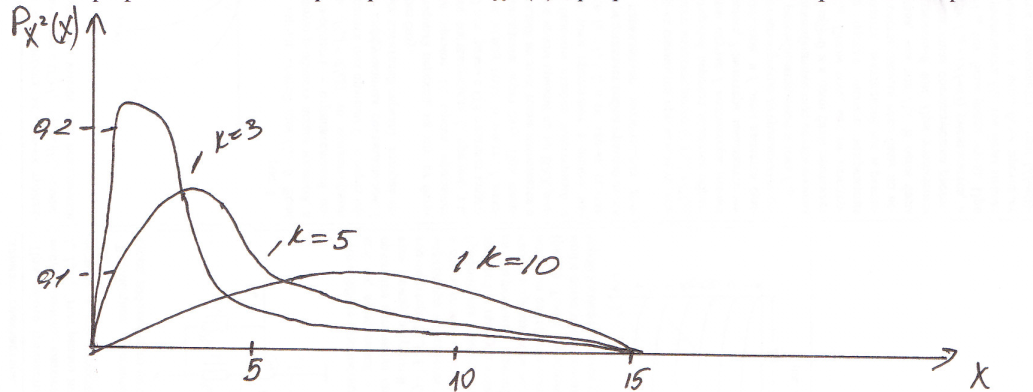
1.Случайная
величина
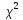 (к)
принимает неотрицательные значения,
то есть имеет нулевую плотность
распределения при х
(к)
принимает неотрицательные значения,
то есть имеет нулевую плотность
распределения при х 0.Это следует из определения.
0.Это следует из определения.
2.При
большом числе степеней свободы k
распределение
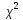 (к)
близко к нормальному.Этот факт
иллюстрируется графиком на рис.
(к)
близко к нормальному.Этот факт
иллюстрируется графиком на рис.
3.Мат.ожидание
СВ,распределенной по з-ну
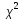 (к),равноk..
(к),равноk..
II.Пусть
СВ
 з-ну распределённые по стандартному
нормальному з-ну:
з-ну распределённые по стандартному
нормальному з-ну: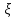
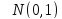 .Распределение
Стьюдента (или t-распределение)
с k
степенями свободы называется распределение
случайной величины
.Распределение
Стьюдента (или t-распределение)
с k
степенями свободы называется распределение
случайной величины
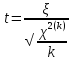 ,где
,где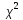 (к)-независимая
от
(к)-независимая
от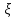 СВ,имеющая
распределение
СВ,имеющая
распределение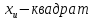 с k степенями свободы.
Графики плотности распределения
Стьюдента при различном числе степени
свободы приведены на рис.Из вида графиков
и определения можно сделать некоторые
наблюдения о свойствах распределения
Сьюдента.
с k степенями свободы.
Графики плотности распределения
Стьюдента при различном числе степени
свободы приведены на рис.Из вида графиков
и определения можно сделать некоторые
наблюдения о свойствах распределения
Сьюдента.
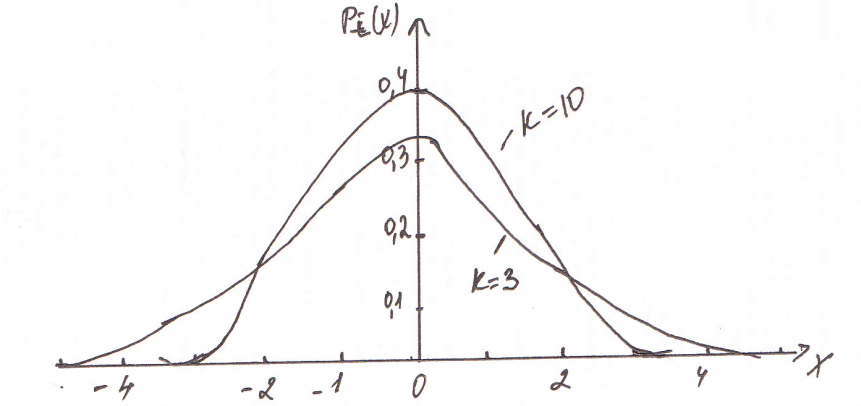
1.
Распределения Сьюдента симметрично,
причем М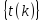 =0
=0
2.При
больших k распределения Сьюдента близко
к нормальному распределению
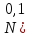 ).
).
III.
На основе распределения
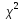 вводится еще одна СВ.Распределение
Фишера(Фишера-Снедекора или F-распределением)
с
вводится еще одна СВ.Распределение
Фишера(Фишера-Снедекора или F-распределением)
с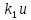
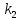 степенями свободы называется распределение
СВ:
степенями свободы называется распределение
СВ:
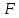 (
(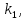
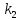 )=
)=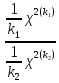 где
где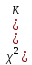 )
и
)
и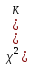 )-
независимыеСВ,имеющие
)-
независимыеСВ,имеющие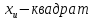 распределение соответственно с
распределение соответственно с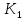 и
и степенями свобод.
степенями свобод.
1.из
определения видно, что данная СВ не
может принимать отрицательные значения,то
есть имеет нулевую плотность распределения
вероятностей при
х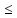 0.
0.
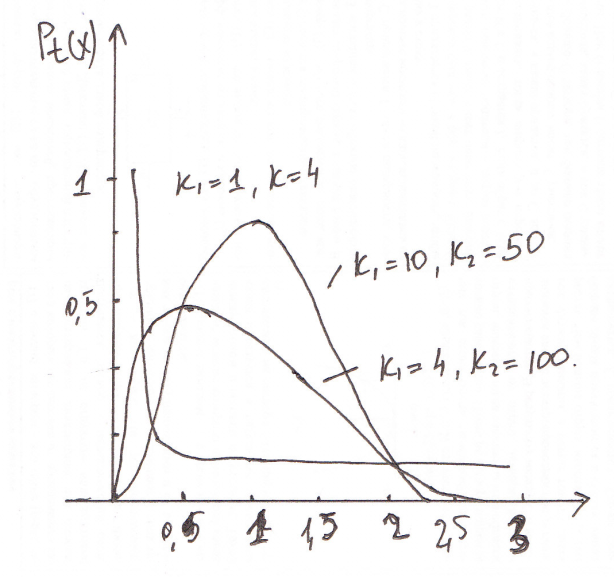
2.Графики
плотности распределения при различном
числе степеней свободы изображены на
рис.При некоторых значениях числа
степеней свободы
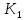 и
и F-распределение
прибли жается к нормальному.
F-распределение
прибли жается к нормальному.
 .
.
