- •3. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Свойства вероятности.
- •4.Элементы комбинаторики и схемы выбора.
- •5. Геометрическая вероятность. Свойства вероятности.
- •7. Формула полной вероятности и формула Байеса.
- •8. Схема незовисимых испытаний Бернулли,формула Бернулли.Общая теорема о повторении опытов.
- •9. Общая теорема о повторении опытов. Наиболее вероятное число успехов в схеме Бернулли. Номер первого успешного испытания.
- •10. Предельные теоремы в схеме Бернулли. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
- •11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Закон больших чисел в форме Бернулли.
- •12. Случайные величины и распределения вероятностей. Свойства функции распределения вероятностей.
- •13.Классификация случайных величин. Дискретные распределения (примеры основных распределений)
- •I.Дискретные распределения
- •14. .Классификация случайных величин. Абсолютно непрерывные распределения(примеры основных распределений).
- •I. . Абсолютно непрерывные распределения.
- •15.Нормальное распределение и его свойства.
- •16.Основные распределения случайных величин, применяемые в статистике.
- •17.Мат.Ожидание и его свойства.
- •18.Дисперсия и её свойства
- •20 Числовые характеристики системы двух случайных величин.Ковариация.
- •19.Мода,медиана,моменты,ассиметрия,эксцесс
- •21.Числовые характеристики системы двух случайных величин .Коэффициент корреляции.
- •22.Определение случайной последовательности . Определение сходимости по вероятности .Неравенство Маркова. Неравенство Чебышева.
- •24.Центральная предельная теорема для одинаково распределенных независимых слагаемых. (цпт)
- •25.Определение и описание случайного процесса
- •26.Статистические средние характеристики случайных процессов(сп).
- •27.Стационарные случайные процессы(сп)
- •28.Предмет мат. Статистики
- •29.Средние величины
- •30. Показатели вариации, моменты.
- •31. Статистические оценки параметров распределения. Методы нахождения оценок.
- •32.Метод моментов.
- •34.Интервальные оценки.
31. Статистические оценки параметров распределения. Методы нахождения оценок.
Основная задача теории оценок выглядит следующим образом. Имеется случайная величина ξ, для которой известен вид ее плотности распределения вероятностей с точностью до неизвестных параметров. Например, известно, что величина ξ нормальная, то есть ее плотность вероятностей имеет вид
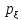 (x)
=
(x)
=
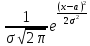 ,
,
по параметры а и σ, характеризующие эту плотность вероятностей, нам неизвестны. Нашей задачей является оценка этих неизвестных параметров. Будем пока считать, для простоты, что у нас имеется всего лишь один неизвестный параметр θ, подлежащий оценке.
Разумеется, оценить неизвестный параметр можно только на
основе
опытных данных X=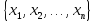 .
Имея выборкуX, мы
.
Имея выборкуX, мы
должны
указать число
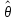 ,
которое близко к истинному значению
неизвестного параметра θ, то есть мы
должны указатьоценку
,
которое близко к истинному значению
неизвестного параметра θ, то есть мы
должны указатьоценку 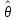 неизвестного параметра θ. Значит, мы
должны каждой выборкеX поставить
в соответствии некоторое число
неизвестного параметра θ. Значит, мы
должны каждой выборкеX поставить
в соответствии некоторое число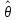 ,
которое будет называться оценкой
неизвестного параметра θ. Другими
словами, оценка
,
которое будет называться оценкой
неизвестного параметра θ. Другими
словами, оценка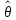 есть функция от опытных данных:
есть функция от опытных данных:
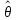 =T(x1,x2,…,xn)
=T(X).
=T(x1,x2,…,xn)
=T(X).
Задачей теории оценки как раз и является указание вида функции T(X).
Ясно, что функцию Т(Х) следует выбирать таким образом, чтобы ее значения как можно точнее оценивали значения неизвестного параметра θ. К оценкам предъявляются требования, ограничивающие выбор функции Т(Х). Рассмотрим эти требования.
1. Несмещенность - требование отсутствия систематических ошибок, или требование того, чтобы оценка в среднем совпадала с истинным значением неизвестного параметра:
М(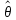 )
= θ .
)
= θ .
2. Эффективность. Оценкой качества оценка является еевариация:
V(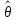 )
= М(
)
= М(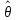 -θ)2.
-θ)2.
Для несмещенной оценки она совпадает, очевидно, с дисперсией. Оценка называется эффективной, если ее вариация является минимальной среди вариаций всех возможных оценок параметра θ, вычисленных по одному и тому же объему выборки п.
3. Состоятельность. Данное требование состоит в том, чтобы
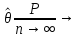 θ.
θ.
Желательно использовать оценки, удовлетворяющие одновременно трем перечисленным требованиям.
Несмещенной
оценкой математического ожидания
случайной величины ξ служит выборочная
средняя
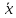 .
Смещенной оценкой дисперсии
случайной величины ξ, служит выборочная
дисперсия
.
Смещенной оценкой дисперсии
случайной величины ξ, служит выборочная
дисперсия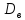 .
Несмещенной оценкой дисперсии
случайной величины ξ служит «исправленная»
выборочная дисперсия
.
Несмещенной оценкой дисперсии
случайной величины ξ служит «исправленная»
выборочная дисперсия
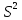 =
=
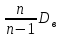 =
=
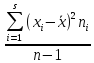 .
.
Точечной называют оценку, которая определяется одним числом.
32.Метод моментов.
Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов (начальных или центральных) соответствующим эмпирическим моментам того же порядка.
Напомним, что теоретические моменты для дискретной величины определяются по формулам:
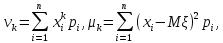
для непрерывных:
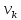 =
=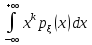 ,
,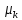 =
=
Если распределение определяется одним параметром, то для его отыскания достаточно одного уравнения, чаще всего используют уравнение
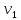 =
=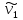 ,то естьМξ =
,то естьМξ =
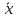 .
.
Если распределение определяется двумя параметрами, то чаще всего используют систему:
 ,
то есть
,
то есть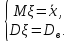
Разумеется, что для вычисления выборочных характеристик надо располагать выборкой.
Пример 14.1. Найти оценку параметраX распределения Пуассона с помощью метода моментов.
Решение. Распределение Пуассона задается вероятностями
рк
=
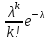 ,
к= 0,1,2,... . В данном случае для нахождения
единственного параметра достаточно
приравнять
,
к= 0,1,2,... . В данном случае для нахождения
единственного параметра достаточно
приравнять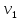 =
=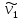 илиМξ =
илиМξ =
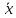 .
Математическое ожидание распределения
Пуассона равноλ. Следовательно,
оценка параметра λ закона Пуассона
есть выборочная средняя
.
Математическое ожидание распределения
Пуассона равноλ. Следовательно,
оценка параметра λ закона Пуассона
есть выборочная средняя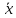 :
:
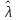 =
=
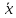 .
.
Пример 14.2. Случайная величина ξ, - время безотказной рабо-ты прибора, имеет показательное распределение:
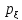 (x)
= λ
(x)
= λ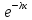 ,
x ≥ 0
,
x ≥ 0
Ниже приведено эмпирическое распределение среднего времени работы п = 200 элементов:
|
|
2,5 |
7,5 |
12,5 |
17,5 |
22,5 |
27,5 |
|
|
133 |
45 |
15 |
4 |
2 |
1 |
Найти методом моментов точечную оценку неизвестного параметра показательного распределения.
Решение.
Будем использовать уравнение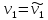 ,
то есть
,
то есть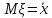 .
.
Математическое ожидание показательного распределения равно
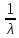 .
.
Значит
 =
=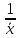 .
.
Определим выборочную среднюю:
 =
=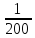 (2,5∙133
+ 7,5 ∙45 + 12,5∙15 +17,5∙4 + 22,5∙2 + 27,5∙1) = 5.
(2,5∙133
+ 7,5 ∙45 + 12,5∙15 +17,5∙4 + 22,5∙2 + 27,5∙1) = 5.
Тогда получим оценку параметра λ:
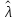 =
=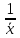 =
=
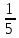 = 0,2
= 0,2
Оценки метода моментов состоятельны, однако по эффективности они не являются наилучшими. Тем не менее метод моментов часто используется на практике, так как приводит к сравнительно простым вычислениям.
33.Метод максимального правдоподобия.
Основным методом получения оценок параметров генеральной совокупности по данным выборки является метод максимального правдоподобия, предложенный Р.Фишером,
Основу
метода составляет функция правдоподобия,
выражающая плотность вероятности
(вероятность) совместного появления
результатов выборки ,
,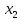 ,…,
,…,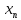 :
:
L(х1,х2,…,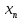 ;θ)
=L(X;θ) =p(х1,
θ)p(х2, θ)…p(хn,
θ), гдев случае непрерывного
распределенияp(x,θ)
- плотность распределения вероятностей
исследуемой случайной величины,в
случаедискретного распределенияp(x,θ)
- вероятность того, что в результате
испытания случайная величина примет
значениех.
;θ)
=L(X;θ) =p(х1,
θ)p(х2, θ)…p(хn,
θ), гдев случае непрерывного
распределенияp(x,θ)
- плотность распределения вероятностей
исследуемой случайной величины,в
случаедискретного распределенияp(x,θ)
- вероятность того, что в результате
испытания случайная величина примет
значениех.
Согласно
методу максимального правдоподобия в
качестве оценки неизвестного параметра
θ принимается
такое значение
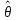 ,
которое максимизирует функцию L.
То есть оценка
,
которое максимизирует функцию L.
То есть оценка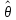 является точкой максимума функции
правдоподобия.
является точкой максимума функции
правдоподобия.
Нахождение
оценки
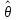 упрощается, если максимизировать
не саму функциюL, aInL,поскольку
максимум обеих функций достигается
при одном и том же значенииθ.
ФункцияInL, называетсялогарифмической функцией правдоподобия.
упрощается, если максимизировать
не саму функциюL, aInL,поскольку
максимум обеих функций достигается
при одном и том же значенииθ.
ФункцияInL, называетсялогарифмической функцией правдоподобия.
Точку максимума функции InLпо аргументуθ можно искать, например, так:
1.
Найти производную
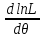 .
.
2.
Найти критическую точку θ*
из уравнения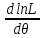 = 0.
= 0.
3.
Найти вторую производную
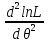 ,
если вторая прозводная
,
если вторая прозводная
при θ = θ* отрицательна, то θ* - точка максимума.
Найденную
точку максимума θ* принимают в качестве
оценки максимального правдоподобия
параметра θ,
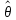 = θ*.
= θ*.
В
случае, когда надо оценить не один
параметр θ, а несколько (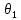 ,
, ,…,
,…,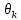 ),
оценки максимального правдоподобия
для этих параметров находят из системы
уравнений:
),
оценки максимального правдоподобия
для этих параметров находят из системы
уравнений:
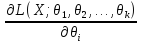 = 0, i =
= 0, i =
 .
.
Пример 14.3. Для случайной величины распределенной по закону Пуассона, по результатам выборких1,х2,...,х„ оценить неизвестный параметрλ.
Решение. Для распределения Пуассона
p(xi;λ)
= P(ξ = xi)
=
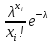 ,
i =
,
i =
 .
.
Построим функцию правдоподобия:
L
=
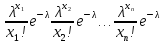 =
=
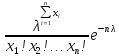 .
.
Перейдем к логарифмической функции правдоподобия:
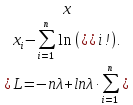
Дифференцируя это равенство, имеем
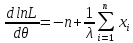
Приравнивая нулю, имеем
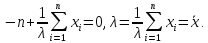
Находя вторую производную, получим
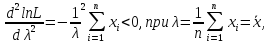
для распределения Пуассона xi ≥ 0.
Следовательно
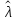 =
= .
.
Пример
14.4. Пусть
случайная величина ξ имеет показательное
распределение с плотностью вероятностей
р(х,λ) =
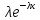 ,
x
≥ 0. Требуется по результатам выборки
х1,
х2,…,xп
найти оценку
неизвестного параметра λ.
,
x
≥ 0. Требуется по результатам выборки
х1,
х2,…,xп
найти оценку
неизвестного параметра λ.
Решение. Для показательного распределения функция правдоподобия имеет вид:
L(X,λ)
= λ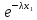 λ
λ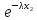 …
…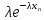 =
=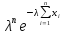 .
.
Логарифмируя эту функцию, получим:
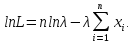
Тогда
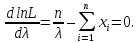
Отсюда
λ
=
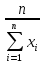 =
=
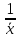 .
.
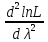 = -
= -
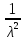 < 0
< 0
Значит,
оценка неизвестного параметра имеет
вид
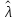 =
=
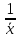 .
.
Пример 14.5. Для нормально распределенной случайной величины ξ по результатам выборки х1, х2,…,xп найти оценку неизвестных параметров а и σ.
Решение. Плотность распределения вероятностей нормального
закона имеет вид:
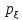 = (x;а,σ)
=
= (x;а,σ)
=
 .
.
В этом случае функция правдоподобия имеет вид:
Прологарифмировав L, получим:

Дифференцируя по а и σ, будем иметь:
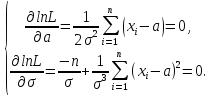
Отсюда находим оценки неизвестных параметров а и σ.
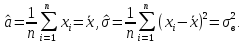
Важность метода максимального правдоподобия связана с оптимальными свойствами его оценок. Основной недостаток метода максимального правдоподобия - трудность вычисления оценок, связанных с решением уравнений правдоподобия, чаще всего нелинейных. Существенно и то, что для построения оценок максимального правдоподобия и обеспечения их «хороших» свойств необходимо знание чипа анализируемого закона распределения р(х,θ), что во многих случаях оказывается практически нереальным.
Широкое распространение в практике статистических исследований получил метод наименьших квадратов, так как он, во-первых, не требует знания закона распределения выборочных данных, во-вторых, достаточно хорошо разработан в плане вычислительной реализации. Суть егозаключается в том, чтооценка определяется из условия минимизации суммы квадратов отклонений выборочных данных от определяемой оценки.
Применение метода наименьших квадратов будет рассмотрено при решении задач корреляционного и регрессионного анализа.