
- •3. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Свойства вероятности.
- •4.Элементы комбинаторики и схемы выбора.
- •5. Геометрическая вероятность. Свойства вероятности.
- •7. Формула полной вероятности и формула Байеса.
- •8. Схема незовисимых испытаний Бернулли,формула Бернулли.Общая теорема о повторении опытов.
- •9. Общая теорема о повторении опытов. Наиболее вероятное число успехов в схеме Бернулли. Номер первого успешного испытания.
- •10. Предельные теоремы в схеме Бернулли. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
- •11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Закон больших чисел в форме Бернулли.
- •12. Случайные величины и распределения вероятностей. Свойства функции распределения вероятностей.
- •13.Классификация случайных величин. Дискретные распределения (примеры основных распределений)
- •I.Дискретные распределения
- •14. .Классификация случайных величин. Абсолютно непрерывные распределения(примеры основных распределений).
- •I. . Абсолютно непрерывные распределения.
- •15.Нормальное распределение и его свойства.
- •16.Основные распределения случайных величин, применяемые в статистике.
- •17.Мат.Ожидание и его свойства.
- •18.Дисперсия и её свойства
- •20 Числовые характеристики системы двух случайных величин.Ковариация.
- •19.Мода,медиана,моменты,ассиметрия,эксцесс
- •21.Числовые характеристики системы двух случайных величин .Коэффициент корреляции.
- •22.Определение случайной последовательности . Определение сходимости по вероятности .Неравенство Маркова. Неравенство Чебышева.
- •24.Центральная предельная теорема для одинаково распределенных независимых слагаемых. (цпт)
- •25.Определение и описание случайного процесса
- •26.Статистические средние характеристики случайных процессов(сп).
- •27.Стационарные случайные процессы(сп)
- •28.Предмет мат. Статистики
- •29.Средние величины
- •30. Показатели вариации, моменты.
- •31. Статистические оценки параметров распределения. Методы нахождения оценок.
- •32.Метод моментов.
- •34.Интервальные оценки.
30. Показатели вариации, моменты.
Средние величины не отражают изменчивости (вариации) значений признака.
Простейшим показателем вариации является вариационный
размах R =хтах - xmin .
Наибольший интерес представляет мера рассеяния наблюдений вокруг средней арифметической — дисперсия.
Дисперсией (выборочной дисперсией) вариационного ряда называется величина
При
расчете дисперсии и других числовых
характеристик интервальных рядов в
качестве
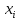 ,
также используют середины интервалов.
Часто для вычисления дисперсии используют
упрощенную формулу:
,
также используют середины интервалов.
Часто для вычисления дисперсии используют
упрощенную формулу:
Dв=
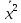 -
-
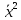
где
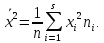
Если признак ξ измеряется в метрах, то, очевидно, его дисперсия - в метрах квадратных. Желательно в качестве меры вариации иметь характеристику, выраженную в тех же единицах, что и значения признака. Такой характеристикой является среднее квадратическое отклонение:
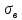 =
=
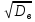
Отношение среднего квадратического отклонения к средней величине признака, выраженное в процентах, называют коэффициентом вариации:
ν =
 ∙100%
∙100%
Если коэффициент вариации признака, принимающего только положительные значения, высок (например, более 100 %), то, как правило, это свидетельствует о неоднородности значений признака.
Выборочная
дисперсия обладает свойствами,
аналогичными свойствам дисперсии
случайной величины. Отмстим следующие:
1.
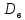 (C) = 0, C
= const;
(C) = 0, C
= const;
2.
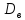 (Cx) = C2
(Cx) = C2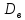 (x),
C = const;
(x),
C = const;
3.
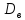 (C+x) =
(C+x) =
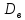 (x),C
= const;
(x),C
= const;
4.
Если выборкиX
иY независимы,
то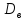 (х
+ у) =
(х
+ у) =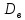 (х)
+
(х)
+
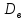 (y).
(y).
Пример 13.1. Вычислить дисперсию, среднее квадратическое отклонение и коэффициент вариации напряжения тока в электросети для примера 11.1.
Решение.
Вычислим
дисперсию по упрощенной формуле
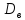 =
=
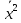 -
-
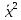 .
.
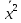 =
=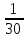 (1062+ 1072∙3 + 1082∙4+I092∙6
+ 1102∙8 +1112∙5
+ 1122∙2 + + 1132)=11992,9.
(1062+ 1072∙3 + 1082∙4+I092∙6
+ 1102∙8 +1112∙5
+ 1122∙2 + + 1132)=11992,9.
D= 11992,9 - 109,52= 2,65.
Среднее
квадратичеcкое отклонение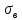 =
=
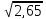 =1,63. Вариация
=1,63. Вариация
v
=
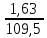 ∙ 100 % = 1,49 %.
∙ 100 % = 1,49 %.
Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия - выборочных (эмпирических) моментов.
Начальный
момент
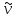 k
k-го порядка
вариационного ряда определяется по
формуле:
k
k-го порядка
вариационного ряда определяется по
формуле:

Центральный
момент
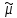 k
k-го порядка
вариационного ряда определяется по
формуле:
k
k-го порядка
вариационного ряда определяется по
формуле:
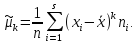
Очевидно,
что
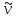 1=
1=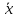 ,
,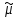 1
= 0,
1
= 0,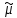 2
=
2
=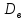
Коэффициентом асимметрии вариационного ряда называется число
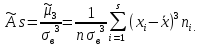
Если
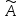 s= 0 , то распределение имеет симметричную
форму, то сеть варианты, равноудаленные
от
s= 0 , то распределение имеет симметричную
форму, то сеть варианты, равноудаленные
от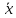 ,
имеют одинаковую частоту. При
,
имеют одинаковую частоту. При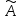 s
> 0 (
s
> 0 (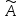 s
< 0) говорят о положительной
(отрицательной) или правосторонней
(левосторонней) асимметрии.
s
< 0) говорят о положительной
(отрицательной) или правосторонней
(левосторонней) асимметрии.
Эксцессом вариационного ряда называется число
Эксцесс
является показателем крутости кривой
распределения вариационного ряда
по сравнению с нормальным распределением,
дисперсия которого равна
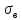 .
При
.
При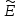 x= 0 распределение нормальное. Если
x= 0 распределение нормальное. Если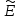 x> 0,то кривая распределения
имеет более острую вершину, чем при
нормальном распределении, если
x> 0,то кривая распределения
имеет более острую вершину, чем при
нормальном распределении, если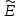 x< 0 - более плоскую.
x< 0 - более плоскую.
Пример 13.2. Вычислить коэффициент асимметрии и эксцесс распределения напряжения тока в электросети для примера 11.1.
Решение. Сначала находим центральные моменты третьего и четвертого порядков:
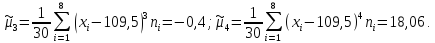
Тогда
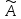 s=
s=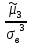 =
= = -0,9;
= -0,9;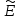 x=
x=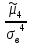 - 3 =
- 3 =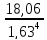 - 3 = - 0,44
- 3 = - 0,44
Поскольку найденные показатели близки к нулю, то можно сделать вывод, что рассматриваемое в примере 11.1 распределение по асимметрии и крутости приближается к нормальной кривой.
Вычисление выборочной средней и дисперсии можно упростить, если использовать не первоначальные варианты xi, а новые варианты
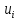 =
=

где С и k- специально подобранные постоянные. Тогда согласно свойствам средней арифметической и дисперсии
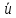 =
=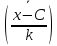 =
=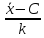 ,
следовательно
,
следовательно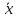 =к
=к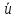 +С ,
+С ,
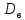 (u)
=
(u)
=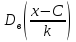 =
=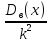 ,
следовательно
,
следовательно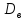 (x)
= k2Dв(u).
(x)
= k2Dв(u).
Данный метод дает существенное упрощение в случае больших значений xi . В качестве постояннойк рекомендуется брать величину интервала поx, а в качествеС - варианту, имеющую наибольшую частоту (середину интервала, имеющего наибольшую частоту).
