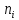- •3. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Свойства вероятности.
- •4.Элементы комбинаторики и схемы выбора.
- •5. Геометрическая вероятность. Свойства вероятности.
- •7. Формула полной вероятности и формула Байеса.
- •8. Схема незовисимых испытаний Бернулли,формула Бернулли.Общая теорема о повторении опытов.
- •9. Общая теорема о повторении опытов. Наиболее вероятное число успехов в схеме Бернулли. Номер первого успешного испытания.
- •10. Предельные теоремы в схеме Бернулли. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
- •11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Закон больших чисел в форме Бернулли.
- •12. Случайные величины и распределения вероятностей. Свойства функции распределения вероятностей.
- •13.Классификация случайных величин. Дискретные распределения (примеры основных распределений)
- •I.Дискретные распределения
- •14. .Классификация случайных величин. Абсолютно непрерывные распределения(примеры основных распределений).
- •I. . Абсолютно непрерывные распределения.
- •15.Нормальное распределение и его свойства.
- •16.Основные распределения случайных величин, применяемые в статистике.
- •17.Мат.Ожидание и его свойства.
- •18.Дисперсия и её свойства
- •20 Числовые характеристики системы двух случайных величин.Ковариация.
- •19.Мода,медиана,моменты,ассиметрия,эксцесс
- •21.Числовые характеристики системы двух случайных величин .Коэффициент корреляции.
- •22.Определение случайной последовательности . Определение сходимости по вероятности .Неравенство Маркова. Неравенство Чебышева.
- •24.Центральная предельная теорема для одинаково распределенных независимых слагаемых. (цпт)
- •25.Определение и описание случайного процесса
- •26.Статистические средние характеристики случайных процессов(сп).
- •27.Стационарные случайные процессы(сп)
- •28.Предмет мат. Статистики
- •29.Средние величины
- •30. Показатели вариации, моменты.
- •31. Статистические оценки параметров распределения. Методы нахождения оценок.
- •32.Метод моментов.
- •34.Интервальные оценки.
34.Интервальные оценки.
Интервальной называют оценку, которая определяется двумя числами - концами интервала, покрывающего оцениваемый параметр.
Доверительным
называют интервал (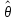 -δ,
-δ,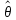 +δ),
который покрывает (содержит) неизвестный
параметр θ с заданнойнадежностью
{доверительной вероятностью) γ, то
естьp(|
+δ),
который покрывает (содержит) неизвестный
параметр θ с заданнойнадежностью
{доверительной вероятностью) γ, то
естьp(|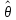 -θ|<δ) =γ.
-θ|<δ) =γ.
При этом δ называютточностью оценки.
Следует
обратить внимание на то, что границы
интервала и его величина находятся по
выборочным данным и поэтому являются
случайными величинами в отличие от
оцениваемого параметра θ- величины неслучайной, поэтому
говорят, что интервал (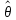 -δ,
-δ,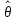 +δ)
«покрывает» («накрывает»), а не
«содержит» истинное значение θ.
+δ)
«покрывает» («накрывает»), а не
«содержит» истинное значение θ.
Величина доверительного интервала существенно зависит от объема выборки п (уменьшается с ростомп ) и значения доверительной вероятности γ (увеличивается с приближением γ к единице).
Интервальной
оценкой с надежностью γ математического
ожидания а нормально распределенного
количественного признака ξ, по
выборочной средней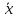 при известном среднем квадратическом
отклонении σ генеральной совокупности
служит доверительный интервал
при известном среднем квадратическом
отклонении σ генеральной совокупности
служит доверительный интервал
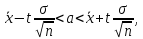
где
δ =
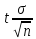 - точность оценки,п - объем выборки,t - значение
- точность оценки,п - объем выборки,t - значение
аргумента
функции Лапласа Ф(t), при
котором Ф(t) =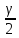 .
.
При неизвестном среднем квадратическом отклонении σ используют интервал:
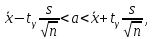
где
s=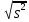 - «исправленное» выборочное среднее
квадратическое отклонение,
- «исправленное» выборочное среднее
квадратическое отклонение,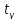 находят по таблице приложения 4 по
заданнымп и γ.
находят по таблице приложения 4 по
заданнымп и γ.
Интервальной оценкой с надежностью γ среднего квадратического отклонения σнормально распределенного количественного признака ξ по «исправленному» выборочному среднему квадратическому отклонениюs служит доверительный интервал
s(1- q) < σ < s(1 + q) при q < 1,
0 < σ < s(1 + q) при q > 1,
где q находят по таблице приложения 5 по заданнымnи γ.
Первый из рассмотренных интервалов строится на основе следствия из теоремы Ляпунова (центральная предельная теорема):
Р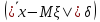 = 2Ф
= 2Ф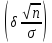 =γ.
=γ.
Для
определения необходимого объема выборки,
при котором с вероятностью γ можно
утверждать, что для нормально распределенной
величины выборочное среднее
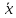 отличается от генеральной средней
отличается от генеральной средней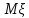 по абсолютной величине меньше чем на
по абсолютной величине меньше чем на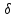 ,
пользуются формулой:
,
пользуются формулой:
n
=
 .
.
Пример 15.1. Из генеральной совокупности извлечена выборка объемап = 25 :
|
|
4 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
1 |
6 |
3 |
3 |
7 |
3 |
2 |
Найти:
1) несмещенную оценку генеральной средней;
2) несмещенную оценку генеральной дисперсии.
Решение.
I) Как было рассмотрено выше, несмещенной оценкой генеральной средней является выборочная средняя:
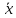 =
=
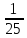 (4∙1 + 6∙6 + 7∙3 + 8∙3 + 9∙7 + 10∙3 + 11∙2) = 8.
(4∙1 + 6∙6 + 7∙3 + 8∙3 + 9∙7 + 10∙3 + 11∙2) = 8.
2) Несмещенной оценкой генеральной дисперсии является «исправленная» выборочная дисперсия:
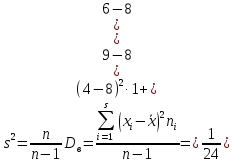
Пример
15.2. Найти доверительный интервал
для оценки математического ожиданияа и среднего квадратичного отклонения
σ нормально распределенного признака
с надежностью γ =0,99, зная выборочную
среднюю = 10,5, объем выборкиn= 25 и
выборочное «исправленное» среднее
квадратическое отклонениеs= 3.
= 10,5, объем выборкиn= 25 и
выборочное «исправленное» среднее
квадратическое отклонениеs= 3.
Решение. Доверительный интервал для математического ожидания имеет вид
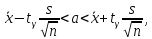
Все величины, кроме tγ, известны. Найдемtγпoтаблице приложения 4,tγ= 2,797. Тогда
10,5-2,797
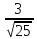 <а < 10,5 + 2,797
<а < 10,5 + 2,797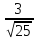 .
.
Окончательно имеем
-8,82 < а < 12,18.
Найдем доверительный интервал для среднего квадратического отклонения
s(1- q) < σ < s(1 + q) при q < 1,
0 < σ < s(1 + q) при q > 1.
Сначала определим параметр q по таблице приложения 5. При
n= 25,γ = 0,99 параметрq = 0,49. Тогда получаем доверительный интервал
3(1-0,49) <σ < 3(1+0,49).
После вычислений
1,53 < σ < 4,47.
Пример 15.3. Найти минимальный объем выборки, при котором с надежностью 0,95 точность оценки математического ожиданияа генеральной совокупности по выборочной средней равнаδ= 0,3, если известно среднее квадратическое отклонение σ = 1,2 нормально распределенной генеральной совокупности.
Решение.Воспользуемся формулой, определяющей
точность оценки математического ожидния
генеральной совокупности по выборочной
средней:δ = t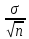 . Отсюда
. Отсюда
n
=
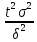 .
.
Определим
величину tиз условия
Ф(t) =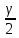 ,
то есть
,
то есть
Ф(t)
=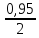 = 0,475. По таблице приложения 2 найдемt
= 1,96. Тогда
= 0,475. По таблице приложения 2 найдемt
= 1,96. Тогда
n
=
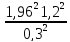 = 61.
= 61.