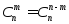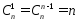1. Интуитивные представления о случайных событиях

Предметом теории вероятности является математический анализ случайных явлений. Под случайными явлениями понимаются явления с неопределенным исходом. Невозможность предсказать заранее исход- это основное, что отличает случайные явления от детерминированного (явление с определенным исходом).

Пример СЯ: при подбрасывании монеты возможны два исхода.

Необходимо подчеркнуть, что ТВ занимается изучением не любых событий, которые в житейской практике называют случайными, а только тех из них, которые обладают следующими свойствами:

1. Неопределенность исхода единичного эксперимента (монета, кубик)

2. Возможность неограниченного повторения в одинаковых условиях.

ТВ не занимается изучением уникальных событий ; событий, которые невозможно повторить в неизменных условиях; событий, результаты которых зависят от субъективных суждений этого или иного лица (сдача экзамена в принципе зависит от преподавателя; результат выборов)

3. Стабилизация относительной частоты.

При неограниченном числе повторений случайных экспериментов относительная частота каждого исхода стабилизируется около величины приблизительно равной теоретической вероятности этого исхода. Это свойство можно обосновать законом больших чисел.

2. Пространство элементарных исходов (пэи). Соотношения между событиями и операции над ними.

О1. ПЭИ (событий) обозначается Ω называется множество, содержащее все возможные результаты данного случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называются элементарными событиями (ЭИ) и обозначаются ω с индексом или без.

Ω = {ω₁, ω₂, …, ω_n, …}

Пример: Подбрасывается игральный кубик

Ω={1,2,3,4,5,6}

О2. Событием называется производное подмножество ПЭИ

События будем обозначать А,В,С,… Говорят, что произошло событие А (А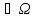) если в эксперименте произошел один из ЭИ, входящих в А.

Пример: подбрасываем игральные кости.

Пусть событие А= «выпало четное число очков», тогда А={2,4,6}

О3. Событие, которое обязательно происходит в данном опыте, называют достоверным и обозначают Ω, т.к. оно состоит из всех ЭИ

О4. События, которые никогда не происходят в данном опыте, обозначают ∅ и называют невозможным

О5. Пересечением (произведением) двух событий А и В называют событие С (С = А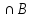, С = А*В), происходящее тогда и только тогда когда одновременно происходят события А и В, т.е. событие, состоящее из ЭИ, принадлежащих и событию А, и событию В

О6. События А и В называют несовместными или непересекающимися, если их пересечение является невозможным событием

А*В=

О7. Объединением (суммой) двух событий А и В называется событие С, происходящее тогда и только тогда, когда происходит хотябы одно из событий А или В

С = А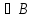С = А+В

Знак «+» обычно используют, когда заведомо известно , что А и В – несовместимы.

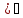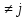О8. События А₁, А₂, … , А_n называют попарно несовместными, если А_iA_j , i , ij=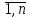, и несовместными в совокупности, если А₁*А_2*…*А_n = ∅

О9. Событие называют противоположным к событию А (дополнением А), если оно происходит тогда и только тогда, когда не происходит А.

О10. Событие А включено в событие В (влечет В) А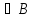, если при наступлении А обязательно наступает В.

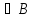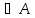
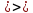О11. События А и В называют равносильными (равными), если Аи ВА=В

О12. События А₁, А₂, … , А_n образуют полную группу событий, если:

1.События попарно несовместны

2.Сумма этих событий есть достоверное событие А1*А2*…*А_n = Ω

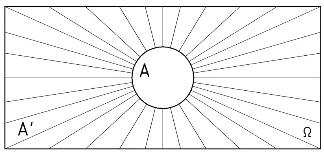
Введенные определения могут быть проиллюстрированы на диаграммах Эйлера:

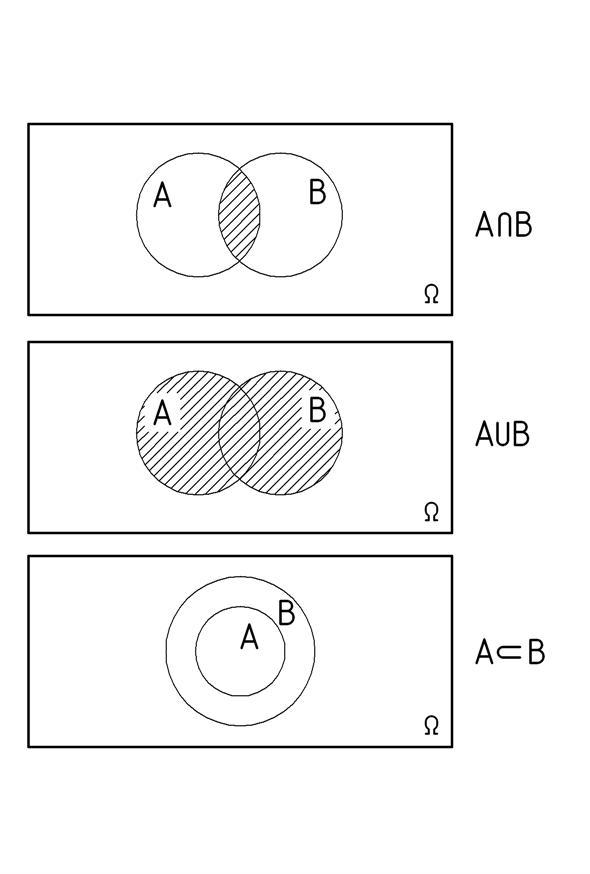
Свойства и операции над событиями:

1. Коммутативность сумм (произведений)

А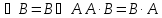

2. Ассоциативность суммы (произведения)

(А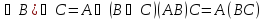

3. Дистрибутивность относительно сложения

(А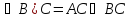

4. А

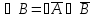
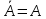5. двойное дополнение

6. 

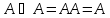
7. Законы Моргана

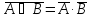
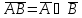
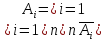
3. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Свойства вероятности.

Предположим, что мы имеем дело с дискретным пространством элементарных исходов (т.е. пространством, состоящим из конечного или счетного числа элементов)

Ω = {ω₁ , ω₂ … ω_n …}

Счетное – если его элементы можно «пересчитать» с помощью множества натуральных чисел.

Поставим каждому элементу 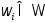в соответствие некоторый «вес» (p(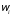)) удовлетворяющий следующим условиям:

1. p(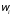)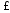1 неотрицательность

p(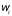)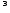0

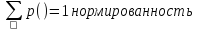
О1. Число p(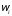) назовем вероятностью элементарных исходов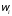 , тогда вероятность любого события А 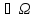определим по формуле:

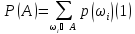
Т.е. вероятность события А равна сумме вероятностей элементарных исходов, входящих в А.

Из (1) следуют следующие свойства:

1. Р() = 0

2. Р(Ω) = 1

3. Р(А

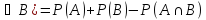
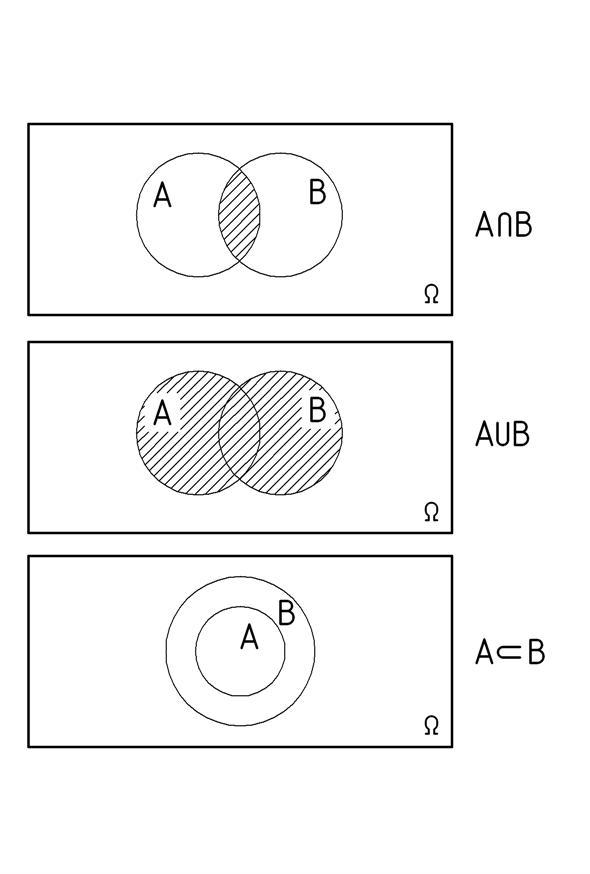
4. Если АВ = то Р(А+В) = Р(А) + Р(В)

5. Р(

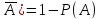
Р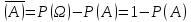

Классическое определение вероятности

Предположим, что:

1. Пространство элементарных исходов состоит из n числа элементов : Ω = {ω₁ , ω₂ … ω_n }

2. все элементарные исходы равновозможны

Поэтому:

При выполнении перечисленных предположений говорят, что эксперимент удовлетворяет классической вероятностной модели.

Рассмотрим в этой модели событие А, состоящее из ω_i

А = {ω₁ , ω₂ … ω_к }

Тогда вероятность события А:

Р(А) = р(ω₁) + р(ω₂) +…+ р(ω_к) =

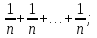
О2. (классическое определение вероятностей)

Если эксперимент удовлетворяет классической вероятностной модели, то вероятность события А рассчитывают по формуле:

Р(А) = 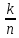эта формула читается так:

«Вероятность события А равна отношению числа исходов (k), благоприятствующих А, к общему числу исходов(n) »

Пример: монета подбрасывается 2 раза. Найти вероятность того, что орел выпадет хотя бы 1 раз .

Ω = {o,o; o,p; p,o; p,p }

А = ''орел появился хотя бы 1 раз ''

А = { o,o; o,p; p,o } Р(А) =

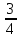
4.Элементы комбинаторики и схемы выбора.

Основные правила:

1. Правило суммы

Если объект А может быть выбран m-способами, а объект В может быть выбран другими n-способами, то выбор одного элемента А или В из объединенной совокупности может быть осуществлен m+n-способами.

2. Правило произведения

Если объект А может быть выбран m-способами, и после каждого такого выбора объект В может быть выбран n-способами, то выбор пары объектов А и В (в указанном порядке) из объединенной совокупности может быть осуществлен m*n-способами

Пример: На карточках имеются буквы слова «математика». Сколькими способами можно получить последовательность «ма», выбирая последовательно наугад по 2 карточки.

М – 2, а – 3, ма – 2*3=6 способов

Элементы комбинаторики:

О1. Результат выбора m элементов из группы, содержащей n элементов, будем называть выборкой из n по m. Если при этом элемент после выбора снова возвращается в группу, то выборку называют выборкой с возвращением. Если же выбранные элементы не участвуют в дальнейшем выборе, то выборку называют выборкой без возвращения.

О2. Выборку, в которой не учитывается порядок выбора элементов, называют сочетанием, а выборку, в которой учитывается порядок выбора элементов, - размещением. При этом, если рассматривать выборку в возвращением, то сочетание (размещение) называют сочетанием (размещением) с повторениями.

О3. Размещение без повторений из n элементов по n элементов называют перестановкой из n элементов.

Пусть есть элементы a,b,c

●Число перестановок из n элементов:

P_n = n! P₃ = 3! = 6 (abc, bac, acb, cab, bca)

●Число всех возможных размещений из n по m элементов:

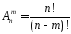
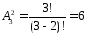(ab, ba, bc, cb, ac,ca)

●Число размещений с повторениями:

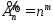
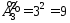(ab, ba, bc, cb, ac, ca, aa, bb, cc)

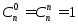
●Число всех возможных сочетаний:

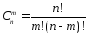
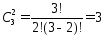(ab, bc, ca)

●Число сочетаний с повторениями:

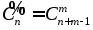
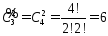(ab, bc, ac, aa, bb, cc)

1. 1! = 1

2. 0! = 1

3. 

   

4. 

5.