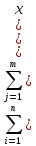- •3. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Свойства вероятности.
- •4.Элементы комбинаторики и схемы выбора.
- •5. Геометрическая вероятность. Свойства вероятности.
- •7. Формула полной вероятности и формула Байеса.
- •8. Схема незовисимых испытаний Бернулли,формула Бернулли.Общая теорема о повторении опытов.
- •9. Общая теорема о повторении опытов. Наиболее вероятное число успехов в схеме Бернулли. Номер первого успешного испытания.
- •10. Предельные теоремы в схеме Бернулли. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
- •11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Закон больших чисел в форме Бернулли.
- •12. Случайные величины и распределения вероятностей. Свойства функции распределения вероятностей.
- •13.Классификация случайных величин. Дискретные распределения (примеры основных распределений)
- •I.Дискретные распределения
- •14. .Классификация случайных величин. Абсолютно непрерывные распределения(примеры основных распределений).
- •I. . Абсолютно непрерывные распределения.
- •15.Нормальное распределение и его свойства.
- •16.Основные распределения случайных величин, применяемые в статистике.
- •17.Мат.Ожидание и его свойства.
- •18.Дисперсия и её свойства
- •20 Числовые характеристики системы двух случайных величин.Ковариация.
- •19.Мода,медиана,моменты,ассиметрия,эксцесс
- •21.Числовые характеристики системы двух случайных величин .Коэффициент корреляции.
- •22.Определение случайной последовательности . Определение сходимости по вероятности .Неравенство Маркова. Неравенство Чебышева.
- •24.Центральная предельная теорема для одинаково распределенных независимых слагаемых. (цпт)
- •25.Определение и описание случайного процесса
- •26.Статистические средние характеристики случайных процессов(сп).
- •27.Стационарные случайные процессы(сп)
- •28.Предмет мат. Статистики
- •29.Средние величины
- •30. Показатели вариации, моменты.
- •31. Статистические оценки параметров распределения. Методы нахождения оценок.
- •32.Метод моментов.
- •34.Интервальные оценки.
19.Мода,медиана,моменты,ассиметрия,эксцесс
Модой
дискретной СВ называется её наиболее
вероятное значение,модой непрерывной
СВ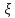 -значение аргументаx,при котором её плотность распределения
-значение аргументаx,при котором её плотность распределения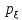 (x)
максимальна.Медианой СВ
(x)
максимальна.Медианой СВ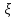 называется значение аргументаx, при котором
называется значение аргументаx, при котором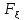 (x)=0,5.Начальным
моментом порядкаNСВ
(x)=0,5.Начальным
моментом порядкаNСВ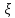 называется
называется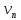 =M
=M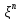 ,ацентральным моментом порядкаN-
,ацентральным моментом порядкаN-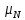 =M
=M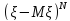 .В
случае многомерных СВсмешанным
начальным моментом порядка NСВ
.В
случае многомерных СВсмешанным
начальным моментом порядка NСВ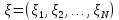 называетсяM
называетсяM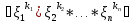 ,где
,где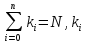 -целые
неотрицательные числа .Смешанным
центральным моментом порядкаNназывается
-целые
неотрицательные числа .Смешанным
центральным моментом порядкаNназывается
M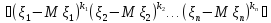 .
.
Основные свойства дисперсии:
дисперсия любой случайной величины неотрицательна, Dx0;
дисперсия константы равна нулю, Dc=0;
для произвольной константы D(cx) =c2D(x);
дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x±h) =D(x) +D(h).
Моменты
В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.
Начальным моментом k-го порядка случайной величиныxназывается математическое ожиданиеk-й степени случайной величиныx, т.е.ak=Mxk.
Центральным моментом k-го порядка случайной величиныxназывается величинаmk, определяемая формулойmk=M(x-Mx)k.
Заметим, что математическое ожидание случайной величины - начальный момент первого порядка, a1 =Mx, а дисперсия - центральный момент второго порядка,
a2 =Mx2 =M(x-Mx)2 =Dx.
Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:
m2=a2-a12,m3 =a3 - 3a2a1 + 2a13.
Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x=Mx, то все ее центральные моменты нечетного порядка равны нулю.
Асимметрия
В теории вероятностей и в математической статистике в качестве меры асимметрии распределения является коэффициент асимметрии, который определяется формулой ,
где m3 - центральный момент третьего порядка, - среднеквадратичное отклонение.
Эксцесс
Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины x, от нормального распределения, является эксцесс.
Эксцесс g случайной величины x определяется равенством .
У нормального распределения, естественно, g= 0. Еслиg(x) > 0, то это означает, что график плотности вероятностейpx(x) сильнее “заострен”, чем у нормального распределения, если жеg(x) < 0, то “заостренность” графикаpx(x) меньше, чем у нормального распределения.
21.Числовые характеристики системы двух случайных величин .Коэффициент корреляции.
Коэффициентом корреляции двух случайных величин называется: r(ξ1, ξ2)=сov(ξ1, ξ 2)/ σ ξ1*σξ2),σ ξ1,σξ2≠0-среднее квадратичное отклонение случайных величин.
Свойства :
r(ξ1,ξ1)=1
r(c* ξ1, ξ2)=c* сov(ξ1, ξ 2)/ σc ξ1*σξ2)=c* сov(ξ1, ξ 2)/c*( σ ξ1*σξ2)=r(ξ1,ξ2) т.е. коэффициент корреляции безразмерная величина.
r(ξ1,ξ2)=r(ξ2,ξ1)
Если СВ ξ1, ξ 2 независимы, то r(ξ1,ξ2)=0. Обратное верно не всегда, т.е. еслиr(ξ1,ξ2)=0 , то СВ ξ1, ξ 2 могут быть как зависимыми так и независимыми. Исключения составляют случаи, когда ξ1 и ξ 2 имеют нормальное распределение в этом случае еслиr(ξ1,ξ2)=0
То мы можем сделать вывод что ξ1 и ξ 2 независимы.
СВ (ξ1, ξ2) называются не коррелированными, если r(ξ1,ξ2)=0. Т. О из независимости коррелированность следует всегда., а из коррелированности независимость при условии, что СВ имеет нормальное распределение.
І r(ξ1,ξ2)І ≤1.Коэффициент
равен ±1 тогда и только тогда когда СВ
линейно зависимы. Іr(ξ1,ξ2)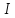 =1
следует ξ1=a+b*ξ2 причемr=1 приb›0
иr=-1 приb‹0.
Пусть имеются следующие графики на
которых точками отмечены пары значений
СВ (ξ1,ξ2).
=1
следует ξ1=a+b*ξ2 причемr=1 приb›0
иr=-1 приb‹0.
Пусть имеются следующие графики на
которых точками отмечены пары значений
СВ (ξ1,ξ2).
|
А |
б |
в |
|
Г | ||
Графики а,б,в,г называются полями корреляции.
Тогда сравнивая представленных четыре случая можно сделать вывод что в а,б, в наблюдается линейная зависимость ξ1, ξ2 причем к случаю в все точки лежат на одной прямой поэтому зависимость строго зависимая. Если сравнивать а и б, то во-первых в случае а мы видим прямую линейную зависимость а в случае б обратную прямую зависимость . во-вторых т. К. точки на графике б сконцентрированы теснее чем на графике а, то линейная зависимость б более тесная чем в а. в случае г по графику наблюдений вывод о зависимости не может быть сделан.выводы по коэффициенту корреляции:
По значению можно сделать следующие выводы:
Rхарактеризует степень линейной зависимости . , чем ближеrк ±1 тем более тесная линейная зависимость между ξ1, ξ2 .
Если r=±1 то зависимость строго линейная .
Если r›0 то говорят о прямой корреляции между СВ т.е . при возрастании значений одной СВ , значения другой так же растут. Еслиr‹0 то говорят об обратной корреляции т.е. при возрастании значений одной СВ , значения другой убывают. еслиr=0 или ІrІ близок к 0 ,то можно сделать вывод об отсутствии линейной зависимости меду СВ , нелинейная зависимость при этом моет быть даже очень тесной . Т.о. для случая , изображенного на графике б), г) ІrІ близок к 0 в случае в) имеет 100% линейную зависимость . в б)r‹0 . В а)r›0 причем Іrб)І› Іrа)І
Числовые характеристики: характеристикой
зависимости между СВ Х и У служит мат
ожидание произведения отклонений Х и
У от их центров распределений, которое
называется корреляционным моментом
или ковариацией. Используют формулу: