10. Предельные теоремы в схеме Бернулли. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.

При больших значениях n и m вычисление вероятностей Pn(m) превращается в технически сложную задачу.

Задача усложняется при расчете вероятности вида: 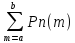В этих случаях пользуются приближенными асимптотическими формулами.

ТЕОРЕМА 1.(локальная предельная теорема Муавра-Лапласа):

Вероятность того, что в n-независимых испытаниях событие А наступит ровно m раз определяется по формуле: Pn(m)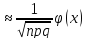- (1), где,x=,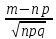

где p (0<p<1)- вероятность наступления A в отдельном испытании. q=1-p.

Замечание: равенство (1) тем точнее, чем больше n и ближе p к 0.5.

Свойства:

1. Значение можно найти по таблицам приложения.

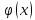2. –четная, .

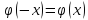3. Монотонно убывающая при x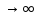, 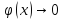. (она очень быстро стремиться), причем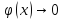очень быстро, будем считать что приx,

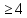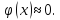
Пример: найти вер-ть того, что при 600бросаниях игрального кубика выпадет ровно 120 шестерок.

n=600, m120, p=1/6, q=5/6.

P600(120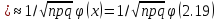= 0.004

X=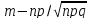=2.19

ТЕОРЕМА 2.(интегральная предельная теорема Муавра-Лапласа):

Пусть вероятность появления события A в каждом из n независимых испытаний равна p (0<p<1). Тогда вер-ть того ,что в n-независимых испытаниях событие A появится от m₁ до m₂ раз (m₁≥ m₂) выражается формулой:

Pn(m₁≤m≤m₂)= Pn(m₁;m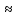₂)Ф(x₁)- Ф(x₂),

где Ф(x)= 1/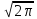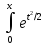dt

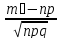x₁=,x₂=.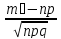

Свойства функции Ф(x):

1. Значение можно найти по таблицам приложения.

2. Эта функция нечетная, т.е. Ф(-x)=-Ф(x).

3. Монотонно возрастающая, при 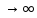x, Ф(x)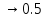, причем стремится быстро. Считают, что уже при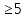x, Ф(x)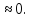

Пример: определить вероятность того, что число выпавших шестерок заключено в интервале от 90 до 120.

P600(90≤m≤120)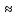Ф(2.19)- Ф(-1.1) =Ф(2.19)+ Ф(1.1)=0.85007

x₁=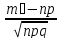=x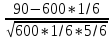=-1.10, x₂=2.19.

11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Закон больших чисел в форме Бернулли.

Закон больших чисел в форме Бернулли.

Пусть теоретическая вероятность наступления события A в каждом из n-испытаний равна p, тогда вероятность того, что относительная частота наступления события A отклонится от вероятности р по абсолютной величине меньше чем на 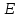приблизительно равна:

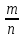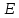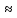P(|-p|<)2Ф()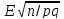

Пример: вероятность того, что деталь не стандартная равна 0.2. Сколько деталей нужно отобрать, чтобы с вероятностью 0.97 можно было утверждать, что относительная частота появления нестандартных деталей отклонится от вероятности p=0.2 по абсолютной величине не более чем на 0.01.

P=0.2, q=0.8, n-? P(|m/n-0.2|≤0.01)=0.97)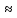2Ф()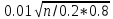

m/n – относительная частота появления нестандартных деталей.

Ф(0.01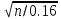)=0.485,n= 2.17*2.17*0.16/0.01*0.01

0.01= 2.17

В случаях, когда число испытаний n больше, а вероятность успеха в каждом испытании p пользуются теоремой Пуассона.

Теорема Пуассона.

Пусть вероятность появления события A в каждом из n-независимых испытаний равна p, причем 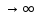n ,n 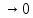, тогда справедлива следующая формула:

Pn(m)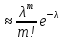где λ=np.

На практике эта теорема дает хорошее приближение, когда λ≤10

Пример: вероятность выпуска бракованного сверла равна 0.015ю Найти вероятность того, что в партии из 100 изделий нет ни одного бракованного.

P=0.015, n= 100, λ=100*0.015=15

P100(0)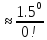*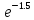==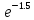 0.22313