Раздел XII: определенный интеграл.

12.1. Определение и свойства:

О

пределение:

Конечный предел интегральной суммы функции наназывается определенным интегралом от этой функции на.

Т.о. , где.

Теорема(формула Ньютона-Лейбница): Определенный интеграл от непрерывной функции равен разности двух значений любой первообразной подынтегральной функции, взятых при верхнем и нижнем пределах интегрирования:.

Основные свойства определенного интеграла:

1) ;

2) ;

3) - свойство аддитивности

4) Если на , где, то и;

5) Интегрирование неравенств:

Если на , где, то и;

6) Об оценке определенного интеграла:

Если - наименьшее,- наибольшее значения функциина, то

;

7) ;

8) Теорема о среднем: , где

9) .

12.2. Методы вычисления определенного интеграла:

- Непосредственное интегрирование (применение формулы Ньютона-Лейбница);

- Замена переменной интегрирования: . Здесь не возвращаются к исходной переменной, но сразу вводят новые пределы интегрирования.

- Интегрирование по частям: если - непрерывно-дифференцируемы на, то.

Все замечания, сделанные к аналогичному методу в неопределенном интеграле остаются справедливыми.- Определенный интеграл на отрезке симметричном нулю от нечетной функции равен нулю, от четной – двум интегралам, взятым по половине исходного отрезка интегрирования:

.

12.3. Несобственные интегралы:

Первого рода:

Пусть - непрерывна наили на: 1.или,

если эти пределы существуют и конечны, то соответствующий несобственный интеграл называется сходящимся, если не существует или равен бесконечности, то расходящимся.

2. , где- любая точка оси.

Полный интеграл сходится, тогда и только тогда, когда сходится каждый из составляющих его интегралов.

Второго рода:

Пусть - непрерывна вили:

1. или,

если эти пределы существуют и конечны, то соответствующий несобственный интеграл называется сходящимся, если не существует или равен бесконечности, то расходящимся.

2., где- внутренняя точка бесконечного разрыва.

Такой несобственные интеграл, сходится тогда и только тогда, когда сходятся оба составляющих его интеграла.

12.4 Применения определенного интеграла:

1. Вычисление площадей плоских фигур:

• - площадь криволинейной трапеции, где;

• - площадь криволинейной трапеции, где;

• - площадь фигуры, где,;

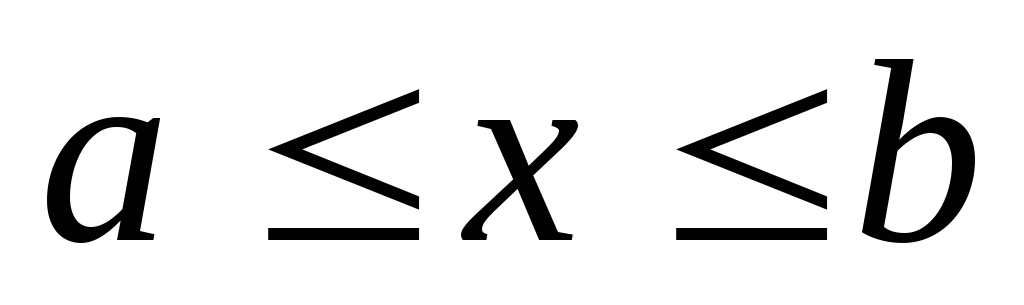• -площадь фигуры, где основная кривая задана как,

где ,- непрерывно-дифференцируемы на;

• - площадь фигуры, где основная кривая задана в п.с.к. уравнением,.

2.Вычисление длин дуг плоских кривых:

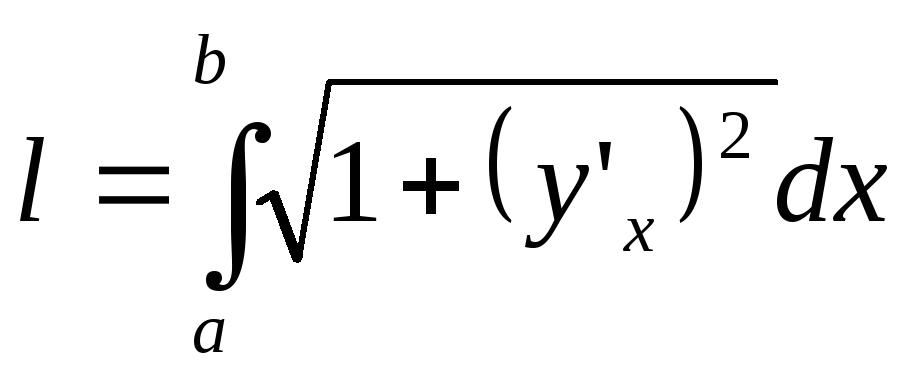• - формула вычисления длины дуги, заданной явно, где- непрерывно-дифференцируема на

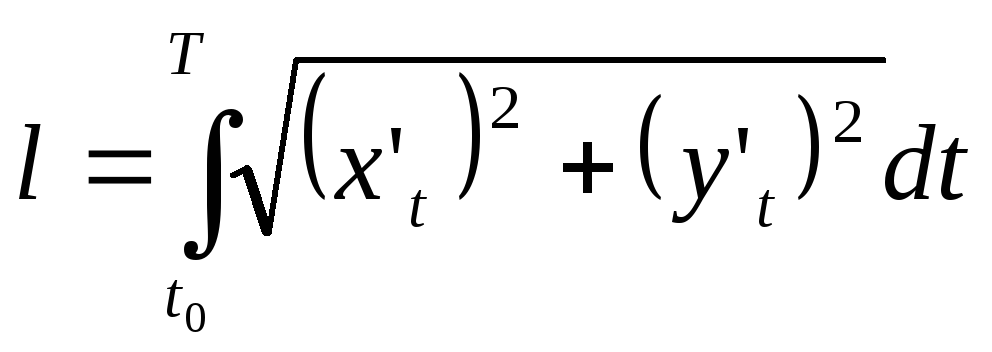• - для дуги, заданной параметрически, где- непрерывно-дифференцируемы на.

• - для дуги кривой в п.с.к., гдеи- непрерывно-дифференцируема на.

3. Вычисление площадей поверхностей вращения:

• - вокруг оси;

• - вокруг оси;

• - для кривой, заданной параметрически;

• - для кривой в п.с.к.

4. Вычисление объемов тел вращения:

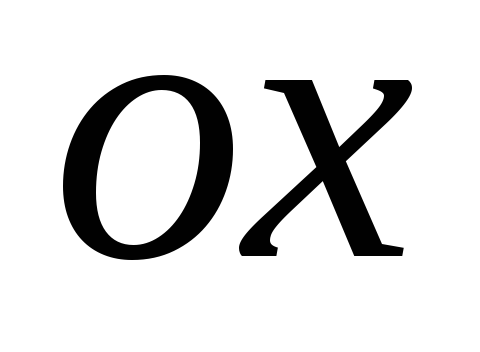• - вокруг оси;

• - вокруг оси.

5. Физические приложения определенного интеграла:

• - формула нахождения пути по скорости при прямолинейном движении;

• - масса неоднородного стержня длиныс заданной линейной плотностью;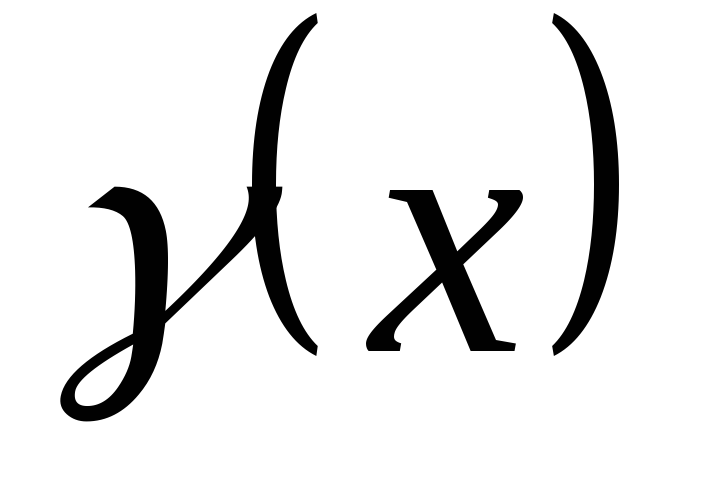

• - угол поворота за отрезок временипри заданной угловой скорости;

• - количество теплоты необходимое для нагревания тела от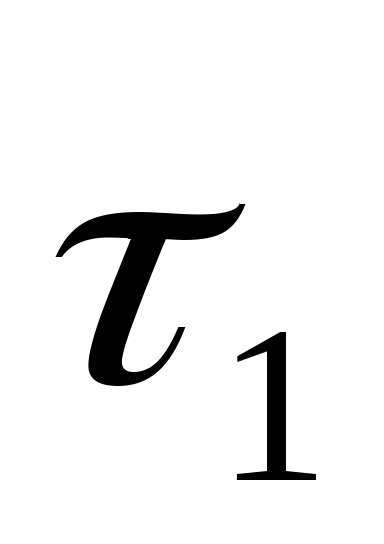допри заданной теплоемкости;

• - количество электричества, протекающего через поперечное сечение проводника за отрезок временипри заданной силе тока;

• - работа переменной силы при прямолинейном перемещении (физический смысл определенного интеграла);

• - формула вычисления давления жидкости на вертикальную пластину.