11.3 Общие методы интегрирования:

1. Непосредственное интегрирование: подинтегральное выражение преобразуют так, чтобы заданный интеграл можно было представить в виде одного или алгебраической суммы нескольких табличных интегралов.

2. Способ подстановки: вводят новую переменную интегрирования, так чтобы интеграл с новой переменной или был бы табличным или брался бы одним из известных способов, т.е..

Алгоритм вычисления:

1. Вводим новую переменную интегрирования .

2. Представляем заданное подынтегральное выражение в переменных 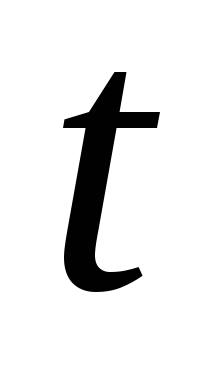и.

3. Берем интеграл с новой переменной.

4. В полученной первообразной заменяем переменную на.

Применяется в случае:

- если , то;

-если , то;

- если , то;

- если , то;

- если - действительные числа,- любое,, то.

3.Интегрирование по частям:

Применяется при интегрировании специально подобранных функций.

- формула интегрирования по частям, где- непрерывно - дифференцируемы при всех рассматриваемых.

Алгоритм нахождения:

1) Разбиваем заданное подынтегральное выражение на два множителяи.

2) Находим и.

3) К заданному интегралу применяем формулу .

Классы функций, интегрируемых по частям:

1 класс:,

Здесь - , где- многочлен любой степени, кроме нуля,- любое ненулевое действительное число.

2 класс:,

Здесь - , где- многочлен любой степени, включая нулевую,- любое ненулевое действительное число.

3 класс:, где- любое ненулевое действительное число.

Здесь выбор безразличен.

Замечания:

1. при нахождении интегралов первого класса формулу интегрирования по частям применяют столько раз, какова степень данного многочлена .

2. Нахождение интегралов третьего класса в итоге сводится к решению уравнения относительно заданного интеграла.

4. Интегрирование рациональных дробей:

Алгоритм нахождения:

- Проверяем, является ли заданная рациональная дробь правильной, если дробь неправильная, то представляем ее в виде суммы целой части и правильной рациональной дроби (для этого в общем случае делим числитель на знаменатель, в частности используем формулы сокращенного умножения)

- Раскладываем правильную рациональную дробь на сумму простейших методом неопределенных коэффициентов.

Определение: правильные рациональные дроби вида

, где- любые действительные числа

, где- любые действительные числа,

, где

, где

называются простейшими дробями 1-4 типов.

Алгоритм представления правильной рац. дроби в виде суммы простейших дробей:

- каждому простому действительному корню знаменателя соответствует одна дробь;

- каждому кратному действительному корню знаменателя соответствуют одна дробьидробь:

- каждой простой паре комплексно-сопряженных корней знаменателя соответствует одна дробь;

- каждой - кратной паре комплексно-сопряженных корней знаменателя соответствуют дробьидробь:

Алгоритм нахождения коэффициентов разложения правильной рац. дроби:

- приводим правую часть разложения к общему знаменателю, получаем тождественное равенство двух дробей с одинаковыми знаменателями;

- отбрасываем эти знаменатели, получаем тождество из числителей;

- в последнем тождестве последовательно придаем значения действительных корней знаменателя исходной дроби, если они есть, а затем нужное число раз сравниваем коэффициенты при одинаковых степенях . Получаем СЛАУ относительно искомых коэффициентов;

- решив СЛАУ, находим коэффициенты и ,значит, само разложение;

- Интегрируем простейшие дроби и, если есть, целую часть:

- интегрируем либо по формуле Остроградского, либо с помощью реккурентных преобразований.

5. Интегрирование функций, рационально зависящих от тригонометрических:

1.

2.

3.

4. ;

5. ;

.

6.

.

6. Интегрирование простейших алгебраических иррациональностей:

1. , где- любые действительные числа,,- любые натуральные числа, составляющие несократимые дроби.

Здесь , где- общий знаменатель дробей;

2. , где

3. , где-любые действительны числа неравные нулю.

4. - выделяем полный квадрат под знаком корня.

5. ;

6. - в числителе получают дифференциал подкоренного выражения;

7. , где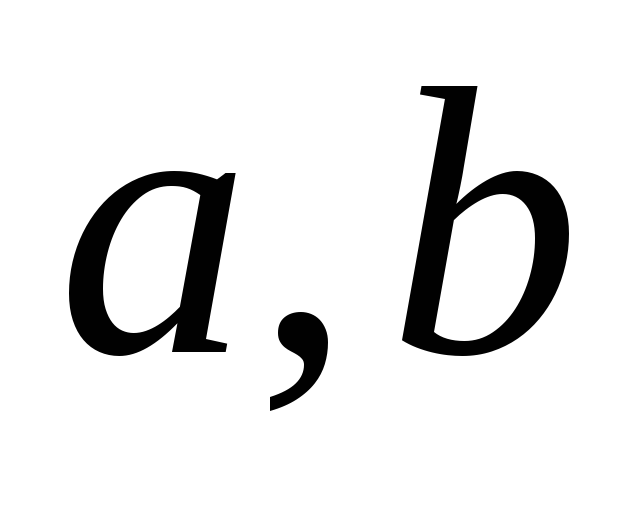- любые неравные нулю действительные числа,- рациональные числа: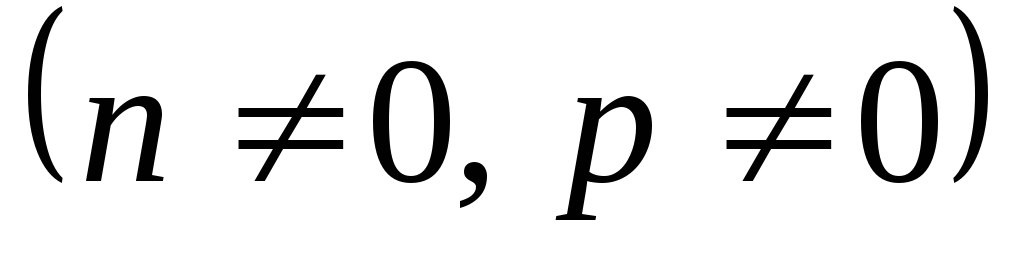

- если - целое, то полагают, где- общий знаменатель дробей;

- если - целое, то, где- знаменатель дроби;

- если - целое, то, где- знаменатель дроби.

Неберущиеся интегралы:

;;;;;;;

.