Раздел VII: кривые, заданные параметрически.
1. Окружность:
, где
.
Э
ллипс:
,
где
.
Астроида:
,
где
.
Ц
иклоида:
,
для первой арки
.
Раздел VIII: нахождение пределов.
8.1. Определение пределов:
Определение 1:
Число
называется пределом функции
в точке
,
если для любого положительного
найдется такое положительное
,
что для всех
,
удовлетворяющих неравенству
выполняется неравенство
Символически:
Геометрический смысл: если для
-
окрестности т.
найдется
-
окрестность
,
что для всех
из этой
-
окрестности соответствующие значения
функции
лежат внутри полосы шириной
,
ограниченной прямыми
.
Определение 2:
Число
называется
пределом функции
при
,
если для любого
существует
,
что при всех
,
удовлетворяющих неравенству
,
справедливо неравенство
.
Обозначение:
.
Г
еометрический
смысл: если существует
,
то для всякого сколь угодно малого
наперед заданного числа
найдется такое свое число
,
,
что, как только становится
,
соответствующие значения функции
попадают в
полосу числа
.
8.2. Бмф и ббф:
Определение:
Функция
называется бесконечно малой (бмф) при
(
),
если
(
).
Теорема:Сумма конечного числа бесконечно малых функции есть функция бесконечно малая.
Теорема:Произведение бмф на ограниченную (она ограничена в сколь угодно малой окрестности точки) есть функция бесконечно малая.
Следствия:
Произведение постоянной на бмф есть бмф;
Произведение двух бмф есть бмф;
Частное от деления бмф на функцию, имеющую предел, отличный от нуля, есть бмф.
Определение:
Если
,
то
- бесконечно большая функция (ббф).
Свойства ббф:
1) Произведение ббф на функцию, имеющую предел, отличный от нуля, есть ббф;
2) Произведение двух ббф есть ббф;
3) Сумма и частное двух ббф есть ббф не всегда.
Теорема:Если
-
ббф в т.
,
то
-
бмф в т.
.
Теорема:Если
-
бмф в т.
,
то
-
ббф в т.
.
Теоремы о пределах:
Если две функции имеют предел, то их сумма также имеет предел, равный сумме пределов этих функций
Если две функции имеют предел, то их произведение также имеет предел, равный произведению пределов этих функций
Если две функции имеют предел, то их частное имеет предел, равный частному пределов этих функций, при условии, что предел делителя отличен от нуля.
Следствия:
Постоянный множитель можно выносить за знак предела.
Теоремы 1и2 остаются справедливыми и в случае любого конечного числа функции, имеющих предел.
8.3. Алгоритм нахождения пределов от алгебраических функций:
1 класс:
Если
-
многочлен
-
ой степени, то:
,
.
2 класс:
Если
-
многочлен
-
ой степени,
-
многочлен
-
степени, то
3 класс:
Если
-
дробь, содержащая иррациональность, то
8.4. Замечательные пределы:
Теорема:
Предел отношения синуса к его аргументу
равен 1, если аргумент стремится к нулю,
т.е.
(первый
замечательный предел).
-второй замечательный предел.
Следствие:
и
.
8.5. Нахождение пределов с использованием бмф:
Пусть
- бмф.
Определение:
Если
,
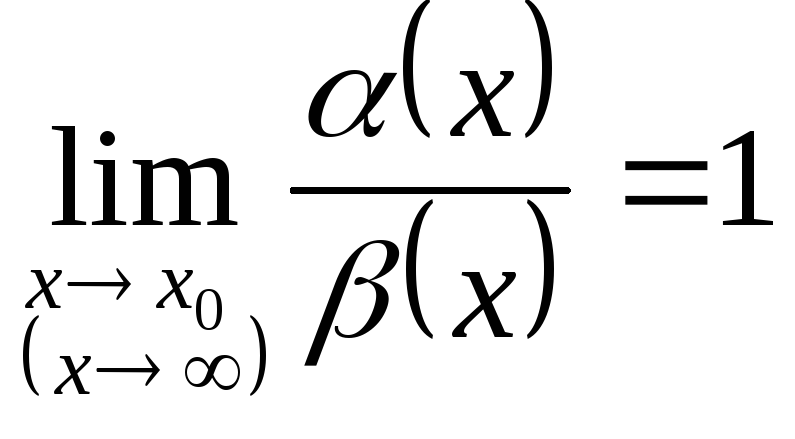то
- называются эквивалентными.
Обозначение:
~
Таблица эквивалентных бмф при
:
1)
~
6)
~
2)
~
~
3)
~
7)
~
4)
~
8)
~
5)
~
~
Основные теоремы об эквивалентных бмф
Теорема 1:
Предел отношения двух бмф не изменится, если хотя бы одну из них заменить ей эквивалентной.
Теорема 2:
Сумма конечного числа бмф, имеющих различный порядок малости эквивалентна слагаемому, имеющему самый низкий порядок малости.
Определение:Слагаемое, которому эквивалентна вся сумма бмф называется главной частью этой суммы.
РАЗДЕЛ IX: ПРОИЗВОДНАЯ ФУНКЦИИ.
9.1. Определение производной. Геометрический и механический смысл:
Определение:
Предел отношения приращения функции к
приращению аргумента при условии, что
приращение аргумента стремится к нулю
произвольным образом, называется
производной функции. Таким образом:
.
Обозначение:
.
Геометрический смысл производной:
Производная функции
,
вычисленная в т.
есть угловой коэффициент касательной,
проведенной к графику функции в точке
с абсциссой
,
т.е.
.
- уравнение касательной к графику функции
в точке
с абсциссой
.
- уравнение нормали к графику функции
в точке
с абсциссой
.
Механический смысл производной:
Производная от пути по времени при
прямолинейном движении точки, есть
истинная или мгновенная скорость
движения
.