14.4. Определение и вычисление тройного интеграла:

П

усть функциянепрерывна в замкнутой облости.

Определение:Конечный предел интегральной суммы функциив областипри условии, чтоиназывается тройным интегралом от этой функции по области, где- диаметр частичной области.

Т.о. .

Вычисление тройных интегралов:

1.В декартовой системе координат:

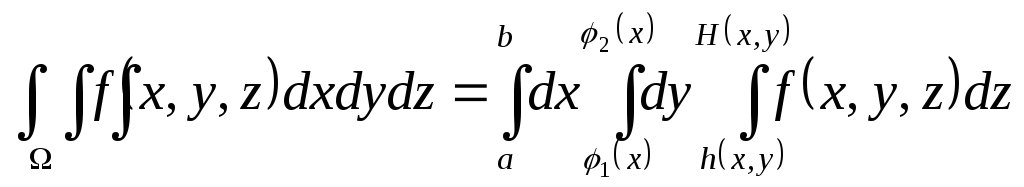
2. В цилиндрической системе координат (ц.с.к.):

Вц.с.к.

,

.

;

Полезно использовать, что .

Тройной интеграл целесообразно вычислять в ц.с.к., если:

- область интегрирования ограничена хотя бы одной из поверхностей(прямой круговой цилиндр),(параболоид вращения),(прямой круговой конус) с;

- область проецируется на плоскостьв круг или любую его часть.

3. В сферической системе координат (с.с.к.):

;

;

.

Тройной целесообразно вычислять в с.с.к., если- шар или его часть.

Полезно использовать, что .

14.5. Применения тройного интеграла:

• - в декартовой системе координат;

• - в цилиндрической системе координат;

• - в сферической системе координат;

• - масса неоднородного телас плотностью;

• ;

;

- статические моменты относительно координатных плоскостей.

• ;;- координаты центра масс;

• ;

; - моменты инерции тела относительно коорд. осей

;

• ;

; - моменты инерции тела относительно коорд. плоскостей

- момент инерции относительно.

Раздел XV: криволиненйные интегралы.

1. Определение криволинейного интеграла по длине дуги и его свойства:

Пустьнепрерывна в каждой точке гладкой дуги.

Определение:

Конечный предел интегральной суммы функции на кривойпри условии, чтоиназывается криволинейным интегралом по длине дуги от функциипо кривой, где

Т.о. .

Основные свойства:

1) ;

2) ;

3) Если в каждой точке дуги , то и;

4) Если в каждой точке дуги , то и;

5) ;

6) , где- длина дуги,- точка дуги.

15.2 Вычисление криволинейных интегралов по длине дуги:

• - в случае явного задания кривой интегрирования;

• - в случае параметрического задания кривой интегрирования;

• - в случае задания кривой интегрирования в п.с.к..

15.3 Применения криволинейного интеграла по длине дуги:

• - длина дуги;

• - масса неоднородной дуги с плотностью;

• ;- стат. моменты дуги относительно коорд. осей;

• ;- координаты центра масс дуги;

• - моменты инерции дуги.

15.4 Криволинейный интеграл по координатам:

- составной криволинейный интеграл.

Пусть - непрерывна в каждой точке гладкой направленной дуги.

Определение:

Конечный предел интегральной суммы функции на кривойпри условии, чтоиназывается криволинейным интегралом по координатеот функциипо кривой, где

Т.о. .

Аналогично .

Основные свойства:

1) ;

2) ;

3) Криволинейные интегралы по координатам, взятые по замкнутому контуру не зависят от выбора на контуре начальной точки, но зависят от направления обхода контура.

Если направление обхода не указано, то полагают, что контур обходится в положительном направлении (такое, при котором точки области, ограниченные контуром, остаются слева).