
- •Чевын м.А.
- •1.7. Формулы Крамера:
- •Раздел II: элементы векторной алгебры.
- •Раздел III: аналитическая геометрия.
- •3.9. Плоскость в пространстве:
- •Раздел VI: уравнения и графики кривых в полярной системе координат.
- •Раздел VII: кривые, заданные параметрически.
- •Раздел VIII: нахождение пределов.
- •8.1. Определение пределов:
- •8.2. Бмф и ббф:
- •8.3. Алгоритм нахождения пределов от алгебраических функций:
- •9.2. Таблица производных:
- •9.3. Логарифмическое дифференцирование:
- •9.4. Дифференцирование функций, заданных неявно:
- •9.5. Дифференцирование функций, заданных параметрически:
- •9.6. Производные высших порядков:
- •9.7. Раскрытие неопределенностей по правилу Лопиталя:
- •9.8. Формула Тейлора:
- •9.10. Общая схема исследования функции и построения ее графика:
- •Раздел X: комплексные числа.
- •10.2. Действия над комплексными числами:
- •Раздел XI: неопределенный интеграл.
- •11.1. Определение и свойства:
- •1.2 Таблица дифференциалов и интегралов:
- •11.3 Общие методы интегрирования:
- •Раздел XII: определенный интеграл.
- •12.1. Определение и свойства:
- •12.2. Методы вычисления определенного интеграла:
- •12.3. Несобственные интегралы:
- •12.4 Применения определенного интеграла:
- •Раздел XIII: дифференциальное исчисление функций нескольких переменных.
- •13.1. Основные понятия:
- •13.2. Частные производные:
- •13.3. Дифференцирование сложных функций:
- •13.4. Дифференцирование неявных функций:
- •13.5. Касательная плоскость и нормаль к поверхности:
- •13.6. Экстремумы функции двух переменных:
- •Раздел XIV: кратные интегралы.
- •14.1. Определение и свойства двойного интеграла:
- •14.3. Применения двойного интеграла:
- •14.4. Определение и вычисление тройного интеграла:
- •14.5. Применения тройного интеграла:
- •Раздел XV: криволиненйные интегралы.
- •15.4 Криволинейный интеграл по координатам:
- •15.5 Вычисление криволинейных интегралов по координатам:
- •15.6 Применения криволинейных интегралов по координатам:
- •Раздел XVI: поверхностные интегралы.
- •16.1. Определение и свойства поверхностого интеграла по площади поверхности:
- •16.4. Определение и свойства поверхностного интеграла по координатам :
- •16.5. Вычисление поверхностных интегралов по координатам:
- •Раздел I: обыкновенные дифференциальные уравнения первого порядка.
- •1.1. Основные понятия:
- •1.3. Дифференциальные уравнения высших порядков:
- •1.4.Системы диффереренциальных уравнений.
- •Раздел II: теория поля.
- •2.2. Векторное поле и его характеристики:
- •Раздел III: ряды.
- •3.3. Знакопеременные ряды:
- •3.4. Степенные ряды:
- •3.5. Ряд Тейлора:
- •3.6. Разложение элементарных функций в ряд по степеням :
- •Раздел IV: теория функций комплексного переменного.
- •4.1. Основные понятия:
- •4.2. Основные элементарные функции:
- •4.3. Определение и свойства контурного интеграла по кривой:
- •4.4. Вычисление контурных интегралов от непрерывной функции комплексного переменного:
- •4.5. Ряды Тейлора и Лорана:
- •4.7. Вычеты:
- •Раздел V:операционное исчисление.
- •5.2. Свойства преобразований Лапласа:
- •5.3. Свертка функций:
- •5.4. Теоремы разложения:
- •5.5 Таблица оригиналов и изображений:
- •Раздел VI: основы теории вероятностей.
- •6.1. Элементы комбинаторики:
- •6.2. Основные понятия теории вероянтостей:
- •6.4. Случайные величины:
- •6.4. Числовые характеристики случайных величин:
- •3) Среднее квадратическое отклонение:
1.3. Дифференциальные уравнения высших порядков:
Дифференциальные уравнения вида
 ,
где
,
где
Для нахождения решения последовательно
интегрируем заданное д.у. по
![]() столько раз, каков порядок уравнения.
столько раз, каков порядок уравнения.
Дифференциальные уравнения вида
 .
.
Для нахождения решения вводим новую
функцию
![]() ,
тогда
,
тогда![]() .
.
Замечание:
- д.у. вида
![]() ,
где
,
где![]()
![]() решаем с помощью подставки
решаем с помощью подставки![]() .
.
Дифференциальные уравнения вида
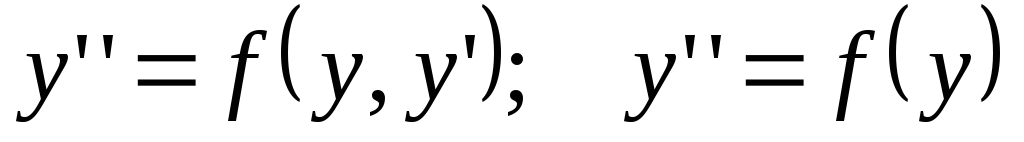 .
.
Для нахождения решения вводим новую
функцию
![]() ,
тогда
,
тогда![]() .
.
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами (ЛОДУ)
Общий вид:
![]() .
.
Ход решения:
- составляем характеристическое уравнение
вида
![]() ;
;
- решаем характеристическое равнение, используя дискриминант;
- записываем общее решение, учитывая:

ЛОДУ высших порядков решаются аналогично.
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (ЛНДУ)
Общий вид
![]() ,
где
,
где![]() - непрерывная функция при всех
рассматриваемых
- непрерывная функция при всех
рассматриваемых![]() .
.
![]() - ЛНДУ второго порядка с первой
специальной правой частью (
- ЛНДУ второго порядка с первой
специальной правой частью (![]() -
любое действительное число, включая
ноль,
-
любое действительное число, включая
ноль,![]() -
многочлен
-
многочлен![]() -ой
степени с действительными коэффициентами)
-ой
степени с действительными коэффициентами)
Его решение имеет вид:
![]() ,
где
,
где
-
![]() - общее решение соответствующего ЛОДУ
- общее решение соответствующего ЛОДУ![]() ,
,
-![]() ,
где
,
где![]() -
кратность, с которой
-
кратность, с которой![]() входит в число корней
характеристического
уравнения,
входит в число корней
характеристического
уравнения,![]() -
из условия,
-
из условия,![]() -
многочлен
-
многочлен![]() -
ой степени, взятый с буквенными
коэффициентами.
-
ой степени, взятый с буквенными
коэффициентами.
![]() - ЛНДУ второго порядка со второй
специальной правой частью (
- ЛНДУ второго порядка со второй
специальной правой частью (![]() -
любое действительное число, включая
ноль,
-
любое действительное число, включая
ноль,![]()
![]() -
многочлен
-
многочлен![]() -ой
и
-ой
и![]() -
ой степени с действительными коэффициентами)
-
ой степени с действительными коэффициентами)
Его решение имеет вид:
![]() ,
где
,
где
-
![]() - общее решение соответствующего ЛОДУ
- общее решение соответствующего ЛОДУ![]() ,
,
-![]() ,
где
,
где![]() -
кратность, с которой пара чисел
-
кратность, с которой пара чисел![]() входит в число корней характеристического
уравнения,
входит в число корней характеристического
уравнения,![]() -
из условия,
-
из условия,![]() - разные многочлены одной степени с
буквенными коэффициентами (
- разные многочлены одной степени с
буквенными коэффициентами (![]() ).
).
ЛНДУ высших порядков решают аналогично.
Теорема:
Если
![]() -
частное решение д.у.
-
частное решение д.у.![]() ,
,![]() -
частное решение д.у.
-
частное решение д.у.![]() ,
то их сумма
,
то их сумма![]() - частное решение д.у.
- частное решение д.у.![]() .
.
Метод Лагранжа (для интегрирования ЛНДУ второго и высших порядков)
Этот метод целесообразно применять при интегрировании ЛНДУ с постоянными коэффициентами, но без специальной правой части и уравнений с переменными коэффициетами.
Пусть имеем
![]() - ЛНДУ второго порядка. Найдем его решение
в виде
- ЛНДУ второго порядка. Найдем его решение
в виде![]() методом вариации.
методом вариации.
-
![]() -
решение соответствующего ЛОДУ;
-
решение соответствующего ЛОДУ;
-
![]() ;
;
- составляем СЛАУ относительно
![]() :
:
- находим по формулам Крамера решение
системы:
![]() ;
;
- итнегрируем последнее равенство и
полагаем постоянные интегрирования
равными нулю, тем самым находим
![]() ;
;
- записываем решение в виде
![]() .
.
1.4.Системы диффереренциальных уравнений.
Определение:
Система диффереренциальных уравнений
вида
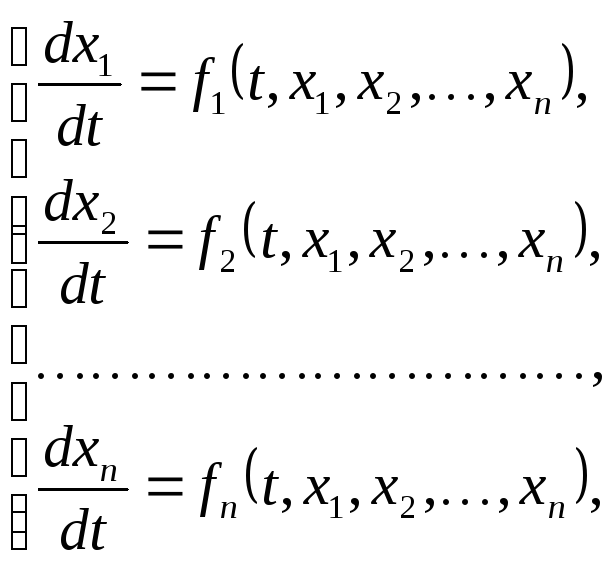
где
![]() - неизвестные функции независимой
переменной
- неизвестные функции независимой
переменной![]() ,
называется нормальной системой.
,
называется нормальной системой.
Если правые части нормальной системы
дифференциальных уравнений являются
линейными функциями относительно
![]() ,
то система дифференциальных уравнений
называется линейной.
,
то система дифференциальных уравнений
называется линейной.
1) Иногда нормальную систему дифференциальных
уравнений удается свести к одному
уравнению
![]() -
го порядка, содержащему одну неизвестную
функцию. Сведение нормальной системы
к одному уравнению может быть достигнуто
дифференцированием одного из уравнений
системы и исключением всех неизвестных,
кроме одного.
-
го порядка, содержащему одну неизвестную
функцию. Сведение нормальной системы
к одному уравнению может быть достигнуто
дифференцированием одного из уравнений
системы и исключением всех неизвестных,
кроме одного.
В некоторых случаях, комбинируя уравнения системы, после несложных преобразований удается получить легко интегрируемые уравнения, что позволяет найти решение системы.
2) Пусть дана система 3 линейных дифференциальных уравнений с 3 неизвестными функциями, коэффициенты которых постоянные:

![]()
Общее решение имеет вид:
 .
.
Здесь
![]() -
нетривиальные частные решения системы,
причем такие, что каждая тройка функций
образуют ФСР
-
нетривиальные частные решения системы,
причем такие, что каждая тройка функций
образуют ФСР![]() .
.
Ищем такие частные решения системы в
виде
![]() ,
здесь
,
здесь![]() - некоторые константы. Подставив значения
- некоторые константы. Подставив значения![]() в систему дифференциальных уравнений
в систему дифференциальных уравнений![]() ,
получим систему линейный алгебраических
уравнений относительно
,
получим систему линейный алгебраических
уравнений относительно![]() :
:

![]()
Составляем характеристическое
уравнение: .
.
Оно имеет три корня: действительных или комплексно-сопряженных.
- Если корни дейстительные и различные
![]() ,
то для каждого корня
,
то для каждого корня![]() находим
из системы
находим
из системы![]() одно из ее решений
одно из ее решений![]() вида:
вида:
![]()
Линейная комбинация полученных частных решений определит общее решение заданной системы.
- Если среди корней есть пара
комплексно-сопряженных чисел, т.е.
![]() -
действительное,
-
действительное,![]() ,
то аналогичным способом с помощью корня
,
то аналогичным способом с помощью корня![]() находим первое частное решение системы
в действительной форме. С помощью корня
находим первое частное решение системы
в действительной форме. С помощью корня![]() или
или![]() получаем
новое частное решение в комплексной
форме. Выделив в новом решении
действительные и мнимые части, составляем
из них соответственно частные решения
в действительной форме.
получаем
новое частное решение в комплексной
форме. Выделив в новом решении
действительные и мнимые части, составляем
из них соответственно частные решения
в действительной форме.
