
- •Чевын м.А.
- •1.7. Формулы Крамера:
- •Раздел II: элементы векторной алгебры.
- •Раздел III: аналитическая геометрия.
- •3.9. Плоскость в пространстве:
- •Раздел VI: уравнения и графики кривых в полярной системе координат.
- •Раздел VII: кривые, заданные параметрически.
- •Раздел VIII: нахождение пределов.
- •8.1. Определение пределов:
- •8.2. Бмф и ббф:
- •8.3. Алгоритм нахождения пределов от алгебраических функций:
- •9.2. Таблица производных:
- •9.3. Логарифмическое дифференцирование:
- •9.4. Дифференцирование функций, заданных неявно:
- •9.5. Дифференцирование функций, заданных параметрически:
- •9.6. Производные высших порядков:
- •9.7. Раскрытие неопределенностей по правилу Лопиталя:
- •9.8. Формула Тейлора:
- •9.10. Общая схема исследования функции и построения ее графика:
- •Раздел X: комплексные числа.
- •10.2. Действия над комплексными числами:
- •Раздел XI: неопределенный интеграл.
- •11.1. Определение и свойства:
- •1.2 Таблица дифференциалов и интегралов:
- •11.3 Общие методы интегрирования:
- •Раздел XII: определенный интеграл.
- •12.1. Определение и свойства:
- •12.2. Методы вычисления определенного интеграла:
- •12.3. Несобственные интегралы:
- •12.4 Применения определенного интеграла:
- •Раздел XIII: дифференциальное исчисление функций нескольких переменных.
- •13.1. Основные понятия:
- •13.2. Частные производные:
- •13.3. Дифференцирование сложных функций:
- •13.4. Дифференцирование неявных функций:
- •13.5. Касательная плоскость и нормаль к поверхности:
- •13.6. Экстремумы функции двух переменных:
- •Раздел XIV: кратные интегралы.
- •14.1. Определение и свойства двойного интеграла:
- •14.3. Применения двойного интеграла:
- •14.4. Определение и вычисление тройного интеграла:
- •14.5. Применения тройного интеграла:
- •Раздел XV: криволиненйные интегралы.
- •15.4 Криволинейный интеграл по координатам:
- •15.5 Вычисление криволинейных интегралов по координатам:
- •15.6 Применения криволинейных интегралов по координатам:
- •Раздел XVI: поверхностные интегралы.
- •16.1. Определение и свойства поверхностого интеграла по площади поверхности:
- •16.4. Определение и свойства поверхностного интеграла по координатам :
- •16.5. Вычисление поверхностных интегралов по координатам:
- •Раздел I: обыкновенные дифференциальные уравнения первого порядка.
- •1.1. Основные понятия:
- •1.3. Дифференциальные уравнения высших порядков:
- •1.4.Системы диффереренциальных уравнений.
- •Раздел II: теория поля.
- •2.2. Векторное поле и его характеристики:
- •Раздел III: ряды.
- •3.3. Знакопеременные ряды:
- •3.4. Степенные ряды:
- •3.5. Ряд Тейлора:
- •3.6. Разложение элементарных функций в ряд по степеням :
- •Раздел IV: теория функций комплексного переменного.
- •4.1. Основные понятия:
- •4.2. Основные элементарные функции:
- •4.3. Определение и свойства контурного интеграла по кривой:
- •4.4. Вычисление контурных интегралов от непрерывной функции комплексного переменного:
- •4.5. Ряды Тейлора и Лорана:
- •4.7. Вычеты:
- •Раздел V:операционное исчисление.
- •5.2. Свойства преобразований Лапласа:
- •5.3. Свертка функций:
- •5.4. Теоремы разложения:
- •5.5 Таблица оригиналов и изображений:
- •Раздел VI: основы теории вероятностей.
- •6.1. Элементы комбинаторики:
- •6.2. Основные понятия теории вероянтостей:
- •6.4. Случайные величины:
- •6.4. Числовые характеристики случайных величин:
- •3) Среднее квадратическое отклонение:
15.5 Вычисление криволинейных интегралов по координатам:
1.
![]() - в случае явного задания кривой
интегрирования;
- в случае явного задания кривой
интегрирования;
2.
 - в случае параметрического задания
кривой интегрирования;
- в случае параметрического задания
кривой интегрирования;
3.
![]() - формула Грина, где
- формула Грина, где![]() -
область, ограниченная контуром
-
область, ограниченная контуром![]() .
.
4. Если
![]() ,
то
,
то![]() ;
;
5. Если
![]() и
и![]() -
незамкнутая кривая
-
незамкнутая кривая ,
т.е. вычисление таких интегралов сводится
к вычислению определенных, однако, в
качестве линии интегрирования удобно
брать ломаную, звенья которой параллельны
осям координат.
,
т.е. вычисление таких интегралов сводится
к вычислению определенных, однако, в
качестве линии интегрирования удобно
брать ломаную, звенья которой параллельны
осям координат.
15.6 Применения криволинейных интегралов по координатам:
1.
 - нахождение функции по ее полному
дифференциалу, где
- нахождение функции по ее полному
дифференциалу, где![]() - точка из области непрерывности
- точка из области непрерывности![]() ;
;
2.
![]() - работа силы
- работа силы![]() ,
где
,
где![]() ,
по перемещению материальной точки
,
по перемещению материальной точки![]() ;
;
3.
![]() -
площадь плоской фигуры.
-
площадь плоской фигуры.
Теорема (условие независимости составного интеграла по координатам от формы кривой интегрирования):
Если функции
![]() и их частные производные первого порядка
непрерывны в некоторой области
и их частные производные первого порядка
непрерывны в некоторой области![]() ,
то для того чтобы составной интеграл
по координатам не зависел от формы
кривой интегрирования необходимо и
достаточно, чтобы в каждой точке области
,
то для того чтобы составной интеграл
по координатам не зависел от формы
кривой интегрирования необходимо и
достаточно, чтобы в каждой точке области![]() подынтегральное
выражение
подынтегральное
выражение![]()
![]() было
полным дифференциалом некоторой функции
двух переменных
было
полным дифференциалом некоторой функции
двух переменных![]() .
.
Раздел XVI: поверхностные интегралы.
16.1. Определение и свойства поверхностого интеграла по площади поверхности:
Пусть функция
![]() - непрерывна в каждой точке гладкой
поверхности
- непрерывна в каждой точке гладкой
поверхности![]() .
.
Определение:
Конечный предел интегральной суммы
функции
![]() в области
в области![]() при
условии, что
при
условии, что![]() и
и![]() называется поверхностным интегралом
по площади поверхности от функции
называется поверхностным интегралом
по площади поверхности от функции![]() по поверхности
по поверхности![]() ,
где
,
где![]() -
диаметр частичной поверхности.
-
диаметр частичной поверхности.
Т.о.
 ,
где
,
где![]() -
площадь частичной поверхности.
-
площадь частичной поверхности.
Определение:
Сторона поверхности называется
положительной (отрицательной) в
направлении оси
![]() ,
если нормаль, проведенная к этой стороне
в произвольной точке составляет с осью
,
если нормаль, проведенная к этой стороне
в произвольной точке составляет с осью![]() острый (тупой) угол.
острый (тупой) угол.
Аналогично, для
![]() .
.
Определение:
Выбор одной из двух сторон поверхностей (положительной или отрицательной) в направлении определенной оси называется ориентацией поверхности в направлении выбранной оси.
Основные свойства:
Поверхностные интегралы не завися от ориентации поверхности в направлении любой оси.
 ;
;Если всюду на

 ,
то и
,
то и ;
;Если всюду на

 ,
то и
,
то и ;
; ;
; ,
где
,
где - площадь
- площадь ,
,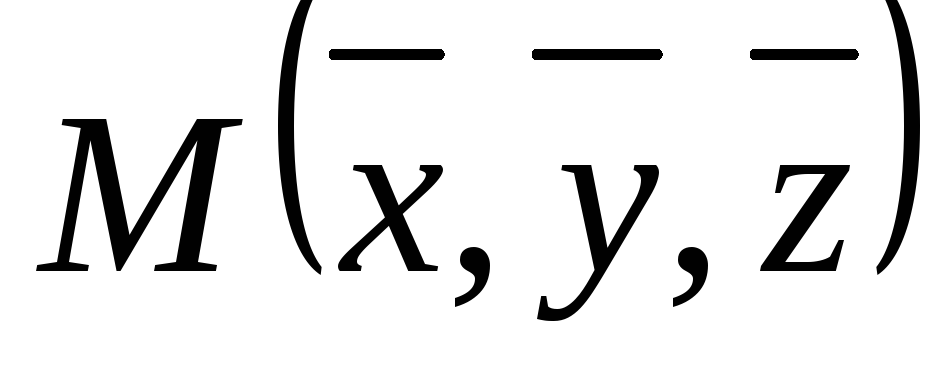 - из поверхности
- из поверхности .
.
16.2. Вычисление поверхностных интегралов по площади поверхности:
Выясняем, прямая параллельная какой оси, пересекает эту поверхность не более чем в одной точке;
Тогда уравнение
 разрешаем относительно этой переменной,
проецируем
разрешаем относительно этой переменной,
проецируем на соответствующую двумерную плоскость.
на соответствующую двумерную плоскость.
Т.е., если такая прямая параллельна оси
![]() :
:
- уравнение
![]() :
:![]() ;
;
- проецируем
![]() на
на![]() и
и![]() .
.
3. Переходим к двойному интегралу:
![]() .
.
16.3. Применения поверхностных интегралов по площади поверхности:
 - площадь поверхности
- площадь поверхности ;
; - масса гладкой неоднородной поверхности
- масса гладкой неоднородной поверхности с плотностью
с плотностью ;
; ;
; ;
; -
статические моменты относительно
координатных плоскостей;
-
статические моменты относительно
координатных плоскостей; ;
; ;
; ; - координаты центра масс поверхности;
; - координаты центра масс поверхности;
 - моменты инерции поверхности относительно
координатных осей.
- моменты инерции поверхности относительно
координатных осей.
