9.8. Формула Тейлора:
,
где
,
-
некоторая точка окрестности
.
Формула Тейлора позволяет приближенно представлять функции в виде многочленов любой требуемой степени и определяет погрешность такого представления.
9.10. Общая схема исследования функции и построения ее графика:
Устанавливаем область определения
,
точки разрыва, интервалы непрерывности.Исследуем функцию на четность, нечетность, периодичность.
Находим ВАС:
,
где
-
такое значение аргумента при котором
функция
становится
бесконечно большой
Находим НАС:
,
где
(если хотя бы один из пределов не
существует или равен бесконечности, то
график не имеет НАС).
Определяем интервалы монотонности и экстремумы с помощью первой производной.
Находим интервалы вогнутости, выпуклости, точки перегиба с помощью второй производной.
Определяем точки пересечения графика с осями координат (если с осью
,
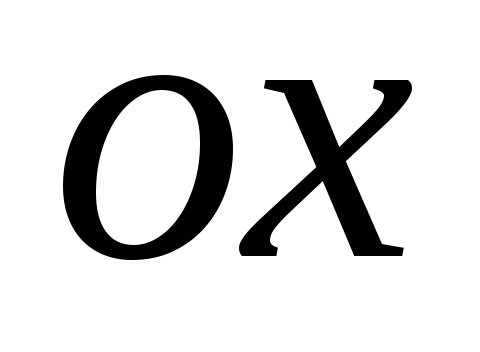то решаем уравнение
,
если с осью
,
то находим
).Если график не имеет НАС, то исследуем поведение
при
.
8) Строит график функции.
Раздел X: комплексные числа.
Основные понятия:
Определение:
Комплексным числом
называется
упорядоченная пара действительных
чисел
представленная выражением
,
здесь
- называют мнимой единицей.
и
называются комплексно-сопряженными.
Комплексное число можно изобразить
точкой плоскости
:
с координатами
или радиус вектором этой точки.
Формы записи комплексного числа:
- алгебраическая
- тригонометрическая
- показательная.
Модуль комплексного числа:
.
Основное значение аргумента комплексного числа:
- аргумент комплексного числа.
Если комплексное число лежит на одной из координатных осей, то ее главный аргумент находят непосредственно.
10.2. Действия над комплексными числами:
В алгебраической форме:
Если
,
то
1.
.
2.
.
3.
,
учитывая
.
.
4.
,
но чаще
.
В тригонометрической и показательной формах:
Если
,
то
1.
.
В частности:
2.
.
3.
.
Раздел XI: неопределенный интеграл.
11.1. Определение и свойства:
Определение:
Функция
называется первообразной функции
в промежутке
,
если в каждой точке этого промежутка
выполняется равенства:
или
.
Определение:
Совокупность всех первообразных функции
в
называется неопределенным интегралом
от этой функции в данном промежутке.
Обозначение:
.
Основные свойства неопределенного интеграла:
1.
2.
3.
4.
5.
6. Если
то
,
где
- любая непрерывно - дифференцируемая
функция.
1.2 Таблица дифференциалов и интегралов:
|
Таблица интегралов |
Таблица дифференциалов |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
12.
|
12.
|
|
13.
|
13.
|
|
14.
|
14.
|
|
15.
|
15.
|
|
16.
|
|
|
17.
|
|
|
18.
|
|
|
19.
|
|
|
20.
|
|
|
21.
|
|
|
22.
23.
|
|
