5. Метод Зейделя
При решении системы линейных уравнений вычислительные формулы имеют вид:
(3.27)
где
.
Из (3.27) видно, что в методе простой итерации для получения нового значения вектора решений на i+1-ом шаге используются значения переменных, полученные на предыдущем шаге.
Основная
идея метода Зейделя состоит в том, что
на каждом шаге итерационного процесса
при вычислении значения переменной
учитываются уже найденные значения
:
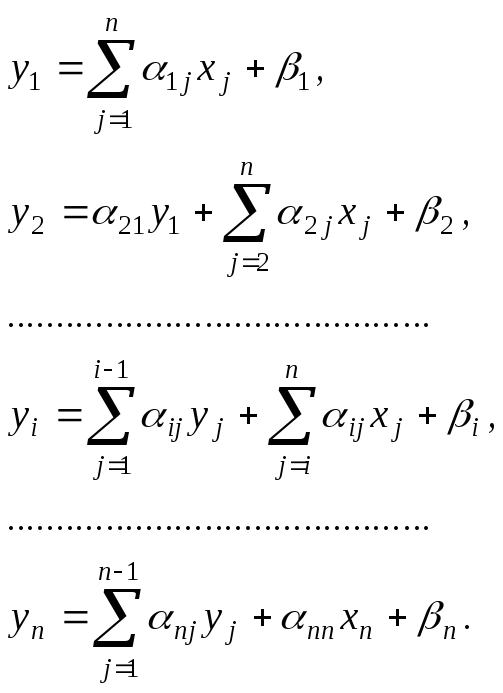(3.28)
Достаточные условия сходимости итерационного процесса (3.23)(3.25) также являются достаточным условиями сходимости метода Зейделя.
Существует возможность автоматического преобразования исходной системы к виду, обеспечивающему сходимость итерационного процесса метода Зейделя. Для этого умножим левую и правую части системы (3.2) на транспонированную матрицу системы AT, получим равносильную систему
,
(3.29)
где
,
.
Система (3.29) называется нормальной системой уравнений. Нормальные системы уравнений обладают рядом свойств, среди которыхможно выделить следующие:
1)
матрица C
коэффициентов при неизвестных нормальной
системы является симметрической (т.е.
,
);
2)
все элементы, стоящие на главной диагонали
матрицы C
положительны (т.е.
,
).
Последнее свойство дает возможность «автоматически» приводить нормальную систему (3.29) к виду, пригодному для итерационного процесса Зейделя:
(3.30)
где
,
(3.31)
и
.
(3.32)
Целесообразность приведения системы к нормальному виду и использования метода Зейделя вытекает из следующей теоремы:
Теорема 3.2. Итерационный процесс метода Зейделя для приведенной системы (3.30), эквивалентной нормальной системе (3.29), всегда сходится к единственному решению этой системы при любом выборе начального приближения [2].
Таким образом решение произвольной системы линейных уравнений вида (3.1) методом Зейделя реализуется в соответствие со следующим алгоритмом:
1. Ввод матрицы А коэффициентов исходной системы и вектор-столбца свободных членов.
2. Приведение системы к нормальной умножением обеих частей системы на транспонированную матрицу АT.
3. Приведение нормальной системы к виду, пригодному для итерационного процесса Зейделя (3.30), (3.31).
4. Задание требуемой точности решения.
5. Циклическое выполнение итерационного процесса до достижения требуемой точности.
Для реализации метода Зейделя в пакете MATLAB необходимо:
1. Создать файл Zeidel.m, содержащий описание функции, выполняющей последовательно: а) приведение системы к нормальному виду; б) приведение нормальной системы к виду, пригодному для итерационного процесса Зейделя; в) реализацию итерационного процесса Зейделя.
% листинг файла Zeidel.m
function [z1,z2]=Zeidel(A,b,eps)
N=size(A,1);
% приведение системы к нормальному виду
C=A'*A;
D=A'*b;
% приведение системы к виду пригодному для итерационного процесса
% Зейделя
for i=1:N
D1(i)=D(i)/C(i,i);
end;
D1=D1'; % транспонирование матрицы
d1=D1;
for i=1:N
for j=1:N
if i==j
C1(i,j)=0;
else
C1(i,j)=-C(i,j)/C(i,i);
end;
end;
end;
% решение системы линейных уравнений методом Зейделя
R1=d1;
while Flag==0
for i=1:N
v=C1(i,1:N); % выделение i-oй строки матрицы
a=dot(v',d1); % вычисление скалярного произведения
d1(i)=a+D1(i);
end;
R2=d1;
s=max(abs(R2-R1));
if s<eps
z1=d1;
z2=s;
return
end;
R1=R2;
end;
2. Задать матрицу коэффициентов при неизвестных исходной системы линейных уравнений и столбец свободных членов
>> A=[1,2,3,4,5;10,9,8,7,6;5,9,11,12,13;20,1,3,17,14;12,10,4,16,15]
>> b=[10,20,30,40,50];
3. Вычислить решение системы линейных уравнений, используя функцию Zeidel( )
>> Zeidel1(A,b,10^-6)
ans =
0.0972
1.4325
-1.3533
1.6564
0.8947
4. Проверить полученное решение
>> A*ans
ans =
10.0013
20.0003
29.9995
39.9999
50.0000