7.5. Аппроксимация функцией произвольного вида
Для решения задачи обобщенной нелинейной регрессии в пакете MATLAB имеется функция lsqnonlin( ), возвращающая решение задачи нахождения точки минимума функции f(x)
,
где в общем случае f(x) вектор-функция, x вектор-столбец искомых переменных, L некоторая константа.
Синтаксис функции lsqnonlin( ):
x = lsqnonlin(fun,x0)
x = lsqnonlin(fun,x0,lb,ub)
x = lsqnonlin(fun,x0,lb,ub,options)
x = lsqnonlin(fun,x0,eb,ub,options,P1,P2, ... )
[x,resnorm] = lsqnonlin(...)
[x,resnorm,residual] = lsqnonlin(...)
[x,resnorm,residual,exitflag] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output,lambda] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output,lambda,jacobian] =
lsqnonlin(...)
аналогичен
синтаксису функции fsolve( ),
подробно обсуждавшемся нами в лекции
№ 4. Поэтому далее мы ограничимся только
примером, демонстрирующим использование
данной функции для нахождения параметров
функции
.
Для решения данной задачи в пакете MATLAB необходимо выполнить следующую последовательность действий:
1. Создать файл F77.m, содержащий описание функции, возвращающей значения вектор-функции f(x)
% листинг файла F77.m
function z=F77(Coeff,vx,vy)
k=1:length(vx);
z=vy-exp(Coeff(1)+Coeff(2)*vx+Coeff(3)*vx.^2);
2. Выполнить следующую последовательность команд
% задание исходных данных
>> vx=[0.3;0.4;1;1.4;2;4]
vx =
0.3000
0.4000
1.0000
1.4000
2.0000
4.0000
>> vy=[9.4;11.2;5;3;6;0.2]
vy =
9.4000
11.2000
5.0000
3.0000
6.0000
0.2000
>> z=[1 0 -1] % начальное приближения
z =
1 0 -1
% вычисление коэффициентов аппроксимирующей функции
>> Coeff = lsqnonlin('F77',z',[],[],[],vx,vy)
Optimization terminated successfully:
Relative function value changing by less than OPTIONS.TolFun
Coeff =
2.5696
-0.8037
0.0462
>> F=inline('exp(a+b*x+c*x.^2)','x','a','b','c'); % задание
% аппроксимирующей функции
>> X=vx(1):0.01:vx(length(vx)); % координаты абсцисс, в которых
% будут вычисляться значения
% аппроксимирующей функции
>> Y=feval(F,X,Coeff(1),Coeff(2),Coeff(3)); % вычисление значений
% аппроксимирующей функции
>> i=1:length(vx);
>> j=1:length(X);
>> plot(vx(i),vy(i),'o',X(j),Y(j)) % (рис. 7.4)
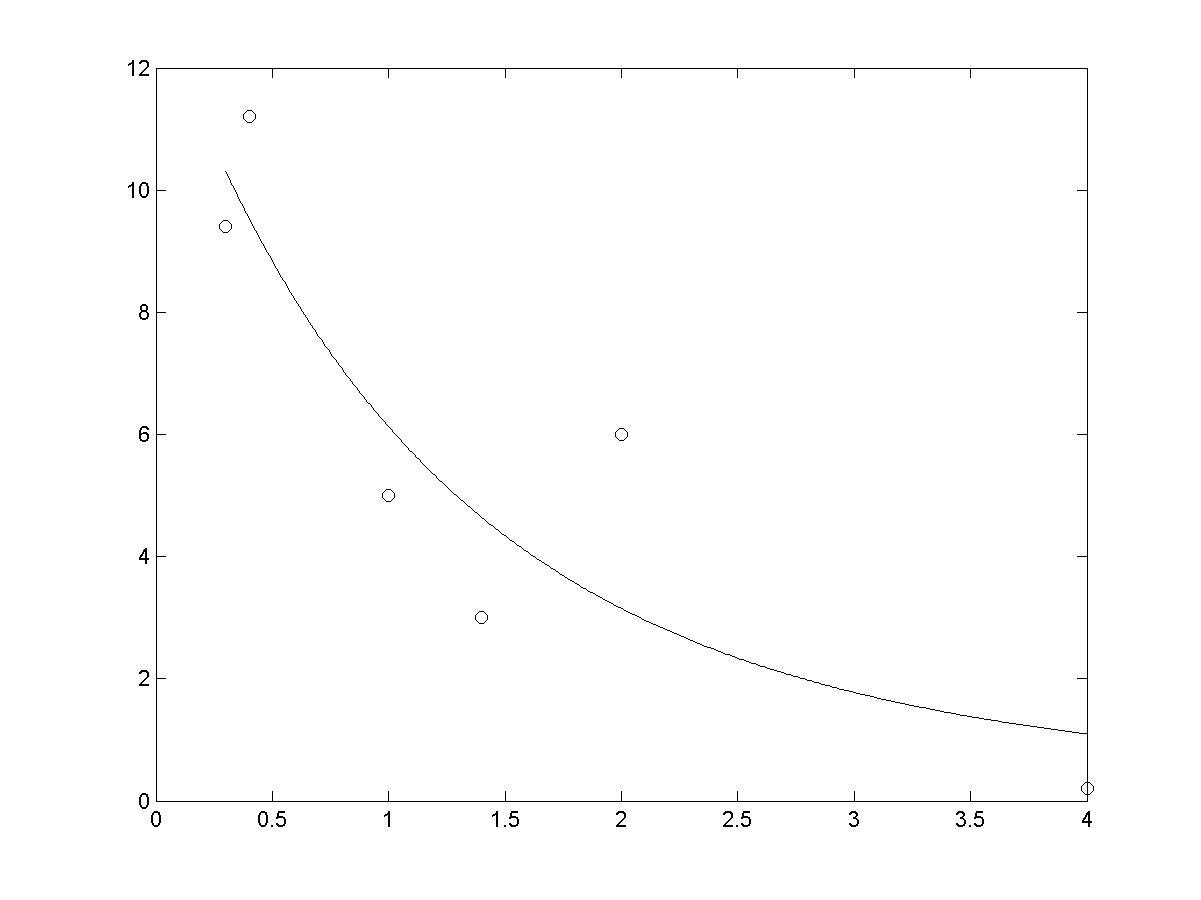
Рис. 7.4
Лекция № 8. Преобразование Фурье
План
8.1. Разложение периодических функций в ряд Фурье
8.2. Эффект Гиббса
8.3. Спектральный анализ дискретных функций конечной длительности
8.4. Быстрое преобразование Фурье
8.1. Разложение периодических функций в ряд Фурье
По определению периодической функцией называют функцию, отвечающую условию:
,
(8.1)
где
T
– период функции,
Для нахождения спектрального разложения функции s(t) введем в рассмотрение следующие наборы функций:
(8.2)
Любая
из функций (8.2), которую для краткости
обозначим
,
удовлетворяет условию периодичности
(8.1).
Рассмотрим три следующие интеграла:
,
,
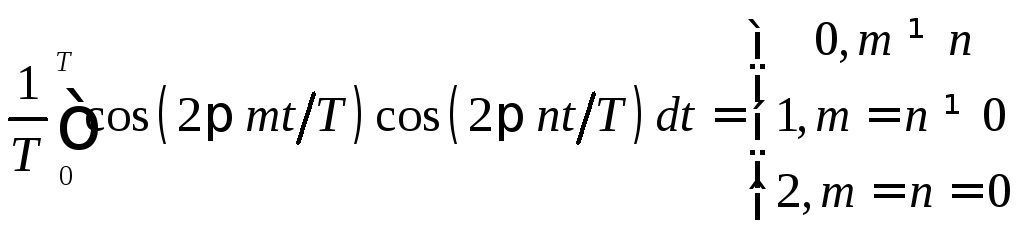(8.3)
.
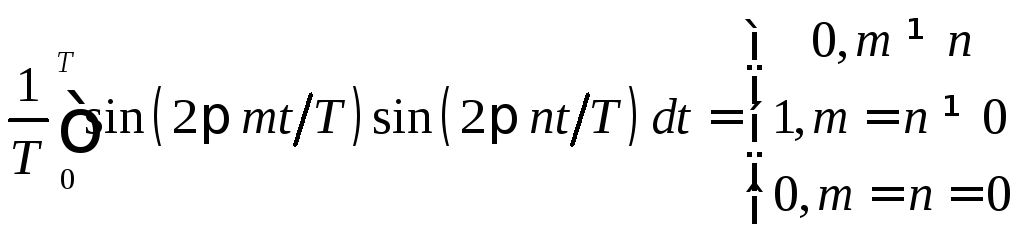Функции, удовлетворяющие условию (8.3), называются ортогональными, а систему функций (8.2) называют ортонормированным базисом, образованным гармоническими функциями с кратными частотами. Условие ортогональности можно записать в компактной форме, используя символ Кронекера:
,
(8.4)
где
.
Разложим
произвольную периодическую функцию
в ряд
.
(8.5)
Представление
(8.5) называется обобщенным рядом Фурье
функции
в выбранном базисе.
Коэффициенты
данного ряда находятся умножением (8.5)
на базисную функцию
и интегрированием по периоду функции
:
.
(8.6)
Откуда, используя свойство ортонормированности (8.4), найдем
.
(8.7)
Подставляя в (8.7) набор функций (8.2), найдем значения коэффициентов ряда:
,
(8.8а)
,
(8.8b)
.
(8.8c)
Введя
основную частоту
последовательности, образующей
периодическую функцию
,
запишем ряд Фурье для периодического
сигнала
.
(8.9)
Анализ
(8.9) показывает, что функция
содержит независящую от времени
постоянную составляющую и бесконечный
набор гармонических колебаний, так
называемых, гармоник с частотами
(
),
кратными основной частоте последовательности.
Можно показать, что имеет место равенство
(8.10)
Если записать коэффициенты ряда Фурье в виде
,
где
,
то получим эквивалентную форму ряда Фурье:
.
(8.11)
Спектральное
разложение периодической функции
можно выполнить используя систему
базисных функций в виде экспонент с
мнимыми показателями:
,
(8.12)
которые, как легко убедиться, вычислив интеграл
,
являются ортогональными.
Ряд Фурье в данном случае принимает вид
(8.13)
с коэффициентами
.
(8.14)
На практике принято использовать и другую форму записи ряда Фурье:
,
(8.15)
где
.
(8.16)
Выражения (8.13) –
(8.16) представляют собой ряд Фурье в
комплексной форме. Спектр функции
в соответствие с формулами (8.15), (8.16)
содержит компоненты на отрицательной
полуоси частот, причем
,
поэтому слагаемые с положительными и
отрицательными частотами объединяются
в пары, например:
.
Таким образом, отрицательная частота является не физическим, а математическим понятием, вытекающим из способа представления комплексных чисел.
Отметим, что в технической литературе, посвященной анализу сигналов, задачу вычисления коэффициентов разложения функции в ряд Фурье называют задачей анализа, а задачу восстановления функции по известным коэффициентам ряда Фурье задачей синтеза.