5.2. Интерполяционный полином Лагранжа

Для функции, заданной табл. 5.1, построим интерполяционный многочлен , степень которого не вышеn и выполнены условия (5.1).

Будем искать в виде

, (5.5)

где  многочлен степени n, причем

. (5.6)

Очевидно, что требование (5.6) с учетом (5.5) обеспечивают выполнение условий (5.1).

Многочлены составим следующим способом:

, (5.7)

где  постоянный коэффициент, значение которого находится из первой части условия (5.6):

. (5.8)

Подставив в (5.7) и далее в (5.5), окончательно получим:

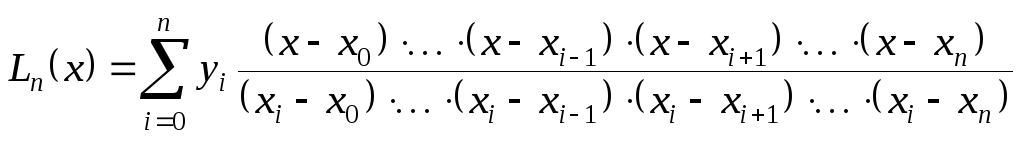. (5.9)

Формула (5.9) окончательно решает поставленную задачу.

Решение задачи интерполяции в пакете MatLAB с помощью полинома Лагранжа находится выполнением следующей последовательности команд:

1. Задать табличные значения интерполируемой функции

>> N=8;

>> i=1:N;

>> x(i)=2*pi/(N-1)*(i-1);

>> y=sin(x);

2. Создать файл Lagrange.m, содержащий описание функции возвращающей значение многочлена .

% листинг файла Lagrange.m

function z=Lagrange(x,i,X,Y)

% x  абцисса точки интерполяции

% i  номер полинома Лагранжа

% X  вектор, содержащий абсциссы узлов интерполяции

% Y  вектор, содержащий ординаты точек интерполяции

N=length(X);

L=1;

for j=1:N

if not(j==i)

L=L*(x-X(j))/(X(i)-X(j));

end;

end;

z=L*Y(i);

3. Создать файл Pol_Lagr.m, содержащий описание функции, возвращающей значения полинома Лагранжа

% листинг файла Lagr.m

function z=Pol_Lagr(x,X,Y)

% x  абцисса точки интерполяции

% i  номер полинома Лагранжа

% X  вектор, содержащий абсциссы узлов интерполяции

% Y  вектор, содержащий ординаты точек интерполяции

N=length(X);

s=0;

for i=1:N

s=s+Lagrange(x,i,X,Y);

end;

z=s;

5. Задать число промежуточных точек, вычислить их координаты и точные значения интерполируемой функции

>> M=1000;

>> j=1:M;

>> X(j)=2*pi/(M-1)*(j-1);

>> Y=sin(X);

6. Вычислить значения полинома Лагранжа в промежуточных точках

>> for j=1:M

Y2(j)=Pol_Lagr(X(j),x,y);

end;

7. Построить разность между точными и интерполированными значениями функции (рис. 5.3)

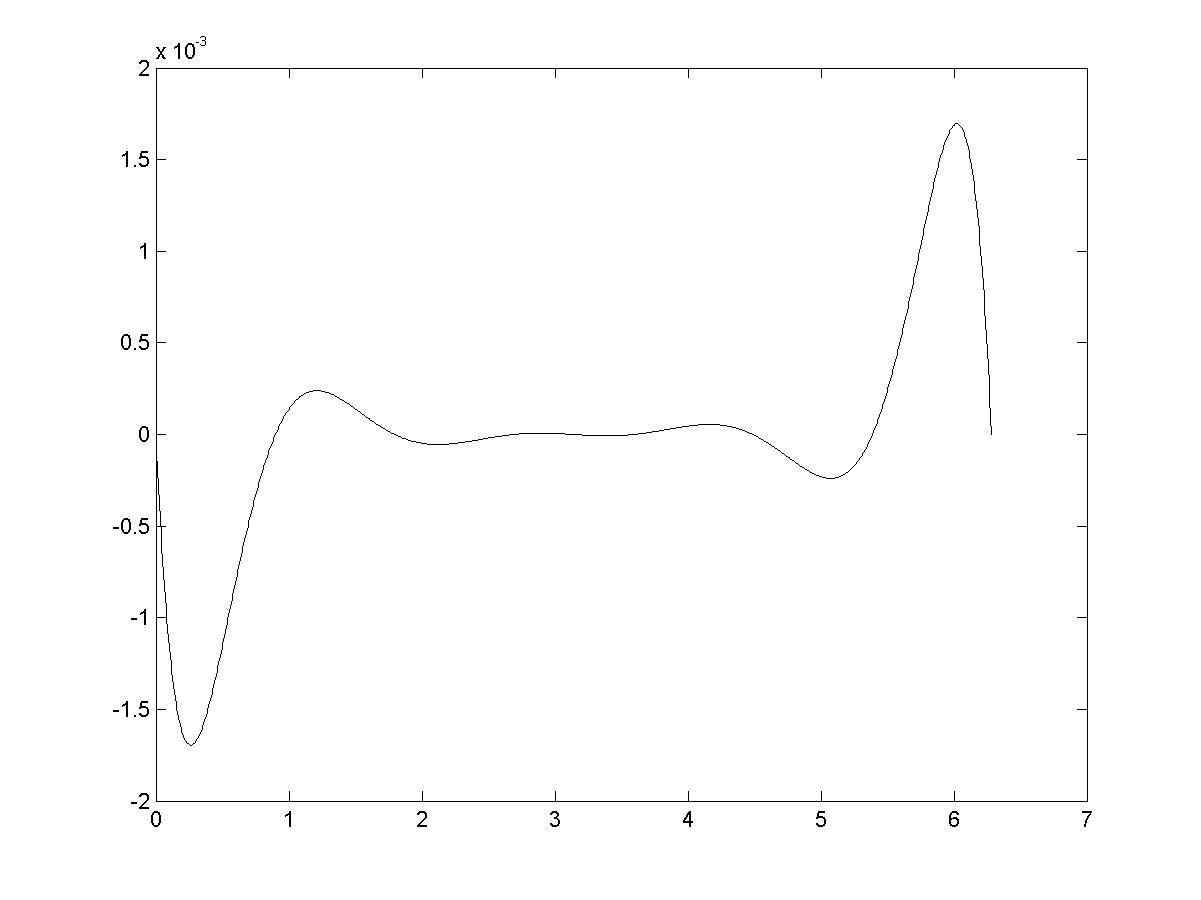
Рис. 5.3. Погрешность аппроксимации функции sin(x) полиномом Лагранжа

5.3. Интерполяционный полином Ньютона для равноотстоящих узлов

Интерполяционные формулы Ньютона строятся для функций, заданных таблицами с равноотстоящими значениями аргумента h:

. (5.10)

5.3.1. Конечные разности

Для функции, заданной табл. 5.1 с постоянным шагом (5.10), определим разности между значениями функции в соседних узлах интерполяции:

, (5.11)

называемые конечными разностями первого порядка.

Из конечных разностей первого порядка можно образовать конечные разности второго порядка:

. (5.12)

Аналогично получают выражение для конечных разностей третьего порядка:

. (5.13)

Методом математической индукции можно доказать, что

. (5.14)