
- •Содержание
- •Лекция № 1. Теория погрешностей План
- •1.1. Источники и классификация погрешностей
- •1.2. Абсолютная и относительная погрешности. Формы записи данных
- •1.3. Вычислительная погрешность
- •2.1. Общие сведения и определения
- •2.2. Отделение корней
- •2.3. Метод половинного деления
- •2.4. Метод простой итерации
- •2.5. Преобразование уравнения к итерационному виду
- •2 0.777373 -3.32063 Search
- •Лекция № 3. Методы решения систем линейных алгебраических уравнений План
- •3.1. Общие сведения и основные определения
- •3.2. Метод Гаусса и его реализация в пакете matlab
- •3.3. Вычисление определителей
- •3.4. Решение систем линейных уравнений методом простой итерации
- •5. Метод Зейделя
- •3.6. Решение систем линейных уравнений средствами пакета matlab
- •Выражения
- •Лекция № 4. Методы решения систем нелинейных уравнений
- •4.2. Метод Ньютона решения систем нелинейных уравнений
- •Последовательные приближения корней
- •4.3. Решение нелинейных систем методами спуска
- •4.4. Решение систем нелинейных уравнений средствами пакета matlab
- •Iteration Func-count f(X) step optimality cg-iterations
- •Iteration Func-count f(X) step optimality cg-iterations
- •Лекция № 5. Интерполирование функций План
- •5.1. Постановка задачи
- •Решение задачи находится отысканием некоторой приближающей функции f(X), близкой в некотором смысле к функции f(X), для которой известно аналитическое выражение/
- •5.2. Интерполяционный полином Лагранжа
- •5.3. Интерполяционный полином Ньютона для равноотстоящих узлов
- •5.3.1. Конечные разности
- •5.3.2. Первая интерполяционная формула Ньютона
- •5.3.3. Вторая интерполяционная формула Ньютона
- •5.4. Погрешность интерполяции
- •5.5. Сплайн-интерполяция
- •5.6. Решение задачи одномерной интерполяции средствами пакете matlab
- •Лекция № 6. Численное дифференцирование
- •6.2. Особенности задачи численного дифференцирования функций, заданных таблично
- •6.3. Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)
- •6.4. Погрешность численного интегрирования
- •6.5. Вычисление интегралов методом Монте-Карло
- •Лекция № 7. Методы обработки экспериментальных данных План
- •7.1. Метод наименьших квадратов
- •Сумма квадратов отклонений
- •7.2. Нахождение приближающей функции в виде линейной функции и квадратичного трехчлена
- •7.5. Аппроксимация функцией произвольного вида
- •Лекция № 8. Преобразование Фурье
- •8.2. Эффект Гиббса
- •8.3. Спектральный анализ дискретных функций конечной длительности
- •8.4. Быстрое преобразование Фурье
- •Лекция № 9. Численные методы решения обыкновенных дифференциальных уравнений План
- •9.1. Основные сведения и определения
- •9.2. Метод Пикара
- •9.3. Метод Эйлера
- •9.4. Метод Рунге-Кутта
- •9.5. Средства пакета matlab для решения обыкновенных дифференциальных уравнений
9.2. Метод Пикара
Метод Пикара позволяет получить приближенное решение дифференциального уравнения (9.2) в виде функции, заданной аналитически.
Пусть
в условиях теоремы существования
требуется найти решения (9.2) с начальным
условием
![]() .
Запишем уравнение (9.1) в следующем
эквивалентном виде
.
Запишем уравнение (9.1) в следующем
эквивалентном виде
![]() .
(9.14)
.
(9.14)
Проинтегрируем
обе части (9.14) от
![]() доx:
доx:
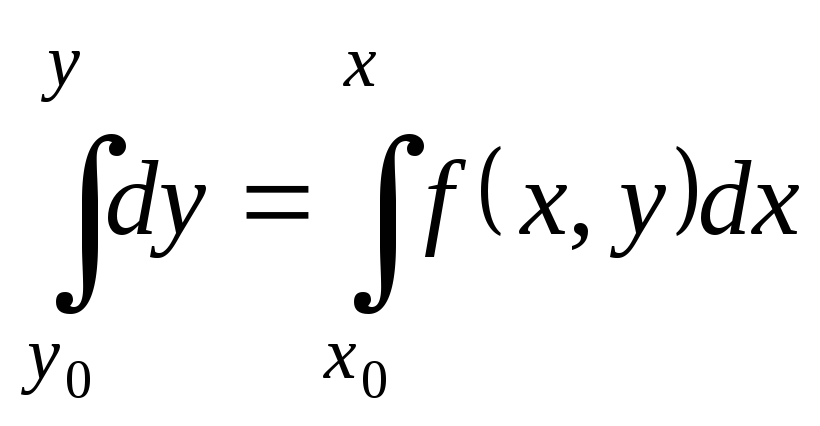 .
(9.15)
.
(9.15)
Вычислив интеграл в правой части, получим
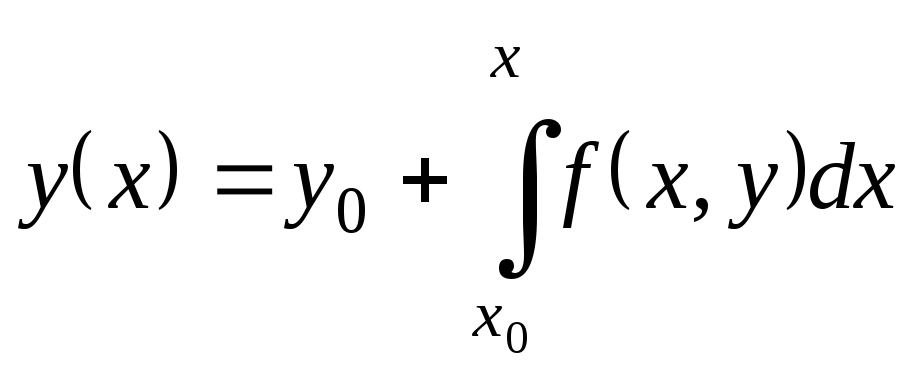 .
(9.16)
.
(9.16)
Очевидно,
что решение интегрального уравнения
(9.16) будет удовлетворять ДУ (9.2) и начальному
условию
![]() .
Действительно, при
.
Действительно, при![]() получим:
получим:
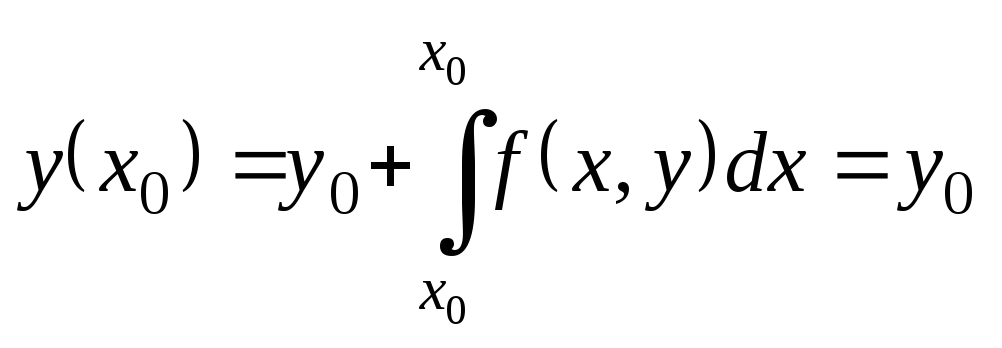 .
.
Интегральное
уравнение (9.16) позволяет использовать
метод последовательных приближений.
Положим
![]() и получим из (9.16) первое приближение:
и получим из (9.16) первое приближение:
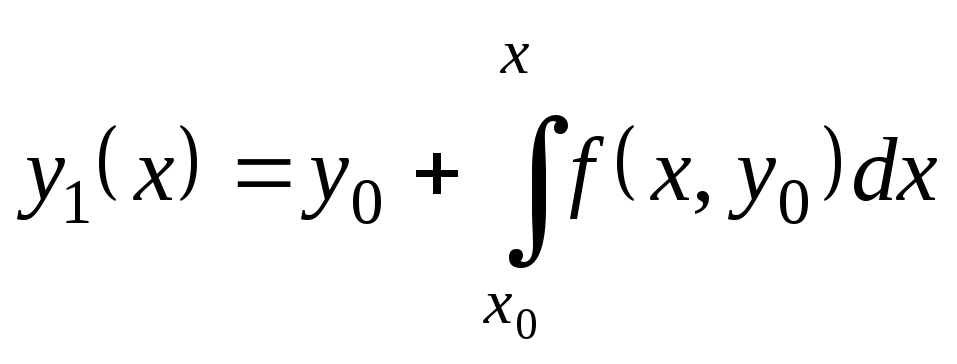 .
(9.17)
.
(9.17)
Интеграл,
стоящий в правой части (9.17) содержит
только переменную x,
после нахождения этого интеграла будет
получено аналитическое выражение
приближения
![]() как функции переменнойx.
Заменим теперь в уравнении (9.16) y
найденным значением
как функции переменнойx.
Заменим теперь в уравнении (9.16) y
найденным значением
![]() и получим второе приближение:
и получим второе приближение:
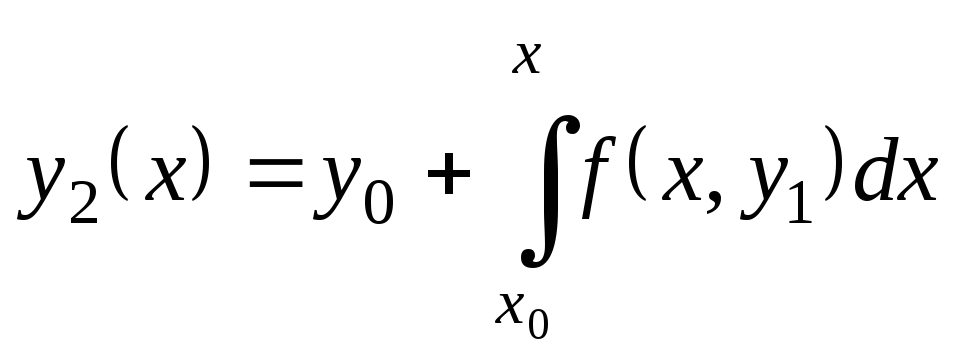 (9.18)
(9.18)
и т.д.
В общем случае итерационная формула имеет вид:
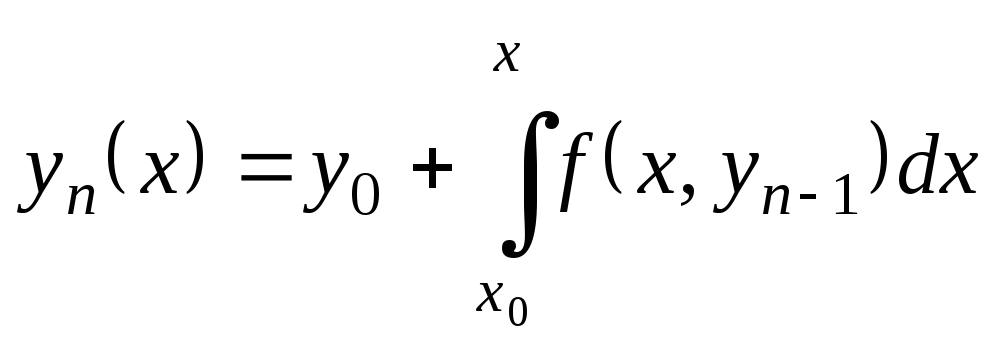
![]() (9.19)
(9.19)
Последовательное применение формулы (9.19) дает последовательность функций
![]() (9.20)
(9.20)
Так
как функция f
непрерывна в области G,
то она ограничена в некоторой области
![]() ,
содержащей точку
,
содержащей точку![]() ,
т.е.
,
т.е.
![]() .
(9.21)
.
(9.21)
Применяя
к уравнению (9.19) принцип сжимающих
отображений можно показать, что
последовательность (9.20) сходится по
метрике
![]() в пространстве непрерывных функций,
определенных на сегменте
в пространстве непрерывных функций,
определенных на сегменте
![]() ,
таких, что
,
таких, что![]() .
Предел последовательности является
решением интегрального уравнения
(9.16), а, следовательно, и дифференциального
уравнения (9.2) с начальными условиями
.
Предел последовательности является
решением интегрального уравнения
(9.16), а, следовательно, и дифференциального
уравнения (9.2) с начальными условиями![]() .
Это означает, чтоk-й
член последовательности (9.20) является
приближением к точному решению уравнения
(9.2) с определенной степенью точности.
.
Это означает, чтоk-й
член последовательности (9.20) является
приближением к точному решению уравнения
(9.2) с определенной степенью точности.
Оценка погрешности k-го приближения дается формулой:
![]() ,
(9.22)
,
(9.22)
где
M
константа Липшица (9.7), N
верхняя грань модуля функции f
из неравенства (9.21), а величина d
для определения окрестности
![]() вычисляется по формуле
вычисляется по формуле
![]() .
(9.23)
.
(9.23)
9.3. Метод Эйлера
В основе метода Эйлера лежит идея графического построения решения ДУ (рис. 9.1).
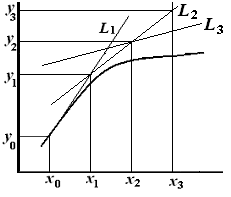
Рис. 9.1
Пусть
дано уравнение (9.2) с начальным условием
![]() .
Выбрав достаточно малый шагh,
построим, начиная с точки
.
Выбрав достаточно малый шагh,
построим, начиная с точки
![]() ,
систему равноотстоящих точек
,
систему равноотстоящих точек![]()
![]() .
Вместо искомой интегральной кривой на
отрезке
.
Вместо искомой интегральной кривой на
отрезке![]() рассмотрим отрезок касательной к ней
в точке
рассмотрим отрезок касательной к ней
в точке![]() ,
уравнение которой
,
уравнение которой![]() .
.
При
![]() из уравнения касательной получаем
из уравнения касательной получаем![]() .
Следовательно, приращение функции на
первом шаге равно
.
Следовательно, приращение функции на
первом шаге равно![]() .
.
Проведя
аналогично касательную к интегральной
кривой в точке в точке
![]() ,
получим:
,
получим:
![]() ,
,
что
при
![]() дает
дает![]() ,
т.е.
,
т.е.![]() получается из
получается из![]() добавлением приращения
добавлением приращения![]() .
.
Таким образом, вычисление таблицы значений функции, являющейся решением ДУ (2.8), состоит в последовательном применении пары формул:
![]() ,
(9.24)
,
(9.24)
![]() .
(9.25)
.
(9.25)
Метод Эйлера, как, видно из рисунка, имеет погрешность. Определим локальную погрешность, присутствующую на каждом шаге, которая определяется разностью между точным значением функции и соответствующим значением касательной. Для первого шага:
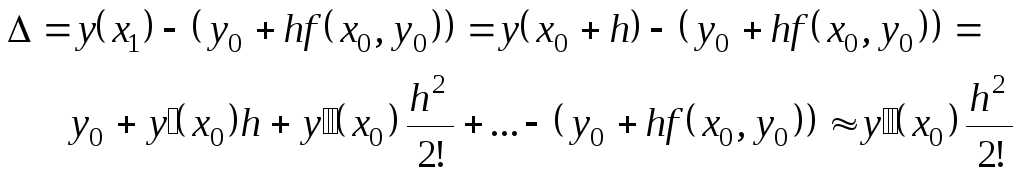 (9.26)
(9.26)
Из
(9.26) видно, что локальная погрешность
пропорциональна
![]() .
Суммарная погрешность
.
Суммарная погрешность![]() послеN
шагов пропорциональна
послеN
шагов пропорциональна
![]() ,
поскольку
,
поскольку![]() ,
то
,
то![]() ,
т.е. метод Эйлера
метод первого порядка точности по h.
,
т.е. метод Эйлера
метод первого порядка точности по h.
Известны
различные уточнения метода Эйлера.
Модификации данных методов направлены
на уточнение направления перехода из
точки
![]() в точку
в точку![]() Например, в методе ЭйлераКоши
используют следующий порядок вычислений:
Например, в методе ЭйлераКоши
используют следующий порядок вычислений:
![]() ,
,
![]() .
(9.27)
.
(9.27)
Геометрически
это означает, что определяется направление
интегральной кривой в исходной точке
![]() и во вспомогательной точке
и во вспомогательной точке![]() ,
а в качестве окончательного берется
среднее значение этих направлений.
,
а в качестве окончательного берется
среднее значение этих направлений.
Пример 9.1. Найти решение задачи Коши дифференциального уравнения
![]() ,
,
![]() ,
,
методами Эйлера и методом Эйлера-Коши.
1. Нахождение численного решения ДУ методом Эйлера.
Для нахождения решения данного ДУ необходимо создать файл Euler.m, содержащий описание функции, возвращающей решение дифференциального уравнения методом Эйлера.
% листинг файла euler_g9.m
function [X,Y]=Euler_g9(y0,x0,x1,N)
dx=(x1-x0)/N;
x(1)=x0;
y(1)=y0;
for i=1:N
x(i+1)=x(1)+dx*i;
y(i+1)=y(i)+dx*F9(x(i));
end;
X=x;
Y=y;
function z=F9(x)
z=x.^2;
Далее необходимо выполнить следующую последовательность команд:
>> x0=0; % левая граница отрезка интегрирования
>> x1=5; % правая граница отрезка интегрирования
>> y0=1.3; % начальное условие
>> N=50; % число узлов разбиения отрезка интегрирования
>> [X Y]=Euler_g9(y0,x0,x1,N); % нахождение численного решения
% задачи Коши
>> i=1:length(X);
>> Z(i)=y0+1/3*X(i).^3; % вычисление значений точного решения
>> plot(X,Z,X,Y,':') % визуализация точного и численного решений
% (рис. 9.2)
>> plot(X,abs(Z-Y)) % визуализация разности между численным и
% точным решениями ДУ (рис. 9.3)
2. Нахождение численного решения ДУ методом Эйлера-Коши.
Для нахождения решения данного ДУ необходимо создать файл EulerKoshi, содержащий описание функции, возвращающей решение дифференциального уравнения методом Эйлера-Коши.
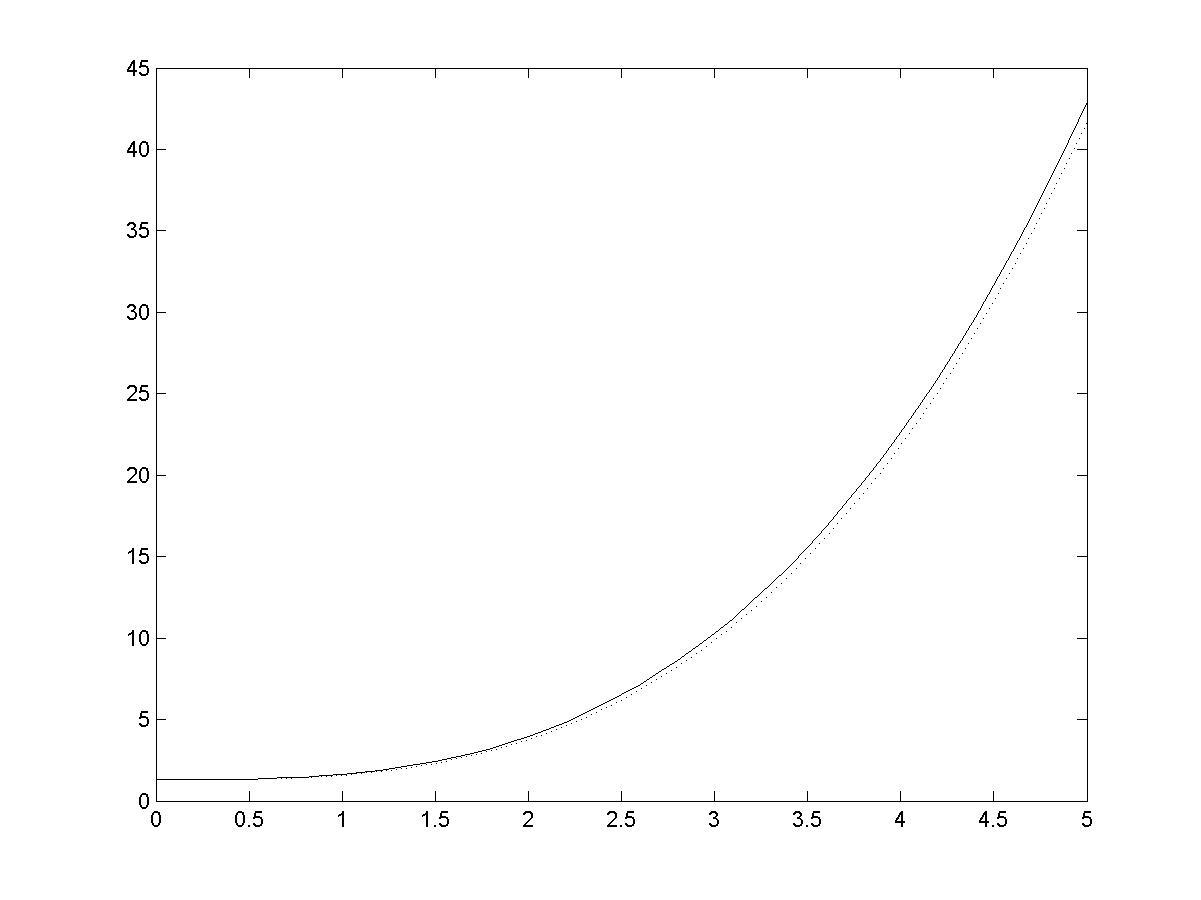
Рис. 9.2
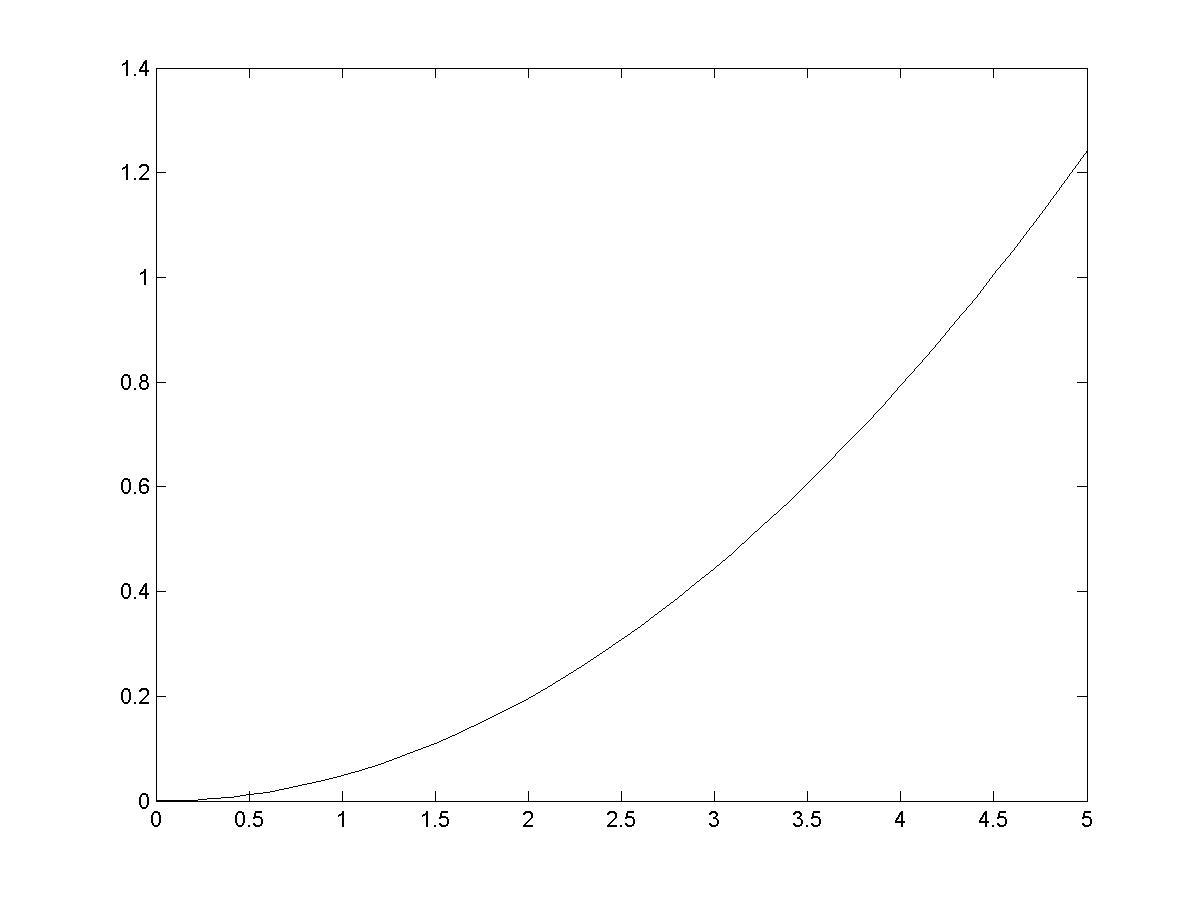
Рис. 9.3
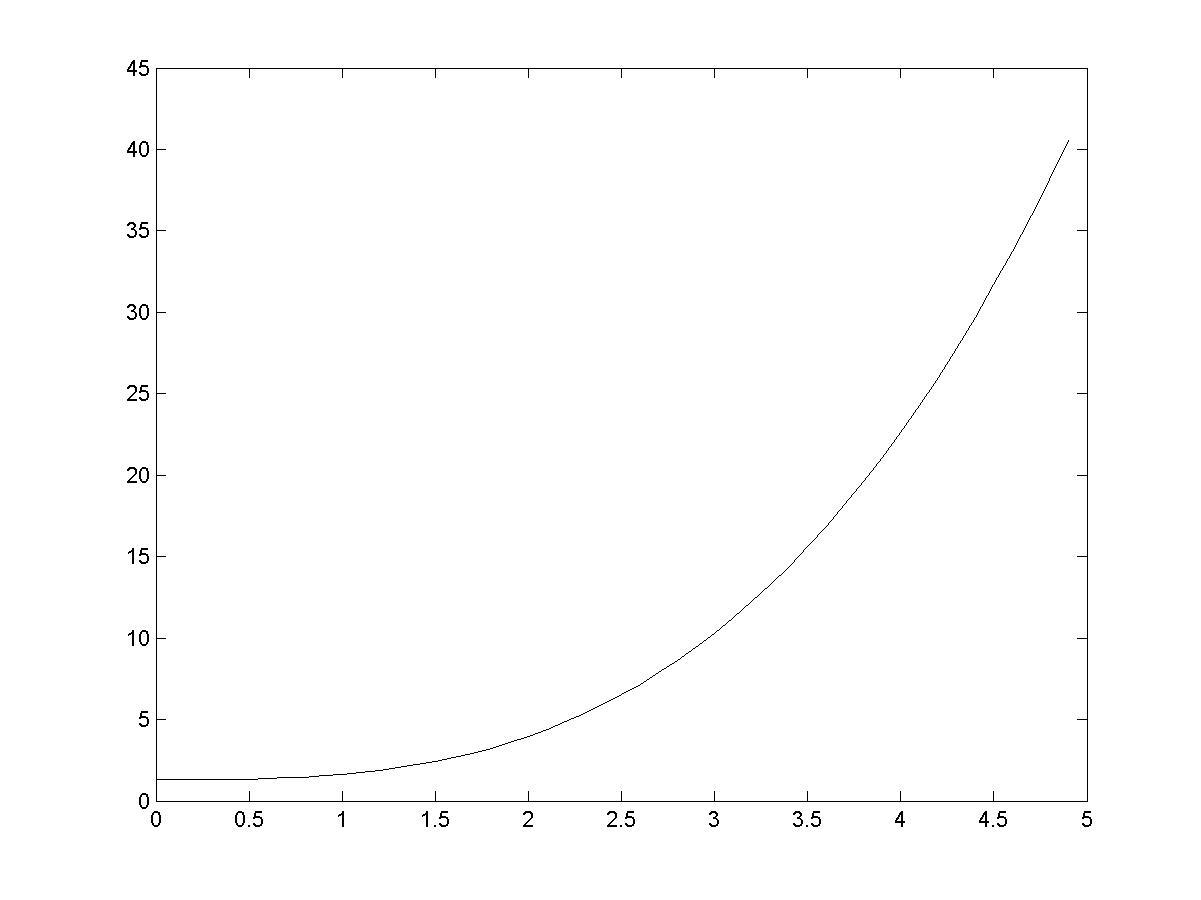
Рис. 9.4
% листинг файла EulerKoshi.m
function [X,Y]=EulerKoshi(y0,x0,x1,N)
dx=(x1-x0)/N;
x(1)=x0;
y(1)=y0;
for i=2:N
x(i)=x(1)+dx*(i-1);
Z=y(i-1)+dx*F9(x(i-1),y(i-1));
y(i)=y(i-1)+(F9(x(i-1),y(i-1))+F9(x(i),Z))*dx/2;
end;
X=x;
Y=y;
function z=F9(x,y)
z=x.^2;
Далее необходимо выполнить следующую последовательность команд:
>> x0=0; % левая граница отрезка интегрирования
>> x1=5; % правая граница отрезка интегрирования
>> y0=1.3; % начальное условие
>> N=50; % число узлов разбиения отрезка интегрирования
>> [X Y]=EulerKoshi(y0,x0,x1,N); % нахождение численного
% решения задачи Коши
>> i=1:length(X);
>> Z(i)=y0+1/3*X(i).^3; % вычисление значений точного решения
>> plot(X,Z,X,Y,':') % визуализация точного и численного решений
% (рис. 9.4)
>> plot(X,abs(Z-Y)) % визуализация разности между численным и
% точным решениями ДУ (9.5)
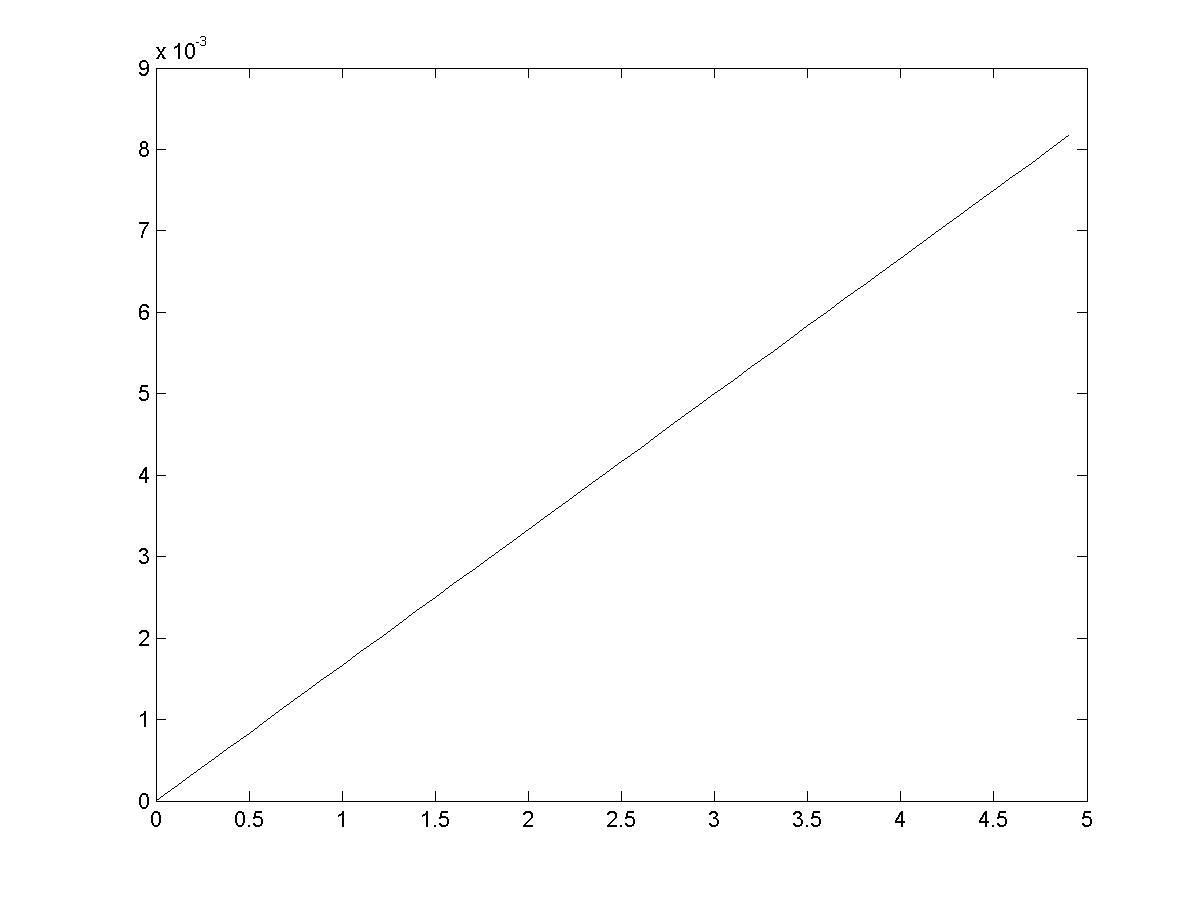
Рис. 9.5
Из сравнения рис. 9.3, 9.5 видно, что погрешность, как и ожидалось уменьшилась в 102 раз (h = 0.1).
