5.6. Решение задачи одномерной интерполяции средствами пакете matlab

Для решения задачи одномерной сплайн-интерполяции в пакете MATLAB используется функция interp1( ), имеющая следующий синтаксис:

yi = interp1(x,y,xi) % линейная интерполяция табличных значений

% x,y в точках, абсциссы которых находятся

% в векторе xi

yi = interp1(y,xi) % линейная интерполяция табличных значений y

% в точках, абсциссы которых находятся

% в векторе xi,

% в предположении, что x=1:length(y)

yi = interp1(x,y,xi,method) % интерполяция линейных значений с

% использованием выбранного метода

% интерполяции

Возможные значения переменной method:

'nearest' % интерполяция с использованием ближайших узлов

'linear' % линейная интерполяция (по умолчанию)

'spline' % интерполяция кубическим сплайном

'pchip' % интерполяция полиномами Эрмита третьей степени

'cubic' % аналогично pchip

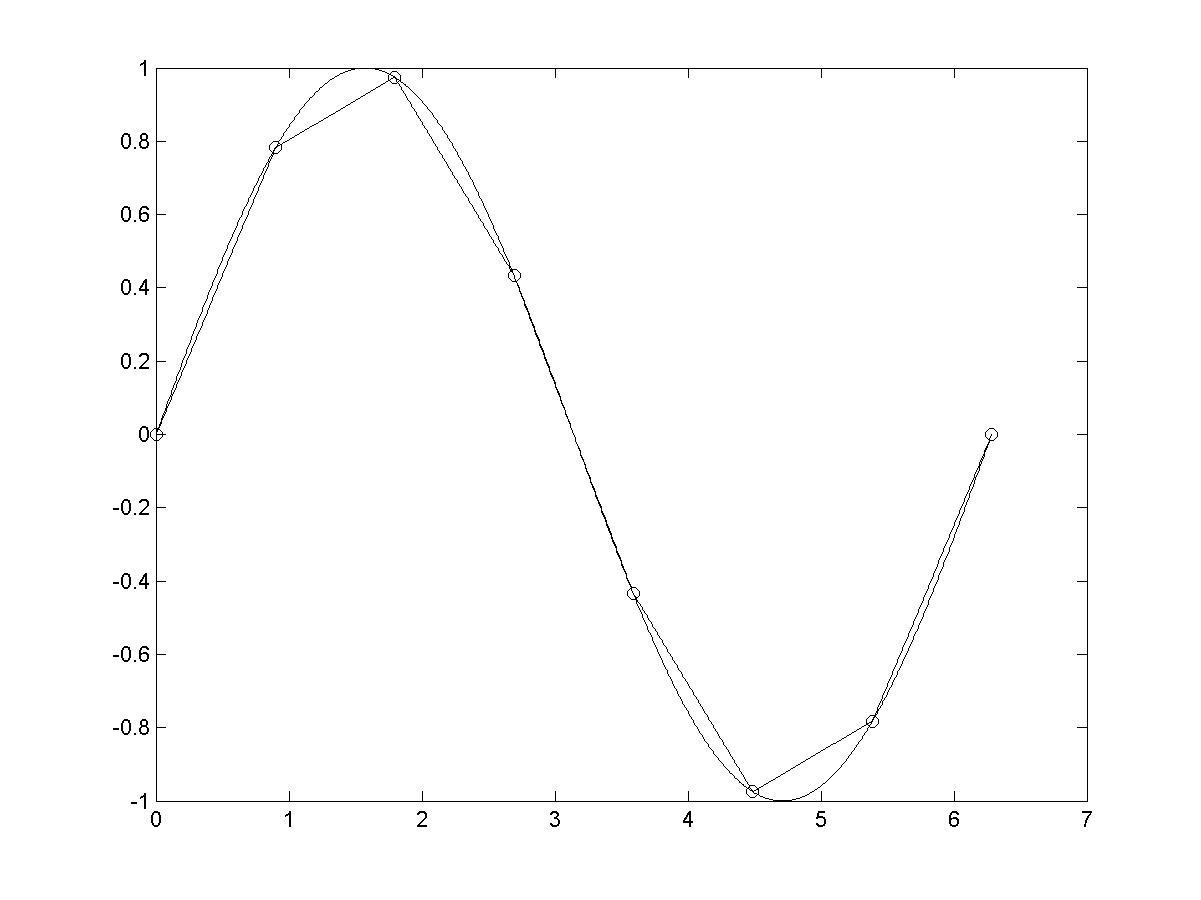
Рис. 5.10

Пример 5.1. Решение задачи интерполяции функции, заданной таблично средствами пакета MATLAB

1. Задание табличных значений интерполируемой функции

>> N=8;

>> i=1:N;

>> x(i)=2*pi/(N-1)*(i-1);

>> y=sin(x);

2. Задание значения абсцисс точек, в которых вычисляется значение интерполяционного полинома

>> M=1000;

>> j=1:M;

>> X(j)=2*pi/(M-1)*(j-1);

>> Y=sin(X); % вычисление точных значений интерполируемой

% функции

4. Вычисление интерполируемых значений функции в узлах координатной сетки и визуализация точного исходных данных, точных и интерполированных значений % рис. 5.10

>> yi=interp1(x,y,X);

>> plot(x,y,'o',X,Y,X,yi)

Лекция № 6. Численное дифференцирование

И ИНТЕГРИРОВАНИЕ

План

6.1. Численное дифференцирование функций, заданных аналитически

6.2. Особенности задачи численного дифференцирования функций, заданных таблично

6.3. Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)

6.4. Погрешность численного интегрирования

6.5. Вычисление интегралов методом Монте-Карло

6.1. Численное дифференцирование функций, заданных

аналитически

По определению производная функции

. (6.1)

Переходя в (6.1) от бесконечно малых к конечным разностям, получаем приближенную формулу численного дифференцирования

. (6.2)

Формула (6.2) позволяет построить простой вычислительный алгоритм:

1) Задать значение точки, в которой вычисляется производная.

2) Задать значение приращение .

3) Вычислить производную в соответствие с формулой (6.2).

Замена бесконечно-малых приращений конечными является причиной возникновения ошибки. Для оценки ее величины разложим функцию в точке в ряд Тэйлора

(6.3)

Подставив (6.3) в (6.4) и приведя подобные члены, получим

. (6.4)

Из (6.4) видно, что все члены начиная с со второго, определяют отличие численного значения производной от ее точного значения. Основной член погрешности равен , т.к. данный член, говорят, что формула (6.2) имеет первый порядок точности по.

Можно вычислять производную, используя симметричную разностную схему:

. (6.5)

Для оценки точности данной формулы необходимо удержать в разложении в ряд Тэйлора первые четыре члена:

. (6.6)

Раскрыв в (6.6) скобки и приведя подобные, получаем:

. (6.7)

Из (6.7) видно, что основной член погрешности равен , т.к. данный член ~, говорят, что формула (6.5) имеет второй порядок точности по.

Пример 6.1. Численное дифференцирование функции в пакетеMATLAB:

>> f=inline('sin(0.01*x.^2)'); % задание дифференцируемой

% функции

>> dx=0.01; % шаг изменения координатной сетки

>> x=0:dx:10*pi; % вычисление координат узлов

>> yf=feval(f,x); % вычисление значений функции в узлах

% выполнение процедуры численного дифференцирования

>> N=length(x);

>> m=1:N-1;

>> df(m)=yf(m+1)-yf(m)

>> plot(df) % визуализация производной функции (рис. 6.1)

>> f1=inline('0.02*x.*cos(0.01*x.^2)'); % задание функции,

% описывающей первую

% производную

>> ya=feval(f1,x); % вычисление значений первой производной по

% аналитической формуле

>> plot(x(m),abs(yf(m)-ya(m)); % визуализация разности между

% численными и аналитическими

% значениями производной (рис. 6.2)

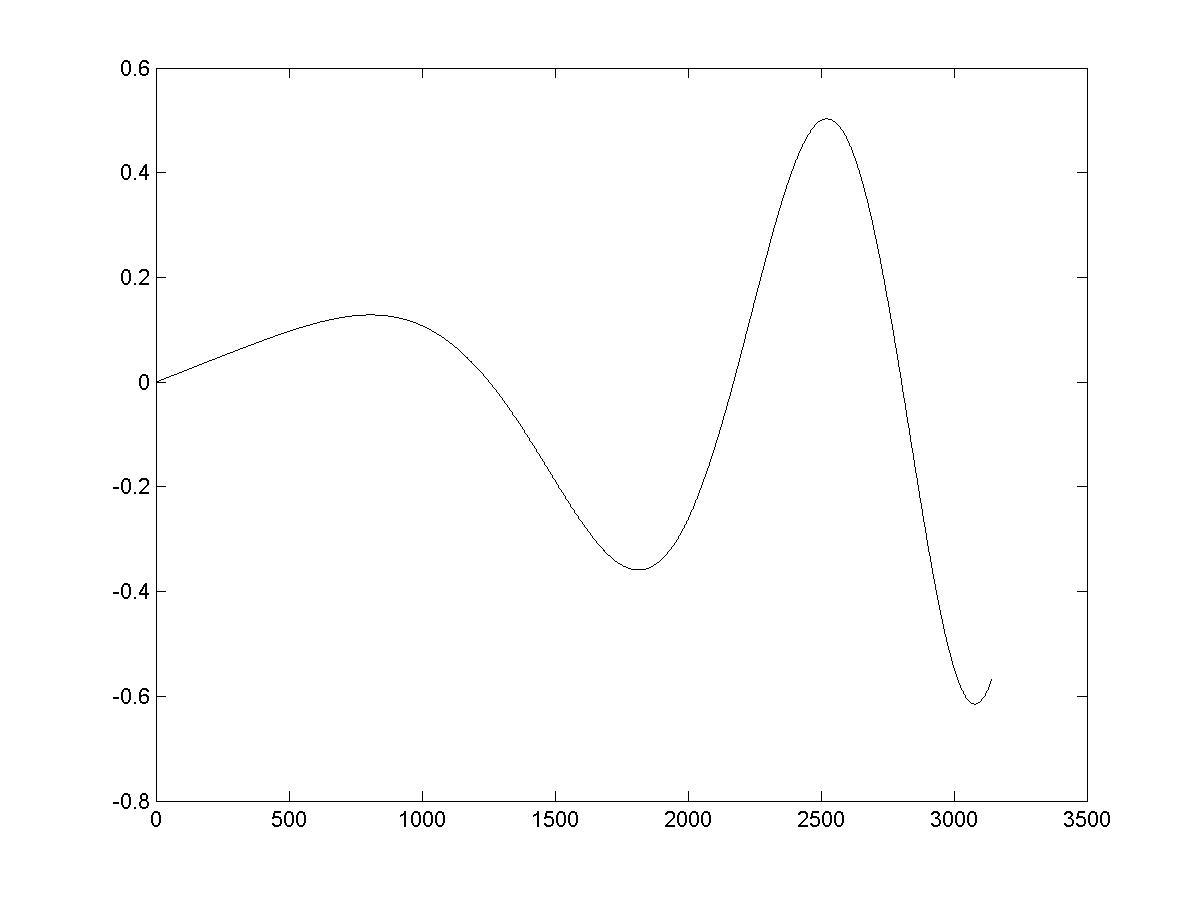
Рис. 6.1

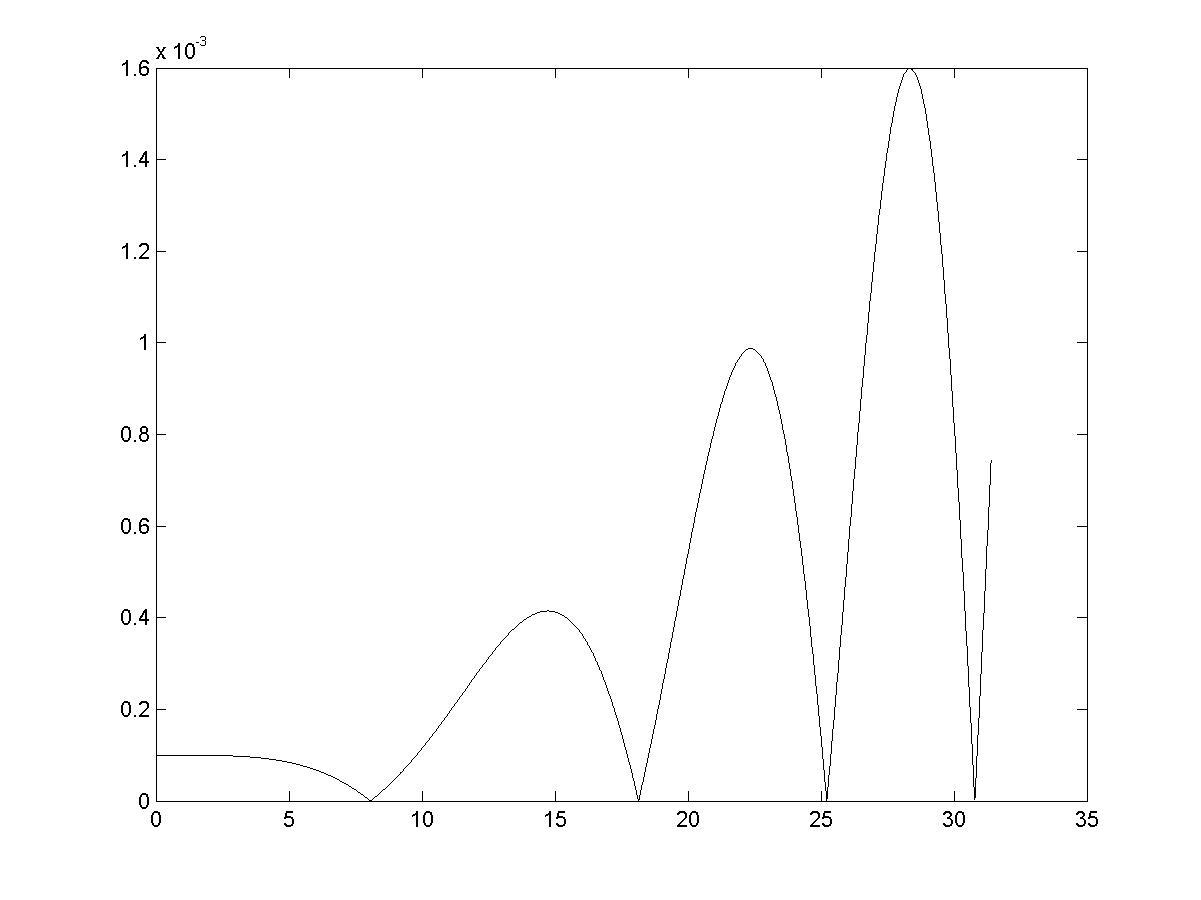
Рис. 6.2

Аналогичным образом поступают при вычислении производных высших порядков.

Отметим, что для аппроксимации производных конечными разностями в пакете MATLAB имеется функция diff( ).

Синтаксис функции:

>> diff(X) % возвращает конечные разности, вычисленные по

% смежным элементам вектора Х длина вектора,

% возвращаемого функцией diff(X) на единицу

% меньше длины вектора Х, если X  матрица

%, то возвращает матрицу, содержащую

% конечные разности, вычисленные по каждому столбцу

>> diff(X,n) % возвращает конечные разности n-го порядка

>> diff(X,n,dim) % возвращает конечные разности n-го порядка по

% столбцам (dim=1) или строкам матрицы