Лекция № 3. Методы решения систем линейных алгебраических уравнений План

3.1. Общие сведения и основные определения

3.2. Метод Гаусса и его реализация в пакете MATLAB

3.3. Вычисление определителей

3.4. Метод простой итерации. Достаточные условия сходимости итерационного процесса

3.5. Решение систем линейных уравнений методом Зейделя

3.6. Решение систем линейных уравнений средствами пакета MATLAB

3.1. Общие сведения и основные определения

Рассмотрим систему, состоящую из m линейных алгебраических уравнений с n неизвестными:

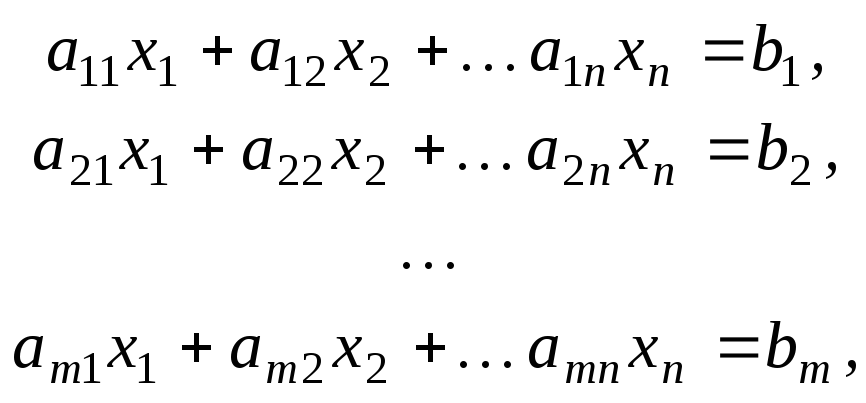(3.1)

которая может быть записана в матричном виде

, (3.2)

где А  прямоугольная матрица размерности mn

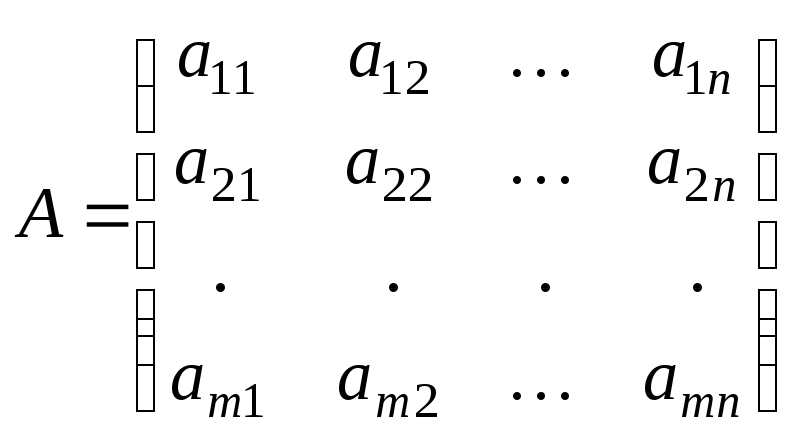, (3.3)

x  вектор n-го порядка

,

b  вектор m-порядка

.

Определение 3.1. Решением системы (3.1) называется такая упорядоченная совокупность чисел ,, …,, которая обращает все уравнения системы (3.1) в верные равенства.

Определение 3.2. Прямыми методами решения систем линейных уравнений называются  методы, дающие решение системы за конечное число арифметических операций. Если отсутствуют ошибки округления, то получаемые решения всегда являются точными.

Определение 3.3. Итерационными методами решения систем линейных называются методы, дающие решение системы уравнений как предел последовательности приближений, вычисляемых по единообразной схеме.

3.2. Метод Гаусса и его реализация в пакете matlab

Рассмотрим систему линейных алгебраических уравнений

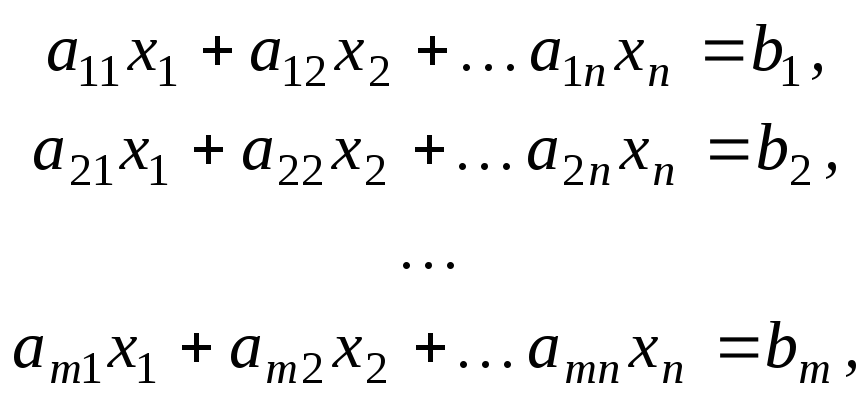(3.4)

при условии, что матрица A=(a_ij) невырождена.

Метод Гаусса состоит в преобразовании системы (3.4) последовательным исключением переменных к равносильной системе с треугольной матрицей

(3.5)

Затем из системы (3.5) последовательно находят значения всех неизвестных .

Т.о., процесс решения системы (3.4) распадается на два этапа:

1. Прямой ход  приведение системы (3.4) к треугольному виду.

2. Обратный ход  нахождение значений неизвестных переменных, в соответствие с (3.5).

Для реализации метод Гаусса в пакете MATLAB необходимо:

1. Создать файл Exchange.m, содержащий описание функции,осуществляющей перестановку строк при обнаружении в текущей строке нулевого элемента на главной диагонали.

% листинг файла Exchange.m

function z=Exchange(C,i)

k=i+1;

while C(k,i)==0

k=k+1;

end;

for j=1:size(C,1)

s=C(i,j);

C(i,j)=C(k,j);

C(k,j)=s;

end;

z=C;

2. Создание файла Simplex.m, содержащего описание функции, возвращающей расширенную матрицу системы к диагональному виду

% листинг файла Simplex.m

function z=Simplex(A,b)

N=size(A,1); % определение числа уравнений системы

C=cat(2,A,b); % создание расширенной матрицы системы

for i=1:N-1

if C(i,i)==0

C=Exchange(C,i);

end;

for j=0:N

C(i,N+1-j)=C(i,N+1-j)/C(i,i);

end;

for m=i+1:N

alpha=C(m,i);

for j=i:N+1

C(m,j)=C(m,j)-alpha*C(i,j);

end;

end;

end;

C(N,N+1)=C(N,N+1)/C(N,N);

C(N,N)=1;

z=C;

3. Создать файл Gauss.m, содержащий описание функции, возвращающей решение системы линейных уравнений методом Гаусса.

% листинг файла Gauss.m

function z=Gauss(A,b)

C=Simplex(A,b);

N=size(A,1);

v(N)=C(N,N+1);

for j=1:N-1

s=0;

for k=0:j-1

s=s+C(N-j,N-k)*v(N-k);

end;

v(N-j)=(C(N-j,N+1)-s)/C(N-j,N-j);

end;

z=v';

4. Задать матрицу системы линейных уравнений

>> A=[1,2,3,4,5;10,9,8,7,6;5,9,11,12,13;20,1,3,17,14;12,10,4,16,15]

A =

1 2 3 4 5

10 9 8 7 6

5 9 11 12 13

20 1 3 17 14

12 10 4 16 15

5. Задать вектор-столбец свободных членов

>> b=[10;20;30;40;50]

b =

10.0000

20.0000

30.0000

40.0000

50.0000

6. Решить систему уравнений, используя функцию Gauss( )

x=Gauss(A,b)

x =

0.0964

1.4324

-1.3530

1.6593

0.8921

7. Проверка правильности решения системы линейных уравнений

>> A*x

ans =

10.0000

20.0000

30.0000

40.0000

50.0000