Iteration Func-count f(X) step optimality cg-iterations

1 2 5 1 5 0

2 3 1 1 4 1

3 4 0.0026 0.223607 0.17 1

4 5 4.53076e-008 0.013546 0.00055 1

5 6 5.04984e-017 7.18272e-005 1.79e-008 1

Optimization terminated successfully:

Relative function value changing by less than OPTIONS.TolFun

Рассмотрим реализацию метода спуска средствами пакета MATLAB на примере рассмотренной выше в настоящем разделе системе нелинейных уравнений. Напомним, что для этого, следуя подходу, описанному в разделе 4.3, нужно из уравнений исходной системы создать новую положительно определенную функцию, минимум которой и будет искомым решением системы нелинейных уравнений. Следовательно, для нахождения решения рассматриваемой системы нелинейных уравнений необходимо выполнить следующую последовательность действий:

1. Создать файл F_sq.m, содержащий описание функции, возвращающей значения суммы квадратов функций и

% листинг файла F_sq.m²

function z=F_sq(x)

s=fm(x);

z=s(1,1).^2+s(2,1).^2;

2. Задать начальное приближение, в окрестности которого будет находиться минимум функции

>> x=[1;1];

3. Обратиться к встроенной функции fminsearch( )

>> fminsearch('F_sq',x)

ans =

0.8896

1.7913

Отметим, что способы обращения к функции fminsearch( ) и список ее формальных параметров аналогичны способам обращения к функции Fsolve( ) и списку ее формальных параметров.

Лекция № 5. Интерполирование функций План

5.1. Постановка задачи

5.2. Интерполяционный полином Лагранжа

5.3. Интерполяционный полином Ньютона для равноотстоящих узлов

5.3.1. Конечные разности

5.3.2. Первый интерполяционный полином Ньютона

5.3.3. Второй интерполяционный полином Ньютона

5.4. Погрешность метода многочленной интерполяции

5.5. Сплайн-интерполяция

5.6. Решение задачи одномерной интерполяции средствами пакете MATLAB

5.1. Постановка задачи

Пусть известные значения некоторой функции f(x) образуют следующую таблицу:

Таблица 5.1

x	x0	x1	…	xn
f(x)	y0	y1	…	yn

Требуется получить значение функции f(x) для значения аргумента xx₀,x_n, несовпадающего ни с одним из значений х_i (i = 0, 1,.., n).

Решение задачи находится отысканием некоторой приближающей функции f(X), близкой в некотором смысле к функции f(X), для которой известно аналитическое выражение/

Классический подход к решению задачи построения приближающей функции основан на требовании строгого совпадения значений функций f(x) и F(x) в точках

. (5.1)

В данном случае нахождение приближенной функции называется интерполированием, а точки называются узламиинтерполяции.

Будем искать интерполирующую функцию F(x) в виде многочлена степени n:

. (5.2)

Условия (5.1), наложенные на многочлен, позволяют однозначно определить его коэффициенты. Действительно, требуя для выполнения условий (5.1), получаем линейную систему, состоящую изуравнения:

. (5.3)

Решив систему (5.3) относительно неизвестных , находим значения этих неизвестных и, подставив в (5.2), находим аналитическое выражение аппроксимирующей функции.

Система (5.3) всегда имеет единственное решение, т. к. ее определитель

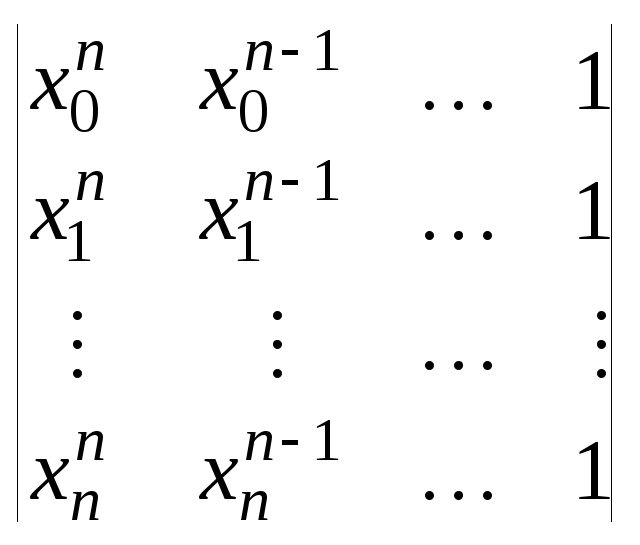, (5.4)

известный в алгебре как определитель Вандермонда, отличен от нуля.

Следовательно, интерполяционный многочлен существует и единственен.

Решение задачи интерполяции в пакете MATLAB с помощью полинома n-ой степени находится выполнением следующей последовательности команд:

1. Задать табличные значения интерполируемой функции

>> N=8;

>> i=1:N;

>> x(i)=2*pi/(N-1)*(i-1);

>> y=sin(x);

2. Выполнить визуализацию табличной зависимости и истинных значений функции (рис. 5.1)

>> M=1000;

>> j=1:M;

>> X(j)=2*pi/(M-1)*(j-1);

>> Y=sin(X);

>> plot(x,y,'o');

>> hold on

>> plot(X,Y)

Рис. 5.1

3. Создать файл Pol.m, содержащего описание функции, возвращающей значения полинома (5.2)

% листинг файла Pol.m

function z=Pol(x,a)

N=length(a);

M=length(x);

for j=1:M

s=0;

for i=1:N

s=s+a(i)*x(j).^(N-i);

end;

z(j)=s;

end;

4. Создать файл Vandermod.m, содержащий описание функции, возвращающей значения элементов матрицы Вандермонда

% листинг файла Vandermond.m

function z=Vandermond(x)

N=length(x);

z=ones(N,N);

for i=1:N

for j=1:N

z(i,j)=x(i).^(N-j);

end;

end;

5. Вычислить значения элементов матрицы Вандермонда

>> M=Vandermond(x);

6. Вычислить значения коэффициентов полинома

>> a=M^-1*y';

7. Вычислить значения полинома в заданных промежуточных точках

>> Y1=Pol(X,a);

8. Построить разность между точным и интерполированными значениями функции (рис. 5.2)

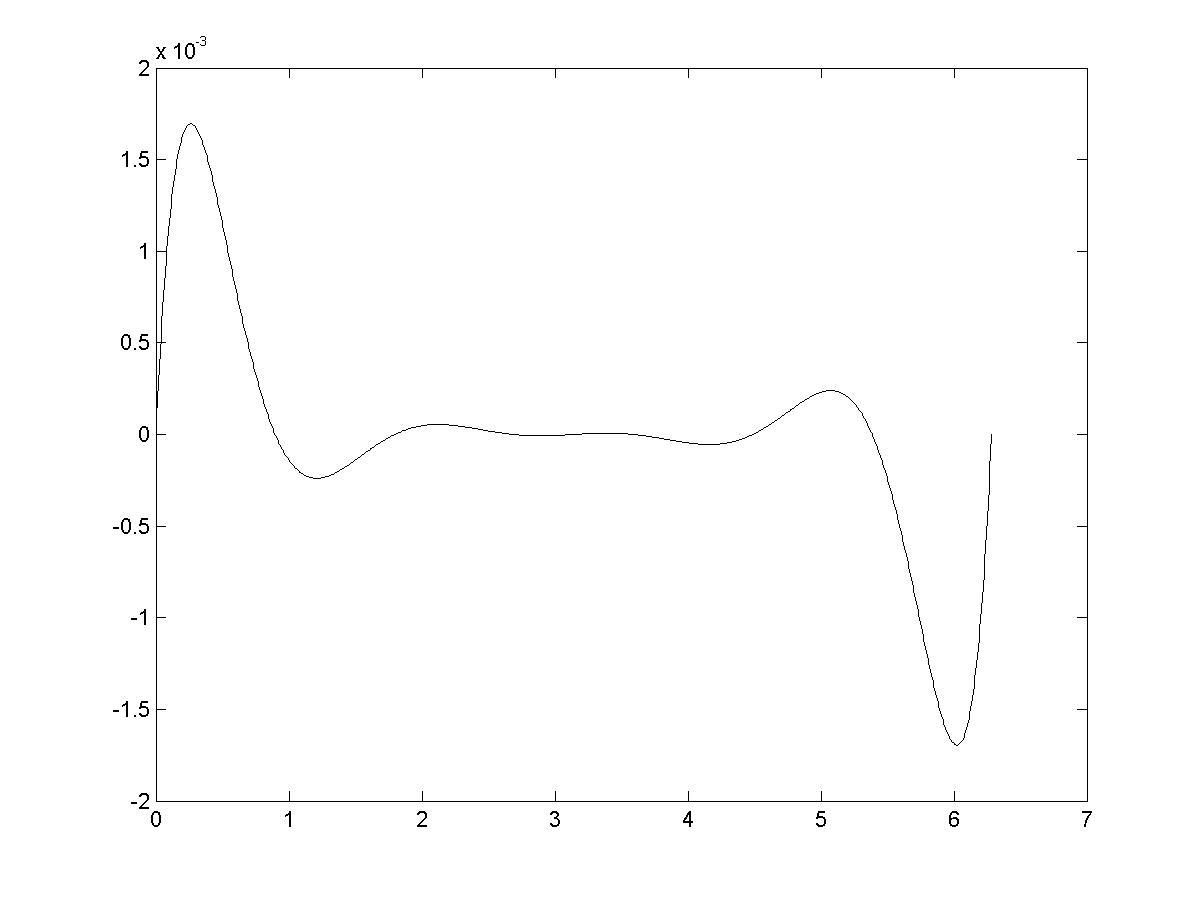
Рис. 5.2. Погрешность аппроксимации функции sin(x) полиномом 8-й степени