
- •Содержание
- •Лекция № 1. Теория погрешностей План
- •1.1. Источники и классификация погрешностей
- •1.2. Абсолютная и относительная погрешности. Формы записи данных
- •1.3. Вычислительная погрешность
- •2.1. Общие сведения и определения
- •2.2. Отделение корней
- •2.3. Метод половинного деления
- •2.4. Метод простой итерации
- •2.5. Преобразование уравнения к итерационному виду
- •2 0.777373 -3.32063 Search
- •Лекция № 3. Методы решения систем линейных алгебраических уравнений План
- •3.1. Общие сведения и основные определения
- •3.2. Метод Гаусса и его реализация в пакете matlab
- •3.3. Вычисление определителей
- •3.4. Решение систем линейных уравнений методом простой итерации
- •5. Метод Зейделя
- •3.6. Решение систем линейных уравнений средствами пакета matlab
- •Выражения
- •Лекция № 4. Методы решения систем нелинейных уравнений
- •4.2. Метод Ньютона решения систем нелинейных уравнений
- •Последовательные приближения корней
- •4.3. Решение нелинейных систем методами спуска
- •4.4. Решение систем нелинейных уравнений средствами пакета matlab
- •Iteration Func-count f(X) step optimality cg-iterations
- •Iteration Func-count f(X) step optimality cg-iterations
- •Лекция № 5. Интерполирование функций План
- •5.1. Постановка задачи
- •Решение задачи находится отысканием некоторой приближающей функции f(X), близкой в некотором смысле к функции f(X), для которой известно аналитическое выражение/
- •5.2. Интерполяционный полином Лагранжа
- •5.3. Интерполяционный полином Ньютона для равноотстоящих узлов
- •5.3.1. Конечные разности
- •5.3.2. Первая интерполяционная формула Ньютона
- •5.3.3. Вторая интерполяционная формула Ньютона
- •5.4. Погрешность интерполяции
- •5.5. Сплайн-интерполяция
- •5.6. Решение задачи одномерной интерполяции средствами пакете matlab
- •Лекция № 6. Численное дифференцирование
- •6.2. Особенности задачи численного дифференцирования функций, заданных таблично
- •6.3. Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)
- •6.4. Погрешность численного интегрирования
- •6.5. Вычисление интегралов методом Монте-Карло
- •Лекция № 7. Методы обработки экспериментальных данных План
- •7.1. Метод наименьших квадратов
- •Сумма квадратов отклонений
- •7.2. Нахождение приближающей функции в виде линейной функции и квадратичного трехчлена
- •7.5. Аппроксимация функцией произвольного вида
- •Лекция № 8. Преобразование Фурье
- •8.2. Эффект Гиббса
- •8.3. Спектральный анализ дискретных функций конечной длительности
- •8.4. Быстрое преобразование Фурье
- •Лекция № 9. Численные методы решения обыкновенных дифференциальных уравнений План
- •9.1. Основные сведения и определения
- •9.2. Метод Пикара
- •9.3. Метод Эйлера
- •9.4. Метод Рунге-Кутта
- •9.5. Средства пакета matlab для решения обыкновенных дифференциальных уравнений
9.4. Метод Рунге-Кутта
Метод Эйлера и метод Эйлера относятся к семейству методов Рунге-Кутта. Для построения данных методов можно использовать следующий общий подход. Фиксируем некоторые числа:
![]() .
.
Последовательно вычисляем:
![]() ,
,
![]() ,
,
…
![]()
и полагаем:
![]() .
(9.28)
.
(9.28)
Рассмотрим
вопрос о выборе параметров
![]() .
Обозначим
.
Обозначим
![]() .
.
Будем предполагать, что
![]() ,
,
а
![]() для некоторой функции
для некоторой функции![]() .
.
По формуле Тэйлора справедливо равенство
![]() ,
(9.29)
,
(9.29)
где
![]() .
.
При
![]() будем иметь:
будем иметь:
![]()
![]()
![]() ,
,
![]() .
.
Ясно,
что равенство
![]() выполняется для любых функций
выполняется для любых функций![]() лишь при условии, что
лишь при условии, что![]() При данном значении
При данном значении![]() из формулы (9.28) получаются формулы
(9.24), (9.25) метода Эйлера. Погрешность
данного метода на шаге согласно (9.29)
равна
из формулы (9.28) получаются формулы
(9.24), (9.25) метода Эйлера. Погрешность
данного метода на шаге согласно (9.29)
равна
![]() .
.
Рассмотрим
случай
![]() ,
тогда
,
тогда
![]() ,
,
где
![]() .
.
Согласно исходному дифференциальному уравнению
![]()
![]()
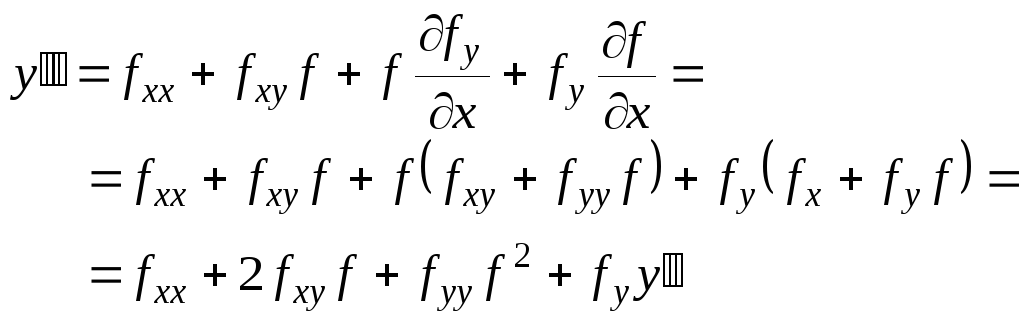 (9.30)
(9.30)
Вычисляя
производные функции
![]() и, подставляя в выражения для
и, подставляя в выражения для![]() значение
значение![]() ,
получаем
,
получаем
![]()
![]() ,
,
![]() .
(9.31)
.
(9.31)
Требование
![]()
будет
выполняться для всех
![]() только в том случае, если одновременно
справедливы следующие три равенства
относительно четырех параметров:
только в том случае, если одновременно
справедливы следующие три равенства
относительно четырех параметров:
![]() ,
,
![]() ,
(9.32)
,
(9.32)
![]()
Задавая
произвольно значения одного из параметров
и определяя значения остальных из
системы (9.32), можно получать различные
методы Рунге-Кутта с порядком погрешности
![]() .
Например, при
.
Например, при![]() из (9.32) получаем:
из (9.32) получаем:![]()
![]() ,
,![]() .
.
Для выбранных значений параметров (9.28) приобретает следующий вид:
![]() .
.
(Здесь
![]() записано вместо
записано вместо![]() ,
,![]()
вместо
вместо
![]() ,
а через
,
а через![]() обозначено выражение
обозначено выражение![]() .)
.)
Таким образом, для рассматриваемого случая приходим к расчетным формулам (9.27) метода Эйлера-Коши. Из (9.29) следует, что главная часть погрешности на шаге есть
![]() ,
,
т.е. погрешность пропорциональна третьей степени шага.
На
практике наиболее часто используют
метод Рунге-Кутта с
![]() .
Данный метод реализуются в соответствие
со следующими расчетными формулами:
.
Данный метод реализуются в соответствие
со следующими расчетными формулами:
![]()
![]()
![]() (9.33)
(9.33)
![]()
![]() .
.
Погрешность рассматриваемого метода Рунге-Кутта на шаге пропорциональна пятой степени шага.
Геометрический
смысл использования метода Рунге-Кутта
с расчетными формулами состоит в
следующем. Из точки
![]() сдвигаются в направлении, определяемом
углом
сдвигаются в направлении, определяемом
углом![]() ,
для которого
,
для которого![]() .
На этом направлении выбирается точка
с координатами
.
На этом направлении выбирается точка
с координатами![]() .
Затем из точки
.
Затем из точки![]() сдвигаются в направлении, определяемым
углом
сдвигаются в направлении, определяемым
углом![]() ,
для которого
,
для которого![]() ,
и на этом направлении выбирается точка
с координатами
,
и на этом направлении выбирается точка
с координатами![]() .
Наконец из точки
.
Наконец из точки![]() ,
сдвигаются в направлении, определяемом
углом
,
сдвигаются в направлении, определяемом
углом![]() ,
для которого
,
для которого![]() и на этом направлении выбирается точка
с координатами
и на этом направлении выбирается точка
с координатами![]() .
Этим задается еще одно направление,
определяемое углом
.
Этим задается еще одно направление,
определяемое углом![]() ,
для которого
,
для которого![]() .
Четыре, полученные направления усредняются
в соответствие с (9.33). На этом окончательном
направлении и выбирается очередная
точка
.
Четыре, полученные направления усредняются
в соответствие с (9.33). На этом окончательном
направлении и выбирается очередная
точка![]() .
.
Пример 9.2. Найти решение задачи Коши дифференциального уравнения
![]() ,
,
![]()
методом Рунге-Кутта четвертого порядка.
Для нахождения решения данного ДУ необходимо создать файл RungeKutt4.m, содержащий описание функции, возвращающей решение дифференциального уравнения методом Рунге-Кутта четвертого порядка.
% листинг файла RungeKutt4.m
function [X,Y]=RungeKutt4(y0,x0,x1,N)
dx=(x1-x0)/N;
x(1)=x0;
y(1)=y0;
for i=2:N
x(i)=x(1)+dx*(i-1);
k1=dx*F9(x(i-1),y(i-1));
k2=dx*F9(x(i-1)+dx/2,y(i-1)+k1/2);
k3=dx*F9(x(i-1)+dx/2,y(i-1)+k2/2);
k4=dx*F9(x(i-1)+dx,y(i-1)+k3);
y(i)=y(i-1)+1/6*(k1+2*k2+2*k3+k4);
end;
X=x;
Y=y;
function z=F9(x,y)
z=x.^2;
Далее необходимо выполнить следующую последовательность команд:
>> x0=0; % левая граница отрезка интегрирования
>> x1=5; % правая граница отрезка интегрирования
>> y0=1.3; % начальное условие
>> N=50; % число узлов разбиения отрезка интегрирования
>> [X Y]=RungeKutt4(y0,x0,x1,N); % нахождение численного
% решения задачи Коши
>> i=1:length(X);
>> Z(i)=y0+1/3*X(i).^3; % вычисление значений точного решения
>> plot(X,Z,X,Y,':') % визуализация точного и численного решений
% (рис. 9.6)
>> plot(X,abs(Z-Y)) % визуализация разности между численным и
% точным решениями ДУ (9.7)
