
- •Содержание
- •Лекция № 1. Теория погрешностей План
- •1.1. Источники и классификация погрешностей
- •1.2. Абсолютная и относительная погрешности. Формы записи данных
- •1.3. Вычислительная погрешность
- •2.1. Общие сведения и определения
- •2.2. Отделение корней
- •2.3. Метод половинного деления
- •2.4. Метод простой итерации
- •2.5. Преобразование уравнения к итерационному виду
- •2 0.777373 -3.32063 Search
- •Лекция № 3. Методы решения систем линейных алгебраических уравнений План
- •3.1. Общие сведения и основные определения
- •3.2. Метод Гаусса и его реализация в пакете matlab
- •3.3. Вычисление определителей
- •3.4. Решение систем линейных уравнений методом простой итерации
- •5. Метод Зейделя
- •3.6. Решение систем линейных уравнений средствами пакета matlab
- •Выражения
- •Лекция № 4. Методы решения систем нелинейных уравнений
- •4.2. Метод Ньютона решения систем нелинейных уравнений
- •Последовательные приближения корней
- •4.3. Решение нелинейных систем методами спуска
- •4.4. Решение систем нелинейных уравнений средствами пакета matlab
- •Iteration Func-count f(X) step optimality cg-iterations
- •Iteration Func-count f(X) step optimality cg-iterations
- •Лекция № 5. Интерполирование функций План
- •5.1. Постановка задачи
- •Решение задачи находится отысканием некоторой приближающей функции f(X), близкой в некотором смысле к функции f(X), для которой известно аналитическое выражение/
- •5.2. Интерполяционный полином Лагранжа
- •5.3. Интерполяционный полином Ньютона для равноотстоящих узлов
- •5.3.1. Конечные разности
- •5.3.2. Первая интерполяционная формула Ньютона
- •5.3.3. Вторая интерполяционная формула Ньютона
- •5.4. Погрешность интерполяции
- •5.5. Сплайн-интерполяция
- •5.6. Решение задачи одномерной интерполяции средствами пакете matlab
- •Лекция № 6. Численное дифференцирование
- •6.2. Особенности задачи численного дифференцирования функций, заданных таблично
- •6.3. Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)
- •6.4. Погрешность численного интегрирования
- •6.5. Вычисление интегралов методом Монте-Карло
- •Лекция № 7. Методы обработки экспериментальных данных План
- •7.1. Метод наименьших квадратов
- •Сумма квадратов отклонений
- •7.2. Нахождение приближающей функции в виде линейной функции и квадратичного трехчлена
- •7.5. Аппроксимация функцией произвольного вида
- •Лекция № 8. Преобразование Фурье
- •8.2. Эффект Гиббса
- •8.3. Спектральный анализ дискретных функций конечной длительности
- •8.4. Быстрое преобразование Фурье
- •Лекция № 9. Численные методы решения обыкновенных дифференциальных уравнений План
- •9.1. Основные сведения и определения
- •9.2. Метод Пикара
- •9.3. Метод Эйлера
- •9.4. Метод Рунге-Кутта
- •9.5. Средства пакета matlab для решения обыкновенных дифференциальных уравнений
6.5. Вычисление интегралов методом Монте-Карло
Проиллюстрируем
идеи метода Монте-Карло на примере
вычисления определенного интеграла от
функции, зависящей от одной переменной.
Пусть нам необходимо вычислить интеграл
(6.11) от некоторой заданной функции
![]() на интервале
на интервале![]() .
В предыдущем разделе мы рассмотрели
несколько различных формул интегрирования,
в которых использовались значения
функции
.
В предыдущем разделе мы рассмотрели
несколько различных формул интегрирования,
в которых использовались значения
функции![]() ,
вычисляемые в равноотстоящих точках.
Однако можно использовать и другой
подход, суть которого легко понять из
следующего примера.
,
вычисляемые в равноотстоящих точках.
Однако можно использовать и другой
подход, суть которого легко понять из
следующего примера.
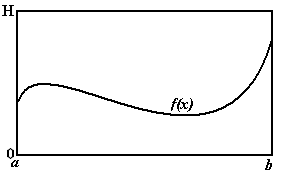
Рис. 6.6
Представим
себе прямоугольник высотой H
и длиной b a
такой, что функция
![]() целиком лежит внутри данного прямоугольника
(рис. 6.6). СгенерируемN
пар случайных чисел, равномерно
распределенных в данном прямоугольнике:
целиком лежит внутри данного прямоугольника
(рис. 6.6). СгенерируемN
пар случайных чисел, равномерно
распределенных в данном прямоугольнике:
![]() ,
,![]() .
(6.29)
.
(6.29)
Тогда
доля точек
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию![]() ,
является оценкой отношения интеграла
от функции
,
является оценкой отношения интеграла
от функции![]() к площади рассматриваемого прямоугольника.
Следовательно, оценка интеграла в данном
методе может быть получена по формуле
к площади рассматриваемого прямоугольника.
Следовательно, оценка интеграла в данном
методе может быть получена по формуле
![]() ,
(6.30)
,
(6.30)
где
![]()
число точек, удовлетворяющих условию
число точек, удовлетворяющих условию
![]() ,N
полное количество точек, A
площадь прямоугольника.
,N
полное количество точек, A
площадь прямоугольника.
Можно
предложить и другой путь вычисления
определенного интеграла, рассматривая
его как среднее значение функции
![]() на отрезке
на отрезке![]() :
:
![]() ,
(6.31)
,
(6.31)
где
![]()
последовательность случайных чисел с
равномерным законом распределения на
отрезке
последовательность случайных чисел с
равномерным законом распределения на
отрезке
![]() .
.
Отметим,
что в отличие от данных методов погрешность
метода Монте-Карло не зависит от
размерности и меняется как
![]() .
Следовательно, для достаточно большихd
интегрирование по методу Монте-Карло
будет приводить к меньшим погрешностям
при тех же значениях N.
.
Следовательно, для достаточно большихd
интегрирование по методу Монте-Карло
будет приводить к меньшим погрешностям
при тех же значениях N.
Пример
6.6. Вычисление
интеграла
![]() методом Монте-Карло в пакетеMATLAB:
методом Монте-Карло в пакетеMATLAB:
% задание координат вершит прямоугольника
>> Xmin=0;
>> Xmax=pi/2;
>> Ymin=0;
>> Ymax=1.5;
% генерация случайных координат
>> N=2000;
>> x=Xmin+(Xmax-Xmin)*rand(N,1);
>> y=Ymin+(Ymax-Ymin)*rand(N,1);
% подсчет числа точек, попавших под график функции
>> s=0;
>> for i=1:N
if y(i)<=feval(f,x(i))
s=s+1;
end;
end;
>> s*(Xmax-Xmin)*(Ymax-Ymin)/N % вычисление значения
% интеграла
ans =
1.0261
% вычисление интеграла в соответствие с (6.31)
>> Fr=feval(f,x);
>> (Xmax-Xmin)/N*sum(Fr)
ans =
1.0091
Лекция № 7. Методы обработки экспериментальных данных План
7.1. Метод наименьших квадратов
7.2. Нахождение приближающей функции в виде линейной функции и квадратичного трехчлена
7.3. Нахождение приближающей функции в виде других элементарных функций
7.4. Аппроксимация линейной комбинацией функций
7.5. Аппроксимация функцией произвольного вида
7.1. Метод наименьших квадратов
Пусть
в результате измерений в процессе опыта
получена таблица некоторой зависимости
![]() (табл. 7.1).
(табл. 7.1).
Таблица 7.1
|
x |
|
|
… |
|
|
f(x) |
|
|
… |
|
Требуется найти формулу, выражающую данную зависимость аналитически.
Один
из подходов к решению данной задачи
состоит в построении интерполяционного
многочлена, значения которого будут в
точках
![]() ,
,![]() ,…,
,…,![]() совпадать с соответствующими значениями
совпадать с соответствующими значениями![]() из табл. 7.1. Однако совпадение значений
в узлах может вовсе не означать совпадения
характеров исходной и интерполирующей
функций. Требование неукоснительного
совпадения значений, тем более
неоправданно, если значения функций
из табл. 7.1. Однако совпадение значений
в узлах может вовсе не означать совпадения
характеров исходной и интерполирующей
функций. Требование неукоснительного
совпадения значений, тем более
неоправданно, если значения функций![]() известны с некоторой погрешностью (рис.
7.1).
известны с некоторой погрешностью (рис.
7.1).
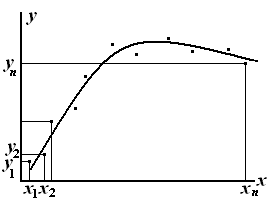
Рис. 7.1
Поставим задачу так, чтобы с самого начала обязательно учитывался характер исходной функции: найти функцию заданного вида
![]() ,
(7.1)
,
(7.1)
которая
в точках
![]() ,
,![]() ,…,
,…,![]() принимает значения как можно более
близкие к табличным значениям
принимает значения как можно более
близкие к табличным значениям
![]() ,
,
![]() ,…,
,…,![]() .
.
Следует отметить, что строгая функциональная зависимость для табл. 7.1. наблюдается редко, т. к. каждая из входящих в нее величин может зависеть от многих случайных факторов, поэтому обычно используют простые по виду аналитические функции.
Рассмотрим
один из наиболее распространенных
способов нахождения функции
![]() .
Предположим, что приближающая функция
.
Предположим, что приближающая функция![]() в точках
в точках![]() ,
,![]() ,…,
,…,![]() имеет значения
имеет значения
![]() ,
,
![]() ,…,
,…,![]() .
(7.2)
.
(7.2)
Требование
близости табличных значений
![]() ,
,
![]() ,…,
,…,![]() и значений (7.2) можно истолковать следующим
образом. Будем рассматривать совокупность
значений функции
и значений (7.2) можно истолковать следующим
образом. Будем рассматривать совокупность
значений функции![]() из табл. 7.1 и совокупность значений (7.2)
как координаты двух точекn-мерного
пространства. С учетом этого задача
приближения функции может быть
переформулирована следующим образом:
найти такую функцию
из табл. 7.1 и совокупность значений (7.2)
как координаты двух точекn-мерного
пространства. С учетом этого задача
приближения функции может быть
переформулирована следующим образом:
найти такую функцию
![]() заданного вида, чтобы расстояние между
точками
заданного вида, чтобы расстояние между
точками
![]() и
и
![]() было наименьшим. Воспользовавшись
метрикой Евклидова пространства,
приходим к требованию, чтобы величина
было наименьшим. Воспользовавшись
метрикой Евклидова пространства,
приходим к требованию, чтобы величина
![]() ,
(7.3)
,
(7.3)
была наименьшей. Это равносильно следующему: сумма квадратов
![]() (7.4)
(7.4)
должна быть наименьшей.
Таблица 7.2
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно
задача приближения функции
![]() теперь формулируется следующим образом:
для функции
теперь формулируется следующим образом:
для функции![]() ,
заданной табл. 7.1, найти функцию
,
заданной табл. 7.1, найти функцию![]() определенного вида так, чтобы сумма
квадратов (7.4) была наименьшей. Эта задача
называется приближением функции методом
наименьших квадратов. В качестве
приближающих функций в зависимости от
характера точечного графика функции
определенного вида так, чтобы сумма
квадратов (7.4) была наименьшей. Эта задача
называется приближением функции методом
наименьших квадратов. В качестве
приближающих функций в зависимости от
характера точечного графика функции![]() часто используют функции, представленные
в табл. 7.2. (Здесьa,
b,
m
неизвестные параметры)
часто используют функции, представленные
в табл. 7.2. (Здесьa,
b,
m
неизвестные параметры)
Когда вид приближающей функции установлен, задача сводится к отысканию значений параметров.
Рассмотрим метод нахождения параметров приближающей функции в общем виде на примере приближающей функции, зависящей от трех параметров:
![]() .
(7.5)
.
(7.5)
Имеем
![]() ,
(7.6)
,
(7.6)
Сумма
квадратов разностей соответствующих
значений функций
![]() и
и![]() имеет вид:
имеет вид:
![]() .
(7.7)
.
(7.7)
Сумма
является функцией
![]() трех переменных. Используя необходимое
условие экстремума:
трех переменных. Используя необходимое
условие экстремума:
![]() ,
,
получаем систему уравнений
![]() ,
,
![]() ,
(7.8)
,
(7.8)
![]() .
.
Решив
систему (7.8) относительно параметров a,
b,
c,
получаем конкретный вид функции
![]() .
Изменение количества параметров не
приведет к изменению сути самого подхода,
а выразится в изменении количества
уравнений в системе (7.8).
.
Изменение количества параметров не
приведет к изменению сути самого подхода,
а выразится в изменении количества
уравнений в системе (7.8).
Значения разностей
![]() (7.9)
(7.9)
называют отклонениями измеренных значений от вычисленных по формуле (7.5).
