9.5. Средства пакета matlab для решения обыкновенных дифференциальных уравнений
Метод Рунге-Кутта 4-го порядка решение задачи Коши для ДУ в пакете MATLAB реализован в виде функции ode45. Данный метод рекомендуется использовать при первой попытке нахождения численного решения задачи.
Помимо данной функции в пакете MATLAB реализованы и другие
Рис. 9.6
Рис. 9.7
методы решения дифференциальных уравнений и систем ДУ:
ode23 функция реализует одношаговые явные методы Рунге-Кутта (2 и 3) порядков. Функция используется при решении нежестких систем ДУ обеспечивает удовлетворительную точность при меньших нежели функция ode45 временных затратах.
ode113 функция реализует многошаговый метод Адамса-Башворта-Мултона переменного порядка. Функция используется при необходимости обеспечить высокую точность численного решения.
ode15s функция реализует многошаговый метод переменного порядка (от 1 до 5 по умолчанию), основанный на формулах численного дифференцирования. Данный метод следует использовать в том случае, если не удается найти численное решение с помощью функции ode45.
ode23s функция реализует одношаговый метод, использующий модифицированную формулу Розенброка 2-го порядка. Данной метод обеспечивает более высокую скорость вычислений по сравнению с другими методами при сравнении с другими методами при относительно более низкой точности вычислений.
ode23t функция реализует метод трапеций с интерполяцией. Данный метод используют при решении уравнений, описывающих колебательные системы с почти гармоническим выходным сигналом.
ode23tb функция реализует неявный метод Рунге-Кутта в начале интервала интегрирования и далее метод, использующий формулы обратного дифференцирования 2-го порядка. Данный метод обладает большей скорость нежели метод ode15s при, соответственно, меньшей точности.
Все перечисленные
выше функции, называемые в документации
пакета Solver
(решатель), могут решать системы ДУ
явного вида
.
Кроме того решателиode15s,
ode23s,
ode23t
и ode23tb
системы
дифференциальных уравнений неявного
вида
,
а также все решатели, кромеode23s,
могут находить решения уравнения вида
.
Пример 9.3. Решение задачи Коши для дифференциального уравнения
,
T(0)=80.
где Ts, r заданные постоянные, имеющие физический смысл температуры окружающей среды и коэффициента остывания, соответственно,
Для решения дифференциального уравнения (2.1) сначала создаем m-файл, содержащий определение функции, стоящей в правой части уравнения (2.1):
function Z=Tempr(t,T)
% определение функции, стоящей в правой части уравнения (2.1)
global Ts r
Z(1)=-r*(T-Ts);
который сохраним на диске под именем Tempr.m.
Далее необходимо выполнить в командном окне следующую последовательность операторов:
>> global Ts r % объявление глобальных переменных
>> Ts = 22 % задание значения температуры окружающей среды
>> r = 0.024 % задание значения коэффициента остывания
>> T0 = 80 % задание начальной температуры тела
>> [t,T]=ode45('Tempr',[0:0.01:15],T0); % Tempr имя файла,
% содержащего
% определение функции,
% стоящей в правой части
% уравнения (2.1);
% [0:0.01:15] вектор,
% определяющий интервал
% интегрирования,
% T0 вектор
% начальных условий
>> plot(t,T)
После выполнения приведенной выше последовательности команд будет создано окно, содержащее график зависимости температуры тела от времени, представленный на рис. 9.8.
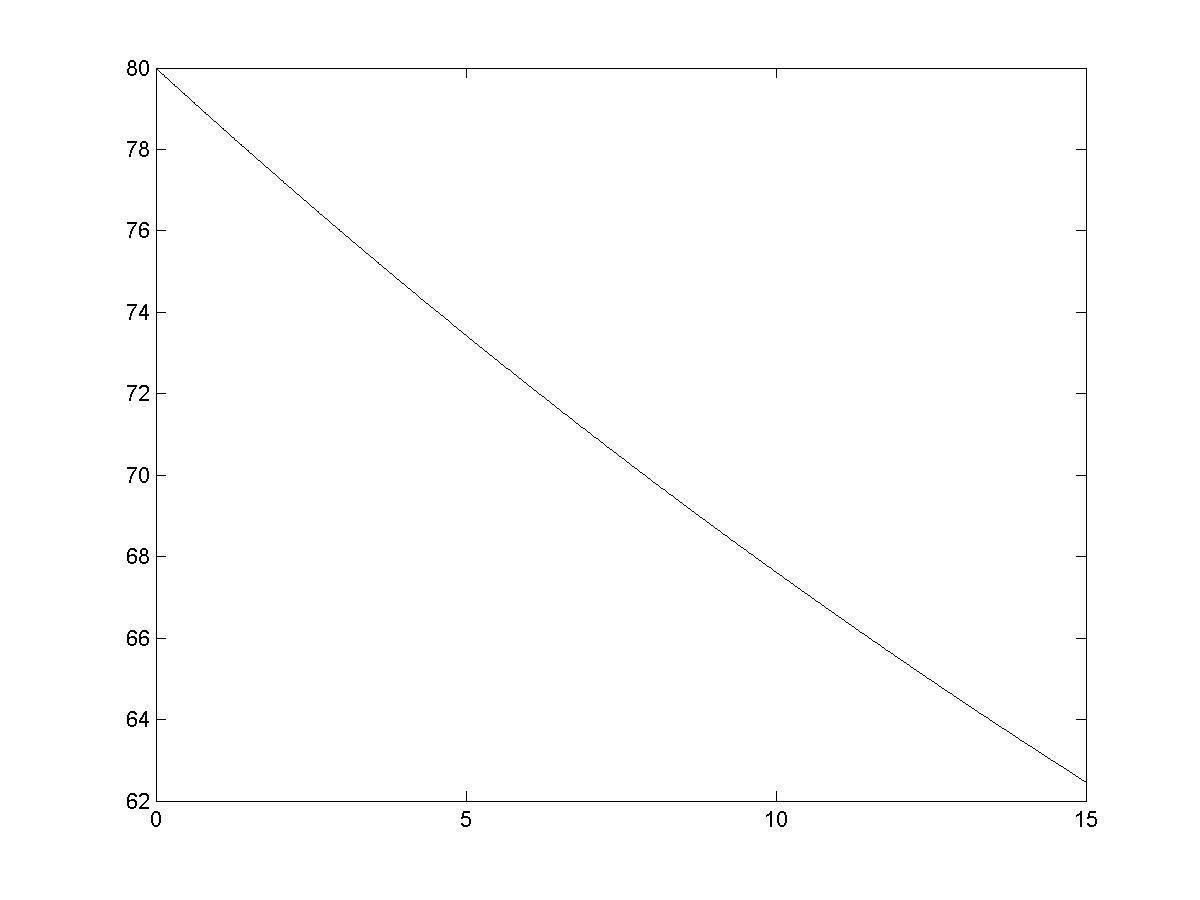
Рис. 9.8. Численное решение уравнения теплопроводности, возвращенное функцией ode45
По умолчанию решатели систем ДУ пакета MATLAB используют параметры, относительная погрешность которых не превосходит переменной RelTol = 10-3 , граница абсолютной погрешности численного решения переменная AbsTol равна 10-6. Для изменения значений этих переменных используется команда
>> options = odeset('RelTol',1e-4,'AbsTol',1e-4);
предваряющая команду вызова функции решателя системы ДУ.
1 Порядком сходимости последовательности (xk) к x* называют такое число p, что
,
где С > 0, при всех k > k0.
2 Здесь мы предполагаем, что ранее файл fm.m, содержащий описание функции, возвращающей значения функций f(x,y) и g(x,y) уже создан.