7.2 Сравнение дисперсий 2-ух совокупностей.

Пусть имеются две нормально распределенные совокупности, дисперсии которых равны ;нулевая гипотеза .

Так как дисперсии генеральных совокупностей неизвестны, проверка гипотезы осуществляется на основе сопоставления выборочных дисперсий и. Если отношение: близко к 1, нет оснований отклонять нулевую гипотезу, если значительно отличается – гипотеза отклоняется. Для решения вопроса, насколько большим должно быть отличие выборочных дисперсий, чтобы отклонение нулевой гипотезы было достаточно обоснованным, используется отношение

; ()

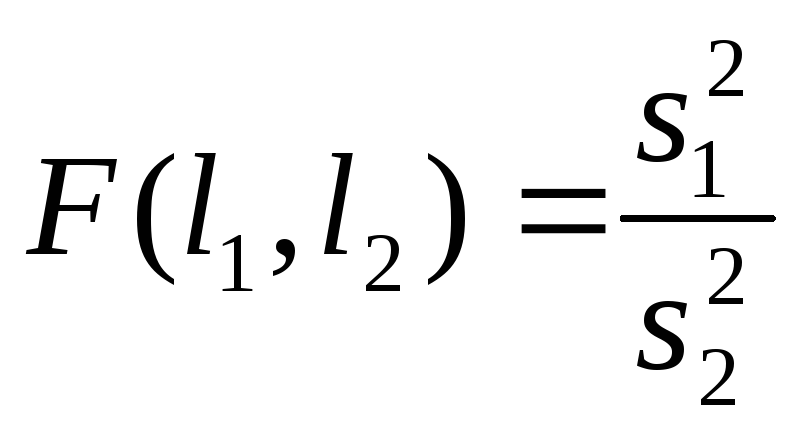или

; ()

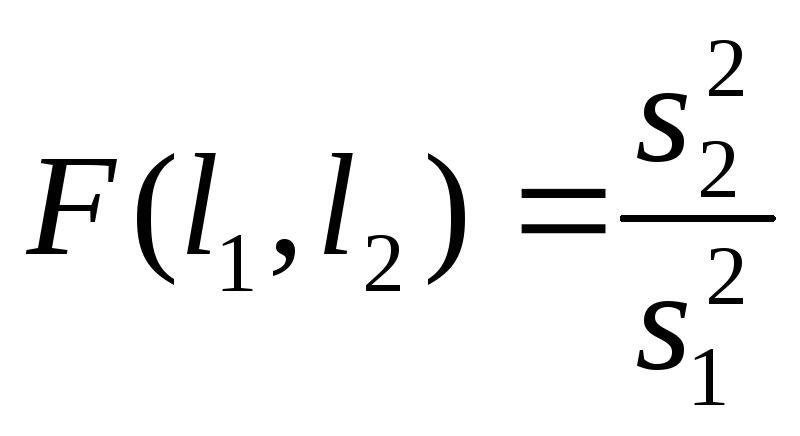Распределение этого отношения, называющееся F–распределением Фишера – Снедекора, зависит от двух параметров – чисел степеней свободы числителя и знаменателя и, где и – объемы выборок. Числаиуказываются в фигурных скобках рядом с вычисленным значением F:

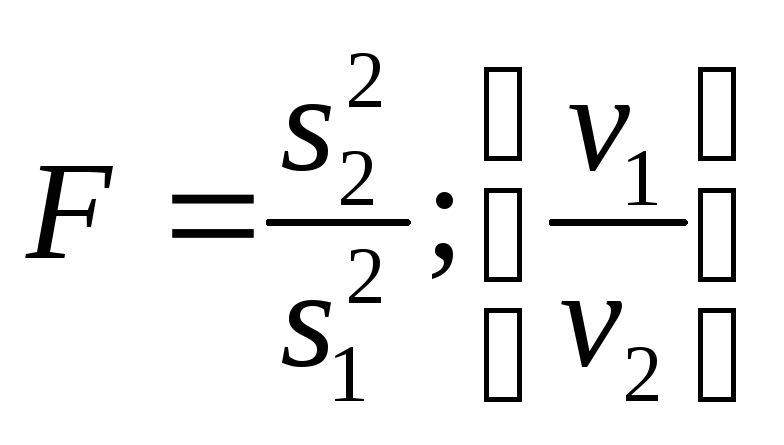
Критическая область строится в зависимости от вида альтернативной гипотезы:

1. Нулевая гипотеза . Альтернативная гипотеза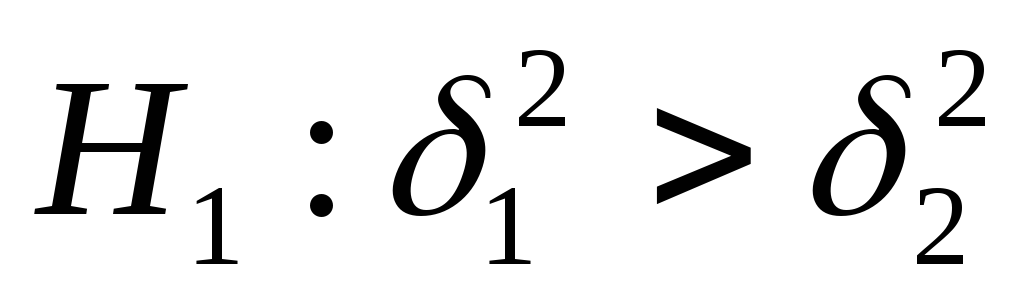, если ().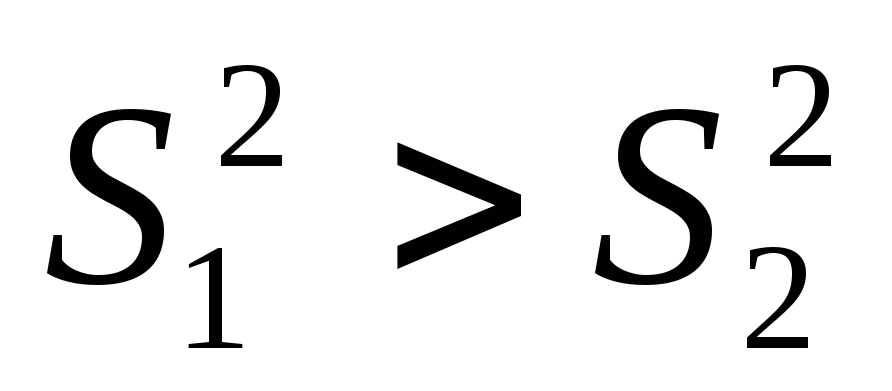

По заданному α и известным и по таблице распределения Фишера – Снедекора находим критическое значение. Проверка гипотезыH0 сводится к следующему правилу: если отношение выборочных дисперсий, гипотезаH0 отклоняется; если , гипотезаH0 не отклоняется.

2. Альтернативная гипотеза .

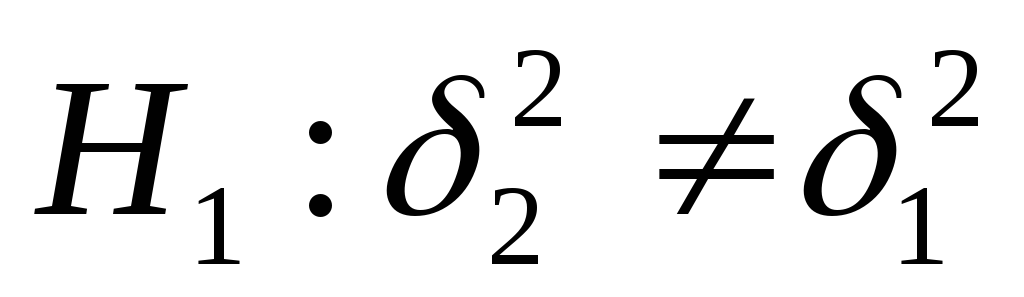В этом случае строим симметричную двустороннюю критическую область с критическими точками и, определяемыми из неравенств

;

Правая критическая точка находится непосредственно по таблице критических точек распределения Фишера – Снедекора для уровня значимости и степеней свободы и.Левых критических точек таблица не содержит, но, при выбранном симметричном способе построения критической области, достигается попадание критерияF в критическую область с вероятностью, равной уровню значимости .Так как из определения уровня значимости, то выбирая , мы одновременно достигаем и.Проверка гипотезы H0 производится по тому же правилу, что и в случае односторонней критической области, но табличные значения критерия ищутся для значения , вдвое меньшего, чем заданный уровень значимости: если отношение выборочных дисперсий, нулевая гипотезаH0 отклоняется, если гипотезаH0 не отклоняется.

§ 8. Непараметрические гипотезы. Критерии согласия Пирсона и Колмогорова.

Ранее рассматривались методы проверки гипотезы относительно отдельных параметров генерального распределения.

Особое место занимают гипотезы относительно согласованности выборочного распределения с теоретическим (генеральным) распределением.

Критерии согласия позволяют ответить на вопрос о том, являются ли различия между выборочным и теоретическим распределением столь незначительным, что они могут быть приписаны влиянию случайных факторов, или нет.

Пусть закон распределения генеральной совокупности неизвестен, но есть основания предполагать, что он имеет определенный вид.

В частности:

1) Если выполняются условия центральной предельной теоремы, есть основание ожидать, что генеральное распределение - нормальное;

2) Если выборочное среднее и выборочная дисперсия равны, то можно предполагать, что генеральная совокупность распределена по закону Пуассона и т.д.

Эти утверждения носят характер гипотез и должны быть подвергнуты статистической проверке.

Для проверки гипотезы : закон распределения имеет данный вид (нормальный, равномерный, показательный), используется специально подобранная случайная величина, котораяназывается критерием согласия.

Критерий согласия есть критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Имеется несколько критериев согласия:

- (хи-квадрат) Пирсона, критерий Колмогорова, Мизеса - Смирнова и др.