§ 7. Линейная регрессия. Выборочный коэффициент корреляции.

Так как объем выборки конечен, то о линии регрессии можно судить лишь по форме опытной линии регрессии. Задача о нахождении теоретической линии регрессии сводится к выравниванию статистических распределений, например, методом наименьших квадратов.

Прямые среднеквадратической линейной регрессии задаются уравнениями:

-прямая среднеквадратической регрессии Y на X,

-прямая среднеквадратической регрессии X на Y.

Здесь:

mx , my – средние значения,

σx, σy – среднеквадратические отклонения,

r – Коэффициент корреляции.

Глава 5. Основы дисперсионного анализа.

§ 1. Исходные понятия.

Объектами исследования дисперсионного анализа являются стохастические связи между откликом и факторами, когда последние носят не количественный, а качественный или именованный характер.

Будем обозначать факторы через A, B,С,…, а отклик при этом – через Х. Каждый из факторов имеет несколько уровней, или градаций. В зависимости от числа анализируемых факторов различают однофакторный, двухфакторный и т.д. дисперсионный анализ.

Если исследуется влияние одного фактора, то математическая модель однофакторного эксперимента выглядит как:

,

Где - значение признака Х, полученное в i-м эксперименте (i=1,..., n j), соответствующем j-му уровню фактора A , – общее среднее , - вклад в величину ,обусловленный действием фактора A (эффект фактора A на j-м уровне, - неслучайная величина),- случайная компонента, вызванная влиянием всех прочих факторов.

Если рассматривается влияние двух факторов (A и B), то математическая модель эксперимента имеет следующий вид:

,

Где -значение признака, полученное в k-м наблюдении на i-м уровне фактора A и на j-м уровне фактора B, – общее среднее, - эффект фактораA на i-м уровне, -эффект фактора B j -м уровне,-эффект, вызванный взаимодействием факторов,-случайная компонента.

§ 2. Групповое и общее среднее. Групповая, внутригрупповая, межгрупповая и общая дисперсии.

Пусть все значения признака X некоторой совокупности (генеральной или выборочной) разбиты на несколько групп. Рассмотрим каждую группу как отдельную совокупность соответствующего объема.

Групповое среднее – среднее арифметическое значений признака Х в данной группе.

Общее среднее – среднее арифметическое значений признака Х во всей совокупности.

Теорема.

Общее среднее равно среднему арифметическому групповых средних, взвешенному по объемам групп.

Групповая дисперсия- дисперсия значений признака X, принадлежащих группе, относительно группового среднего,

(суммирование идет по элементам k-й группы)

Внутригрупповая дисперсия – среднее арифметическое дисперсий, взвешенное по объемам групп,

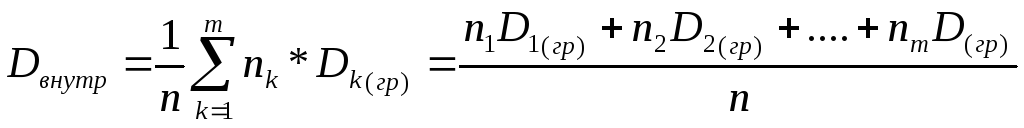
Межгрупповая дисперсия – дисперсия групповых средних относительно общего среднего,

Общая дисперсия – дисперсия значений признака X, принадлежащих всей совокупности, относительно общего среднего,

Теорема.

Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий.

Замечание.

Если групповые средние не различаются,, то=0 и внутригрупповая дисперсия совпадает с общей,(Dвнутр = Dобщ). Если же групповые средние различаются, то различаются и Dвнутр и Dобщ. Именно на сопоставление дисперсий и опирается дисперсионный анализ.