§6. Метод моментов для точечной оценки параметра распределения.

В рамках этого метода предложенного К.Пирсоном, в качестве точечных оценок теоретических моментов рассматриваемого распределения берутся эмпирические, выборочные моменты того же порядка.

Можно показать, что начальные и центральные выборочные моменты являются состоятельными оценками соответствующих теоретических моментов.

Пусть известен вид плотности распределения, зависящей от двух неизвестных параметров ;.

Требуется найти оценки этих параметров () по данным выборки (). Для нахождения оценок этих параметров составляют два уравнения, которые получаются следующим образом: приравниваем начальные моменты 1-ого порядка и центральные моменты 2-ого порядка.

=; или -теоретический начальный момент 1-ого порядка;

; или - теоретический центральный момент 2-ого порядка.

Эмпирические моменты:

1.Начальный момент:

2.Центральный момент

В общем случае, когда выборка это система случайных величин, то статистические моменты начальный и центральный тоже являются случайными величинами. ,

Глава 3.

Проверка статистических гипотез.

§1. Статистическая гипотеза. Основные понятия.

Задача проверки гипотезы в известном смысле напоминает задачу оценки параметров генеральной совокупности по данным выборки: высказывается некоторое утверждение и на основании данных выборки выносится суждение о справедливости этого утверждения.

Статистические гипотезы утверждают что-либо о статистически устойчивых событиях (события, которые могут протекать многократно при идентичных условиях).

1. Генеральная совокупность распределена по нормальному закону;

2. Дисперсии двух нормальных распределений равны;

3. дисперсия признака, распределенного в генеральной совокупности

0< D <2.

Определения.

• Если в гипотезе утверждается что-то о значении какого-то параметра, то гипотеза называется параметрической.

Если гипотеза предполагает что-то, количественно не измеряемое (например, «признак имеет нормальное распределение»), то гипотеза называется непараметрической.

• Основной (нулевой) гипотезой называют выдвинутую гипотезу.

• Альтернативной (конкурирующей) 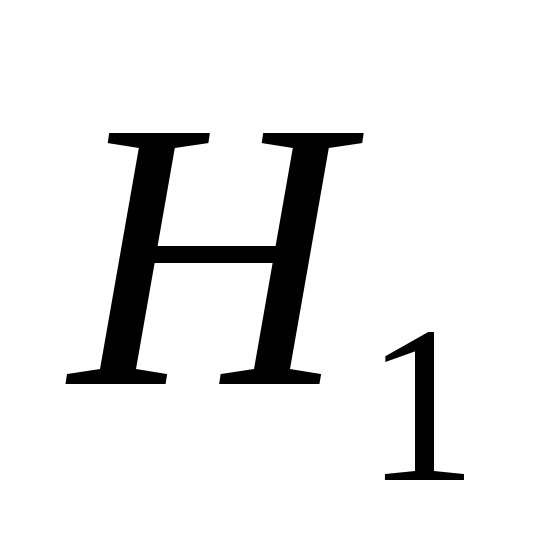называют гипотезу, которая противоречит выдвинутой.

• Гипотеза называется простой, если ответ на неё однозначен («признак распределения нормальный, дисперсия распределения равна 2»)

Если ответ неоднозначен, гипотеза называется сложной.

§2. Ошибки первого и второго рода.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому её необходимо проверить по эмпирическим данным (по выборки). Поскольку содержимое выборки случайно, то и высказывания, сделанные на основании исследования выборки, случайны, т.е. они могут быть и правильны, и неправильны.

В итоге проверки гипотезы может быть приняты неверные решения в двух случаях, т.е. могут быть допущены ошибки двух типов:

1. Ошибкой первого рода – называют ошибку, допускаемую в случае, когда отвергнута правильная основная гипотеза (отвергнута, хотя верна);

2. Ошибкой второго рода – называют ошибку, допускаемую в случае принятия неправильной, основной гипотезы (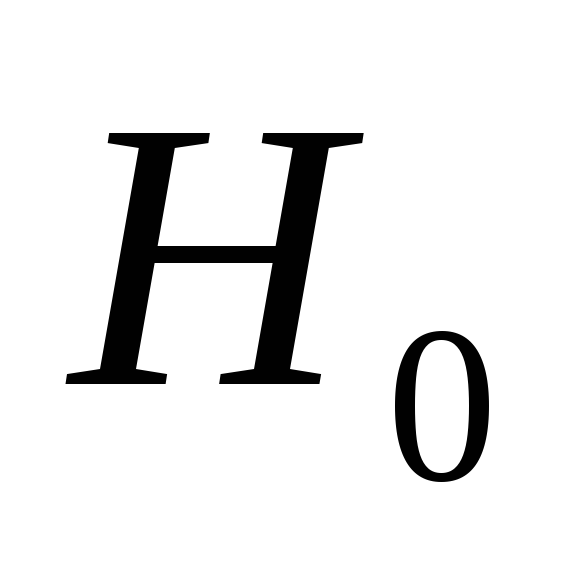принята, хотя она не верна);

Результат проверки основной гипотезы	Возможные состояния проверяемой гипотезы.
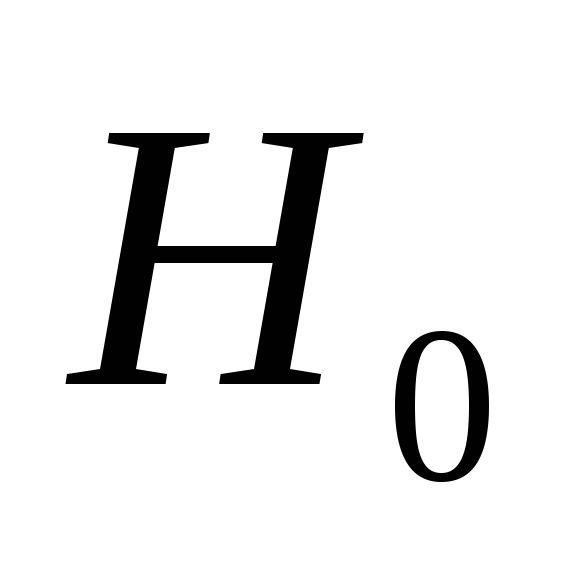
	Верна основная гипотеза	Верна альтернативная гипотеза
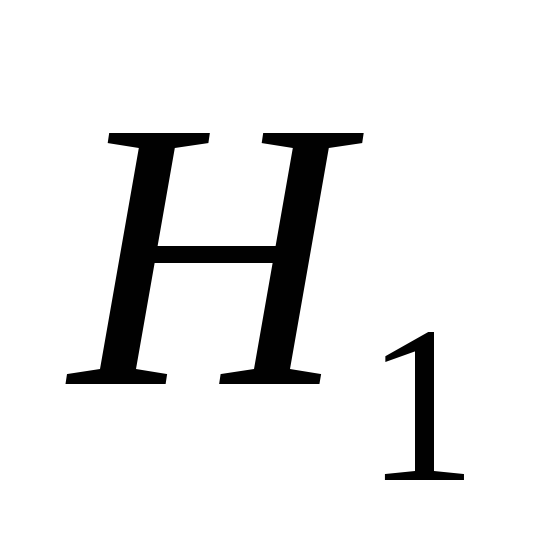
Гипотеза отклоняется	Ошибка 1-ого рода	Правильное решение
Гипотеза не отклоняется	Правильное решение	Ошибка 2-ого рода

Замечание

Не отрицательный результат статистической проверки гипотезы не означает, что высказанная нами гипотеза является наилучшей и единственной подходящей, просто она не противоречит имеющимся у нас выборочным данным, однако такими же свойствами могут обладать и другие гипотезы.

Принятие решения о правильности гипотезы или её ложности основано на статистических критериях.