§ 2. Элементы теории корреляции. Анализ парных связей.

Рассмотрим задачу о выборке показателя стохастической связи между двумя случайными величинами X и Y.

Пусть система имеет двумерный нормальный закон распределения.

Условная плотность распределения случайной величины Y при условии что , обозначается,

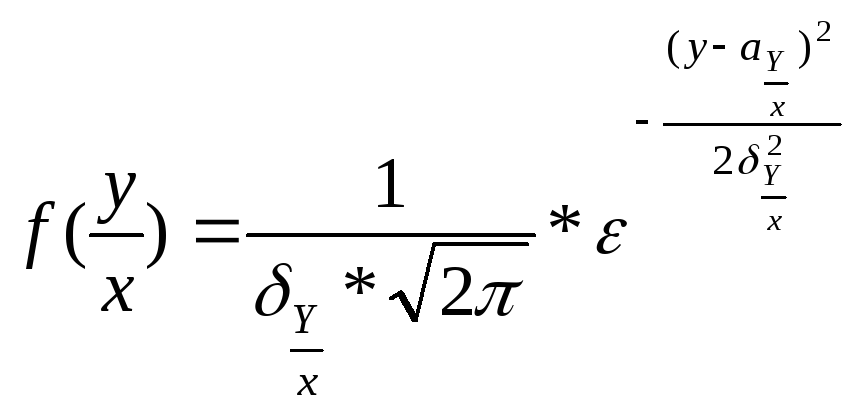
также является плотностью нормального распределения с параметрами:

- условное математическое ожидание;

- условная дисперсия;

При значение X=x, которые связаны с параметрами исходного распределения следующим образом:

;

.

В этом случае линия регрессии является прямой, а условная дисперсия не зависит от х.

Если закон распределения системы случайных величин (Х , Y) отличен от нормального, то характер изменения условного математического ожидания может быть и нелинейным.

Эта функция называется функцией регрессии.

Рассмотрим отклонение возможных значений случайной величины Y от её среднего значения .

(1) (2)

(1)- отклонение функции регрессии в точке х от математического ожидания .

(2)- отклонение возможного значения y, от значения функции регрессии в точке х.

Можно доказать, что рассеяние случайной величиныY относительно её математическое ожидание есть сумма двух слагаемых:

(1)

Из этого равенства следует, что связь между Y и X тем теснее, чем больше вклад в дисперсию вносит слагаемое.

В качестве такой характеристики принимается отношение ()называемое корреляционным отношением переменной:

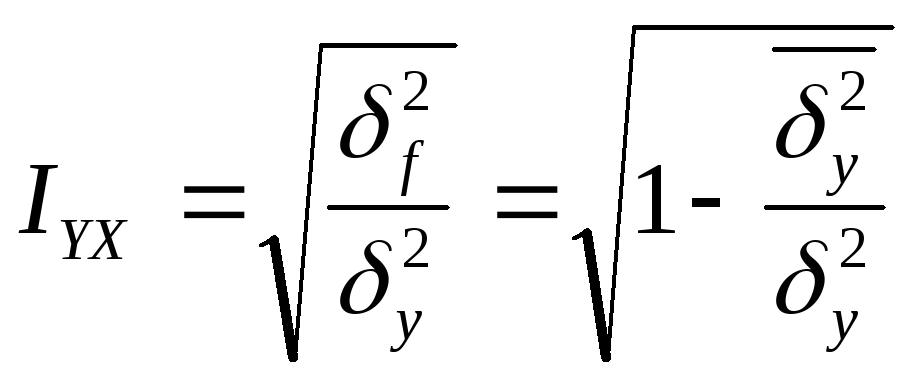(2)

Из равенства (2) следует, что .

Если , т.е, это означает, чтоX и Y связанны функциональной зависимостью.

Если , то линия регрессии - горизонтальная прямая , т.е условное математическое ожидание не меняется в зависимости от Х.

Аналогично определяется и корреляционное отношениепеременного Х по переменномуY.

Замечание.

Для выяснения степени тесноты связи необходимо рассматривать оба корреляционных отношения и.

Раннее мы рассмотрели, что связь между величинами можно измерить с помощью линейного коэффициента корреляции.

или

Для системы нормально распределенных случайных величин

справедливо следующее равенство:

(3)

В общем случае показатели исвязаны неравенствами:

(4)

При этом возможны следующие варианты:

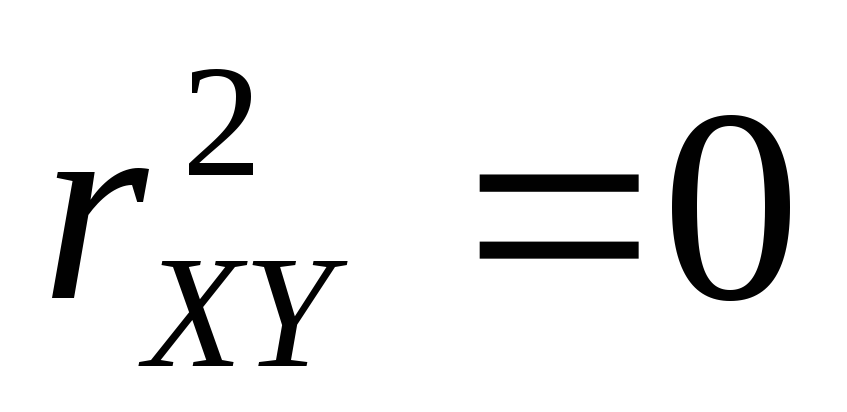• , если переменные Х и Y независимы, но обратное (в общем случае) неверно;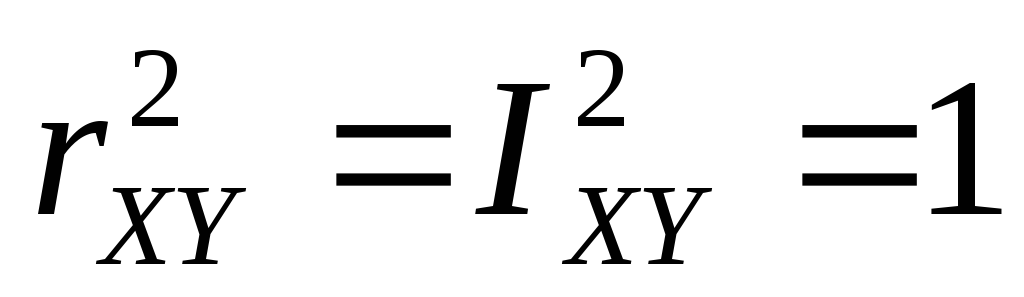

• ,тогда и только тогда, если у Х и Y имеется строгая линейная зависимость.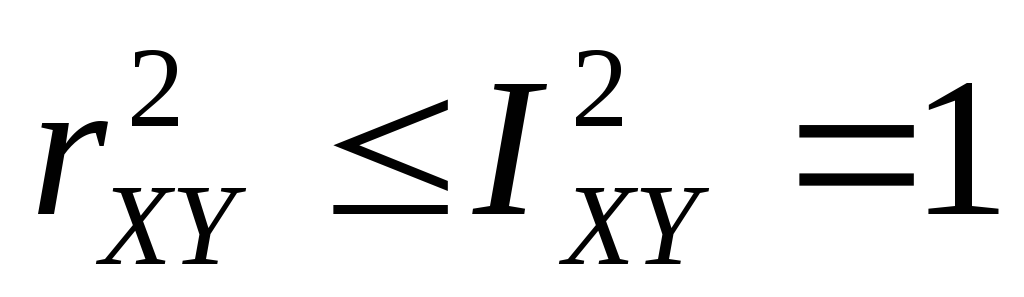

• , когда имеется строгая нелинейная функциональная зависимость Y от Х.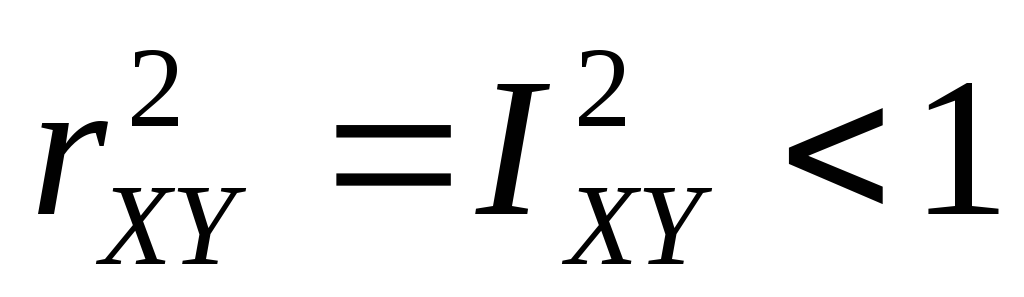

• , когда регрессия строго линейна, но нет функциональной зависимости.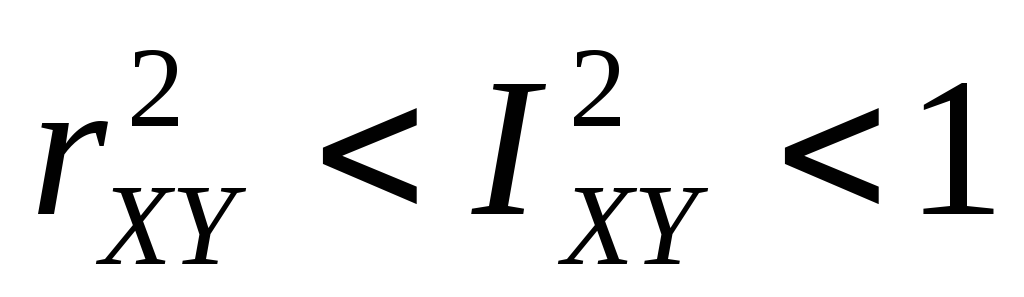

• указывает на то, что нет строгой функциональной зависимости, а некоторая нелинейная кривая регрессия приближает зависимость лучше, чем любая прямая линия.

В качестве показателя стохастической связи между двумя случайными количественными переменными Х и Y следует выбрать корреляционное отношение или, если закон распределения системы двухмерной случайной величины (Х ,Y) неизвестен.

Если же есть основание считать, что система (Х,Y) имеет нормальный закон распределения, то вместо корреляционного отношения следует использовать коэффициент корреляции.