§3. Несмещенные, состоятельные и эффективные оценки.

Для того чтобы статистической оценке можно было доверять, она должна обладать некоторыми свойствами.

Статистическая оценка *называется несмещенной, если её математическое ожидание M(*) равно оцениваемому параметру.

Несмещенность оценки означает отсутствие систематических ошибок в эксперименте (наблюдениях).

Статистическая оценка *называется состоятельной, если она сходится по вероятности к оцениваемому параметру, т.е для любого достаточно малого числа .

П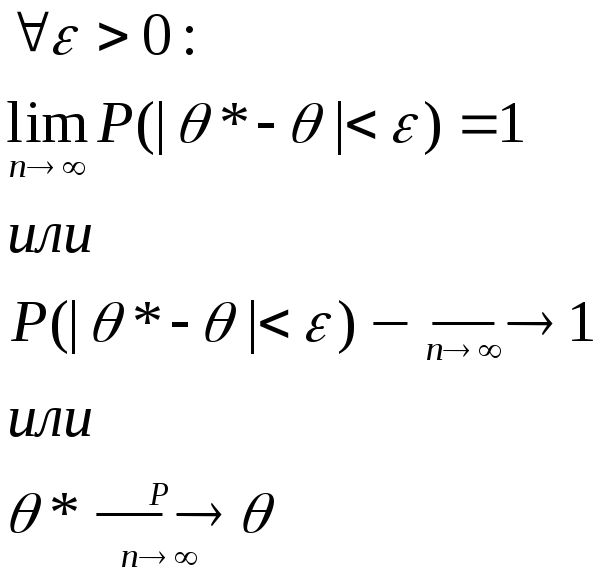редел вероятности того, что оценка* отличается от параметрапо абсолютной величине меньше чем напри ограниченном увеличение объема выборки равно 1.

Замечание.

Из неравенства Чебышева следует (закон больших чисел), что несмещенная оценка, дисперсия которой , при, является состоятельной.

Статистическая оценка * называется эффективной, если при данном объеме выборки из всех возможных оценок она имеет наименьшую дисперсию.

Замечание.

На практике не всегда удается добиться всех трех требований оценки. Из соображения практической удобности позволяют пользоваться не полностью адекватными оценками, но необходимо знать какими свойствами мы пренебрегаем.

§ 4. Точечная оценка генерального среднего по выборочной средней.

Пусть требуется изучить генеральную совокупность относительно количественного признака Х, имеем выборку и будем рассматривать эту выборку как реализованную систему случайных величин,т.е. выборку следует понимать в 2-ух смыслах:

1.Как систему ,n-независимых одинаково распределенных случайных величин, у каждой из которых закон распределения такой же, как у случайной величины Х (изучаемый признак).

2. Как конкретную выборку, где

- реализованная случайная величина

-реализованная случайная величина

-реализованная случайная величина

Выберем в качестве оценки генерального среднего M(X)=a, среднее арифметическое случайных величин ,

(для конкретной реализации выборки значение .)

Найдем математическое ожидание

М( т.к

Вывод:

Случайная величина – это несмещенная оценка математического ожидания генеральной совокупности.

По теореме Чебышева для любого ,

,

По этой теореме, используя предыдущее равенство можно записать, что:

, т.е., по определению, -состоятельная оценка

Если случайная величина распределения по нормальному закону

СВХ~N(a,), то оценка будетэффективной.

§ 5. Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии.

Пусть случайная величина Х- исследуемый признак.

- выборка.

-среднее значение квадратичных отклонений.

 

Покажем, что выборочная дисперсия () является смещенной оценкой генеральной дисперсии.

Найдем математическое ожидание дисперсии

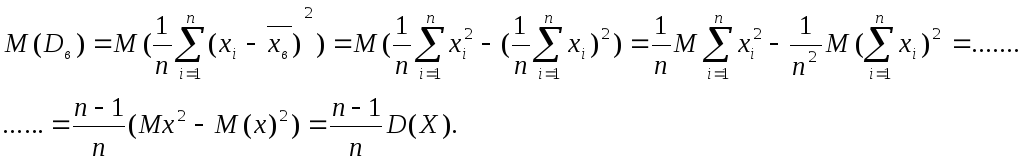
являетсясмещенной оценкой генеральной дисперсии.

Для получения несмещенной оценки достаточно перейти к исправленной выборочной дисперсии:

=;()

Очевидно, исправленная выборочная дисперсия является несмещенной оценкой генеральной дисперсии.

Покажем, что исправленная выборочная дисперсия является состоятельной оценкой генеральной дисперсии, т.е. для любого достаточно малого числа >0.

Т.е выборочная дисперсия является состоятельной оценкой генеральной дисперсии.

Замечание

Оценка =для генеральной совокупностине является эффективной, но для нормального распределения эта оценка является асимптотически эффективной, т.е. при () отношении дисперсии этой оценки к минимально возможной дисперсии оценки стремится к единице.