4. Метод размерностей

В случаях, когда отсутствуют уравнения, описывающие процесс, и составить их не представляется возможным, для определения вида критериев, из которых следует составить уравнение подобия, можно воспользоваться анализом размерностей. Предварительно, однако, необходимо определить все параметры, существенные для описания процесса. Это можно сделать на основе опыта или теоретических соображений.

Метод размерностей подразделяет физические величины на основные (первичные), которые характеризуют меру непосредственно (без связи с другими величинами), и производные, которые выражаются через основные величины в соответствии с физическими законами.

В системе СИ основным единицам присваиваются обозначения: длина L, масса M, времяT, температураΘ, сила токаI, сила света J, количество веществаN.

Выражение производной величины φчерез основные называется размерностью. Формула размерности производной величины, например при четырех основных единицах измерения L, M, T, Θ,имеет вид:

,

где a,b,c,d– действительные числа.

В соответствии с уравнением безразмерные числа имеют нулевую размерность, а основные величины – размерность, равную единице.

В основе метода кроме приведенного принципа лежит аксиома о том, что складываться и вычитаться могут только величины и комплексы величин, имеющие одинаковую размерность. Из этих положений вытекает, что если какая-либо физическая величина, например ∆p, определяется как функция других физических величин в виде∆p=f(V, ρ, η, l, d), то эта зависимость может быть представлена как:

,

где C– постоянная.

Если затем выразить размерность каждой производной величины через основные размерности, то можно найти величины показателей степени x, y, zи т.д. Таким образом:

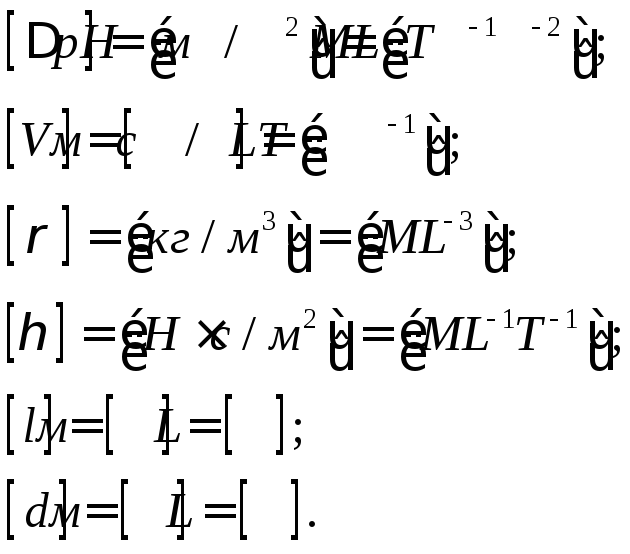
В соответствии с уравнением после подстановки размерностей получим:

.

Группируя затем однородные члены, найдем:

.

Если в обеих частях уравнения приравнять показатели степени при одинаковых основных единицах, то получится следующая система уравнений:

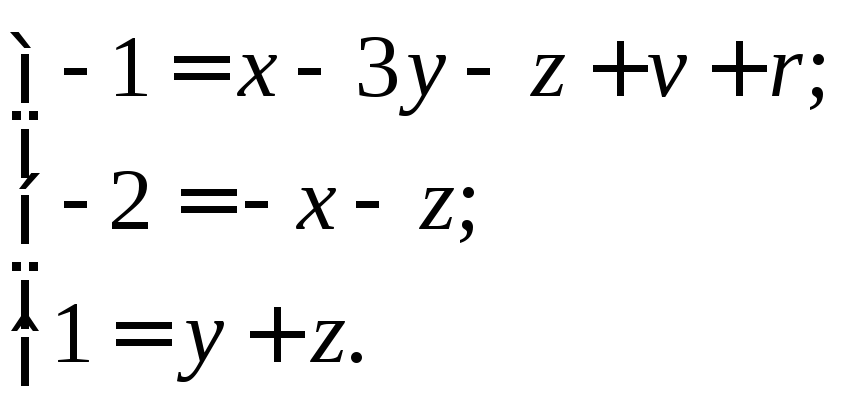
В этой системе из трех уравнений пять неизвестных. Следовательно, любые три из этих неизвестных можно выразить через два остальных, а именно x, yиrчерезzиv:

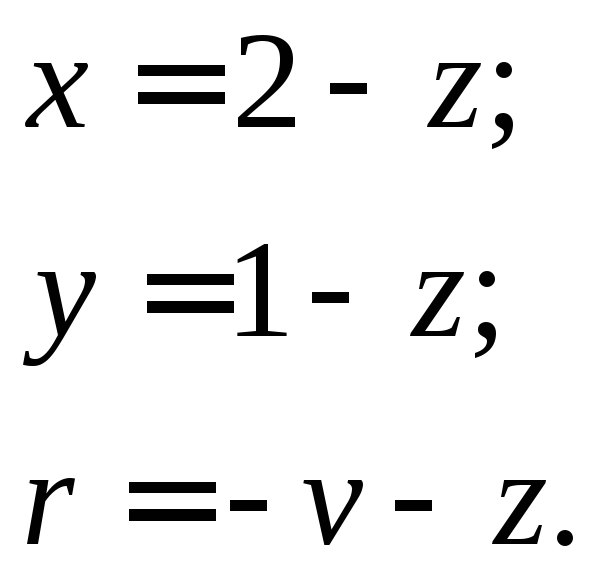
После подстановки показателей степени и в степенные функции получается:

,

затем:

.

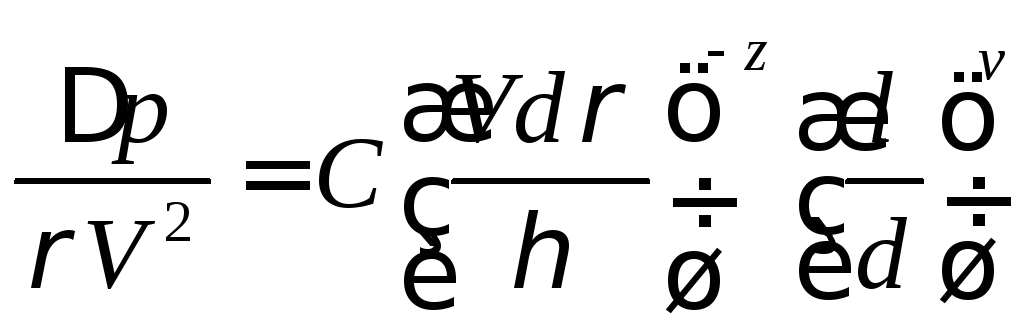Критериальное уравнение описывает течение жидкости в трубе. В это уравнение входят, как было показано выше, два критерия-комплекса и один критерий-симплекс. Теперь же с помощью анализа размерностей установлены виды этих критериев: это критерий Эйлера Eu=∆p/(ρV²), критерий РейнольдсаRe=Vdρ/ηи параметрический критерий геометрического подобия Г=l/d. Для того чтобы окончательно установить вид критериального уравнения, необходимо экспериментально определить значения постоянныхC,z и vв уравнении .

5. Экспериментальное определение констант критериального уравнения

При проведении опытов измеряют и определяют размерные величины, содержащиеся во всех критериях подобия. По результатам опытов вычисляют значения критериев. Затем составляют таблицы, в которые соответственно значениям критерия K₁вписывают значения определяющих критериевK₂, K₃и т.д. Этой операцией завершается подготовительный этап обработки опытов.

Для обобщения табличных данных в виде степенной зависимости:

используется логарифмическая система координат. Подбором показателей степени m, nи т.д. добиваются такого расположения опытных точек на графике, чтобы через них можно было провести прямую линию. Уравнение прямой линии дает искомую зависимость между критериями.

Покажем, как на практике определить константы критериального уравнения:

.

В логарифмических координатах lgK₂ – lgK₁это уравнение прямой линии:

.

Нанося опытные точки на график (Рис. 4), проводят через них прямую линию, наклон которой определяет значение постоянной m=tgβ.

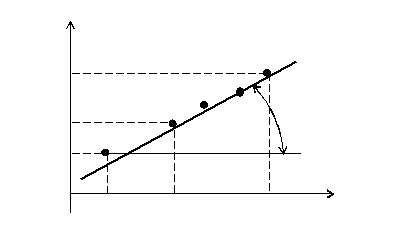
Рис. 4. Обработка опытных данных

Остается найти постоянную . Для любой точки прямой на графике. Поэтому значениеCнаходят по любой паре соответствующих значенийK₁и K₂, отсчитанных на прямой линии графика. Для надежности значения определяют по нескольким точкам прямой и в конечную формулу подставляют среднее значение:

.

При большем числе критериев определение констант уравнения несколько усложняется и проводится по методике, описанной в книге [33].

В логарифмических координатах не всегда удается расположить опытные точки вдоль прямой линии. Это случается, когда наблюдаемая зависимость не описывается степенным уравнением и надо искать функцию другого вида.