8.6 О выборе материала и рациональной формы поперечного

сечения сжатых стержней

Для стержней большой гибкости (λ≥ λ_пред) модуль продольной упругости Е является единственной механической характеристикой, определяющей сопротивление стержня потере устойчивости. Так как эта величина для всех сталей практически одинакова, то высокопрочные стали для таких стержней применять нецелесообразно.

Для стержней малой гибкости следует применять высокопрочные стали, так как прочность в этом случае будет зависеть от предела текучести σ_т.

С экономичной точки зрения наиболее рациональной будет такая форма поперечного сечения, у которой при определенной площади будет наибольший. Для удобства сравнения различных сечений вводится характеристика. Приведем значениядля некоторых сечений:

трубчатое сечение (α=0,95…0,8) 2,25…1,64

(α=0,7…0,8) 1,2 …1,00

уголок 0,5… 0,3

двутавр 0,41…0,27

швеллер 0,41…0,29

квадрат 0,289

круг 0,283

При проектировании сжатых стержней на устойчивость необходимо стремиться к тому, чтобы они были равноустойчивы во всех направлениях. К таким сечениям можно отнести трубчатые, квадратные или круглые сечения.

Пример. Подобрать двутавровое сечение стойки с одним защемленным концом и сжа-

   По сортаменту выбираем двутавр № 24, с площадью . Наименьший радиус инерции сечения=2,38 см. Соответствующая гибкость стойки.

Коэффициент по интерполяции между значениями его из таблицы дляиравен. Расчетное напряжением:МПа>160 МПа. Перегрузка составляет.

Рассмотрим двутавр № 27, а: ,; гибкость, так как коэффициент, то расчетное напряжениеМПа

Перегрузка составляет теперь, что допустимо.

8.7 Продольно - поперечный изгиб

Рассмотрим нагружение прямого шарнирно закреплённого стержня продольной силойFи системой поперечных сил. Такой вид нагружения принято называть продольно- поперчным изгибом. Обозначиму(z) прогиб балки в сеченииcабсциссойz. Воспользуемся дифференциальным уравнением упругой линии балки, в котором изгибающий момент можно рассматривать как сумму моментов поперечных сили момента продольной силыF·y. Полный прогибу складывается из прогибау_пот поперечных сил и дополнительного прогибау-у_п от осевой силыF . Полный прогибу больше суммы прогибов, возникающих при раздельном действии поперечных и продольных сил, так как при действии только силыFпрогиб равен нулю. Следовательно, в данном случае принцип независимости действия сил не применим.

( 8.5 ).

Разделим левую и правую части выражения (9.5) на EI:

(8.6)

Так как , то подставив это значение в (8.6), получим

,

или

(8.7).

Для упрощения решения предполагается, что дополнительный прогиб по длине балки изменяется по синусоиде, т.е.

(8.8).

Это допущение позволяет получить точные результаты при действии на балку поперечной нагрузки, направленной в одну сторону.

С учётом (8.8) выражение (8.7) примет вид

:.

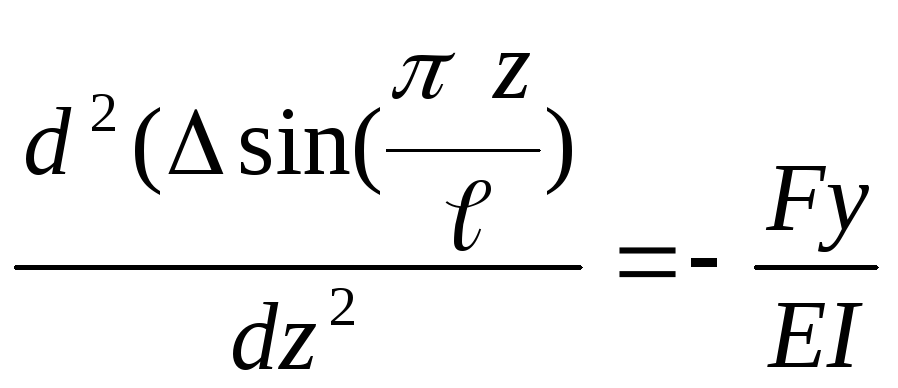После двухкратного дифференцирования этого уравнения получим

,

или .

Из этого равенства на ходим

.

Выражение =F_эсовпадает в формулой Эйлера, тогда

у=(8.9)

Необходимо отличать эйлерову силу F_эот критической силыF_кр, вычисляемой по формуле Эйлера для стержней большой гибкости (). Эйлерова силаF_э не зависит от гибкости стержня.

Из формулы (8.9), что отношение является критерием жесткости при продольно поперечном изгибе. Если→ 0, жёсткость балки велика и. При→ 1 жёсткость мала, балка очень гибкая и у→ ∞, т.е., прогибы многократно возрастают по сравнению с.

Формула (8.9) достаточно точная при F≤F_кр.

Расчёт на прочность при продольно – поперечном изгибе

Условие прочности при поперечном изгибе получено в предположении, что внутренние усилияизменяются пропорционально изменению внешних сил. Как установлено ранее, при продольно-поперечном изгибе эта зависимость нелинейная.

Предполагая, что моменты пропорциональны прогибам, можно записать

(8.10)

Будем считать, что при переходе к предельному состоянию внешние нагрузки возрастают пропорционально, тогда справедливы отношения

(8.11)

Здесь инагрузки, при которых в балке напряжения достигают предела текучести

(). Из (8.11) следует.

Наибольшие напряжения при поперечном изгибе с растяжением вычисляются по формуле

= .

При достижении предельного состояния они будут равны

=.

Разделив правую и левую часть этого уравнения на коэффициент запаса по текучести , получим

.

Так как , то условие прочности при продольно-поперечном изгибе примет вид

. (8.12)

Нелинейность в этом выражении определяется коэффициентом . За счёт этой нелинейности левая часть условия прочности будет несколько меньше.

77