
- •1. Основные понятия
- •1.2 Реальный объект и расчётная схема
- •1.3 Классификация внешних сил
- •1.4 Метод сечений
- •2. Геометрические характеристики поперечных сечений бруса
- •2.2 Геометрические характеристики простейших фигур
- •2.3 Зависимость между моментами инерции относительно
- •2.4 Главные оси и главные моменты инерции сечения
- •2.5 Зависимость между моментами инерции при повороте осей
- •2.6 Графический способ исследования моментов инерции. Круги Мора
- •2.7 Радиусы и эллипс инерции
- •3.7 Моменты инерции сложных сечений
- •3. Вычисление моментов инерции относительно центральных осей X,y
- •4.Определение главных центральных моментов инерции и положения
- •3. Центральное растяжение и сжатие
- •3.1 Напряжения при центральном растяжении, сжатии
- •3.2 Продольные и поперечные деформации при центральном
- •3.3 Испытание на растяжение. Основные механические характеристики
- •3. 4 Явление наклёпа
- •3.5 Расчёт на прочность при центральном растяжении, сжатии
- •3.6 Статически неопределимые задачи при центральном
- •3.7 Монтажные напряжения в статически неопределимых системах
- •4.Основы теории напряженного и деформированного состояния
- •4.1Основные понятия.
- •4.2 Закон парности касательных напряжений. Главные площадки, главные напряжения.
- •4.3 Виды напряженного состояния.
- •4.4 Линейное (одноосное) напряженное состояние.
- •4.5 Плоское (двухосное) напряженное состояние.
- •4.6 Графический метод исследования напряженного состояния в точке. Построение кругов Мора
- •4.6.1 Прямая задача
- •4.6.2 Обратная задача.
- •4.7 Напряжения на произвольной площадке при объемном напряженном состоянии
- •4.7.1 Круг Мора для объемного напряженного состояния.
- •4.9 Энергия изменения формы и объёма
- •5. Теории предельных напряженных состояний
- •6 Изгиб
- •6.1 Основные понятия об изгибе
- •6.2 Опорные устройства балок и их типы
- •6.3 Определение реакций
- •6.4 Внутренние усилия при изгибе
- •6.5 Дифференциальные зависимости при изгибе между q, q, m
- •6.6 Напряжения при изгибе
- •6.6.1 Нормальные напряжения при чистом изгибе
- •6.6.2 Напряжения при поперечном изгибе
- •6.7 Расчёт балок на прочность по допускаемым напряжениям
- •6.8 О рациональной форме поперечного сечения балки
- •6.9 Перемещения при изгибе.
- •6.10 Балки переменного сечения и балки равного сопротивления
- •7. Сдвиг, кручение
- •7.1 Сдвиг
- •7.1.1 Чистый сдвиг и его особенности
- •7.1.2 Зависимость между упругими характеристиками
- •7.2. Кручение
- •7.2.1 Основные понятия
- •7.2.2Связь между моментом внешних пар сил, передаваемой
- •7.2.3 Напряжения и деформации при кручении круглого вала.
- •7.2.4 Кручение брусьев некруглого поперечного сечения.
- •7.2.5Свободное кручение тонкостенных стержней открытого профиля
- •7.2.6 Свободное кручение составного открытого профиля
- •7.2.7 Кручение тонкостенного стержня с замкнутым профилем
- •8. Устойчивость сжатых стержней
- •8.1 Основные понятия
- •8.2Формула Эйлера для критической силы
- •8.3 Влияние условий закрепления стержня на величину
- •8.4 Критические напряжения. Пределы применимости формулы Эйлера
- •8.5 Расчеты на устойчивость с использованием коэффициента
- •8.6 О выборе материала и рациональной формы поперечного
- •8.7 Продольно - поперечный изгиб
4.6.2 Обратная задача.
Довольно часто приходится решать обратную задачу, т. е. по напряжениям на произвольных площадках sa,ta,sb,tbопределять величину и направление главных напряжений. Проще эта задача решается графически, т. е. с помощью круга Мора (рис. 4.10). Рассмотрим порядок его построения.
Прямоугольную систему координат s,tвыберем так, чтобы ось абсцисс была параллельна большему из нормальных напряжений (пустьsa>sb). На осиsотложим в выбранном масштабе отрезки ОКa, ОКb, численно равныеsaиsb. Из точек Кaи Кbпроведем перпендикуляры КaDa, КbDb, которые численно равны соответственноta и τβ (КaDa=ta,КbDb=τβ = - ta). На отрезкеDaDb, как на диаметре, построим круг с центром в точке С. Крайнюю правую точку пересечения круга с осьюsобозначим буквой А, крайнюю левую – буквой В. Касательные напряжения в этих точках равны нулю, следовательно, ОА=s1, ОВ=s2– главные напряжения (.в соответствии с прямой задачей).
t s2

Da
sb
s2
ta
sa 0 B Kb C Ka A s
a0 a0
s1 tb
s2
Db D¢a
sb
s1
sa
s1
Рис. 4.10
параллельна большему из нормальных напряжений (пусть sa>sb). На осиsотложим в выбранном масштабе отрезки ОКa, ОКb, численно равныеsaиsb. Из точек Кaи Кbпроведем перпендикуляры КaDa, КbDb, которые численно равны соответственноta и τβ (КaDa=ta,КbDb=τβ = - ta). На отрезкеDaDb, как на диаметре, построим круг с центром в точке С. Крайнюю правую точку пересечения круга с осьюsобозначим буквой А, крайнюю левую – буквой В. Касательные напряжения в этих точках равны нулю, следовательно, ОА=s1, ОВ=s2– главные напряжения (.в соответствии с прямой задачей).
Из рис.6.10 определим
радиус круга R и величину отрезка ОС
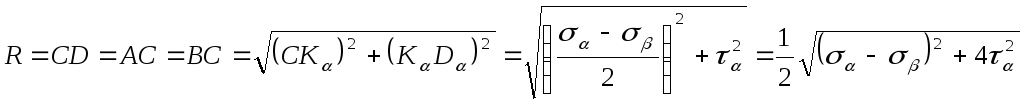 (4.12)
(4.12)
![]() (4.13)
(4.13)
Cучетом выражений (4.12) , (4.13) получим следующие формулы для главных напряжений
ОА=
σI
= ОС + R
=![]() +
+![]() (4.14)
(4.14)
ОВ
= σII= ОС – R =![]() -
-![]() (4.15)
(4.15)
Или
![]() (4.16)
(4.16)
Для определения направления главного напряжения s1проведем луч через крайнюю левую точку круга В и точкуDa¢, которая симметрична точкеDaотносительно осиs. Направление луча ВDa¢совпадает с направлениемs1, направлениеs2перпендикулярно ему. Уголa0определится из треугольника ВКaDa¢(рис. 6.10):
![]() (4.17)
(4.17)
Угол a0считается положительным, если его откладывают от осиsпротив часовой стрелки.
4.7 Напряжения на произвольной площадке при объемном напряженном состоянии
В элементарном параллелепипеде, по граням
которого действуют все три главных
напряжения, рассмотрим произвольную
площадкуa, нормаль
к которой составляет с координатными
осями 1,2,3 углыα1α2α3.(рис.
4. 11). На этой площадке будет действовать
полное напряжениерα,составляющее с нормальюnуголα. Определим
его проекции на нормаль к площадке -σα
и на саму площадку –τα.
элементарном параллелепипеде, по граням
которого действуют все три главных
напряжения, рассмотрим произвольную
площадкуa, нормаль
к которой составляет с координатными
осями 1,2,3 углыα1α2α3.(рис.
4. 11). На этой площадке будет действовать
полное напряжениерα,составляющее с нормальюnуголα. Определим
его проекции на нормаль к площадке -σα
и на саму площадку –τα.
Н
Рис.4.11![]() =
=![]() ,
,
где![]() -
напряжение на рассматриваемой площадке,
вызванное действием
-
напряжение на рассматриваемой площадке,
вызванное действием
![]() ,а
,а![]() ,
,![]() -
соответственно от напряжений
-
соответственно от напряжений![]() и
и![]() .Для
вычисления этих величин воспользуемся
формулой для линейного напряжённого
состояния:
.Для
вычисления этих величин воспользуемся
формулой для линейного напряжённого
состояния:![]() =
=![]()
![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .
.
С учетом этих значений нормальные напряжения на произвольной площадке определятся равенством
![]() (4.18
)
(4.18
)
Для вывода формулы
касательных напряжений ταследует рассмотреть его векторную
величину![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
Опуская выводы, которые следуют из уравнений равновесия рассматриваемой трёх- гранной пирамиды (рис. 3.11), запишем формулу в окончательном виде для вектора полного напряжения на площадке nα :
![]() .
.
С учётом этого выражения
![]() (4.19)
(4.19)
В качестве примера рассмотрим напряжения на площадке, равнонаклонённой ко всем главным площадкам. Такая площадка называется октаэдрической, а напряжения, действующие на этой площадке, называются октаэдрическими.
Так как для такой
площадки
![]() ,
а учитывая, что всегда
,
а учитывая, что всегда
![]() ,
то
,
то
![]() . Следовательно
. Следовательно
![]() (4.20)
(4.20)
 (4.21)
(4.21)
Так же, как и в случае плоского напряженного состояния, при объемном напряженном состоянии сумма нормальных напряжений по трем взаимно перпендикулярным площадкам, проходящим через рассматриваемую точку, есть величина постоянная.
