6.3. Способы вращения вокруг прямых частного положения

К способам вращения вокруг прямых частного положения относятся способы вращения вокруг проецирующих прямых и прямых уровня. Последний способ называется способом совмещения.

6.3.1. Способ вращения вокруг проецирующих прямых

Если некоторая точка А вращается вокруг проецирующей прямой i, то она будет перемещаться по окружности, плоскость которой перпендикулярна оси вращения, а, следовательно проецироваться эта окружность на плоскость проекций, перпендикулярную оси вращения, будет без искажения (рис.6.7, 6.8).

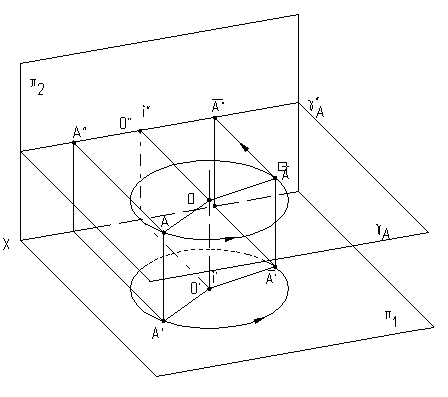
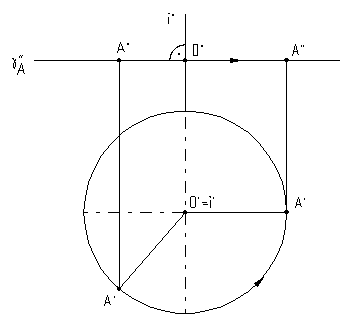
Рис.6.7 Рис.6.8

Для решения четырех основных задач на преобразование комплексного чертежа выбор осей вращения осуществляется из соображений упрощения процесса преобразования.

Покажем это на примерах решения четырех основных задач. 1-я и 2-я основные задачи решены на рис.6.9.

Чтобы преобразовать прямую l общего положения в прямую l уровня, достаточно выбрать на прямой две точки, например, А и В , а затем через одну из них провести ось вращения. Если, необходимо преобразовать прямую l (А, В) во фронтальную прямую , то достаточно через одну из выбранных на этой линии точек провести горизонтально проецирующую прямуюi. Приняв прямую i за ось вращения, повернуть горизонтальную проекцию прямой l до положения , параллельно оси проекций. При этом на фронтальной плоскости проекций расстояние между точкамиА^” и В^” будет проецироваться в истинную величину. 1-я основная задача решена.

Для решения второй основной задачи продолжим построения и повернем нашу прямую вокруг осиj, перпендикулярной к фронтальной плоскости проекций и проходящей через точку А, до положения, перпендикулярного горизонтальной плоскости проекций. Получим проецирующую прямую .Вторая основная задача решена. 3-я и 4-я основные задачи решены на рис.6.10.

Для преобразования плоскости (АВС) в проецирующую плоскость достаточно провести в плоскости линию уровня, например горизонталь h(h”,h’). Затем выбрать ось вращения i, перпендикулярную горизонтальной плоскости проекций и проходящую через точку С и повернуть горизонтальную проекцию треугольника АВС до положения, при котором горизонталь h’ станет фронтально проецирующей прямой. Тогда плоскость (АВС) станет фронтально проецирующей плоскостью. 3-я основная задача решена.

Для решения 4-й основной задачи достаточно продолжить построения и повернуть плоскость треугольника АВС вокруг проецирующей прямой j так, чтобы она расположилась параллельно горизонтальной плоскости, плоскости ₁. Четвертая задача на преобразование решена.

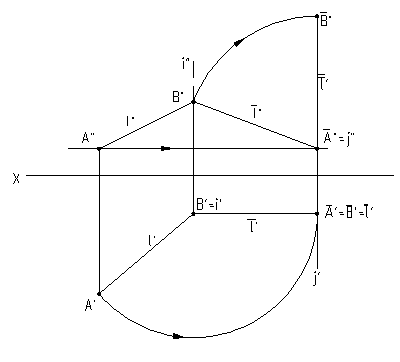
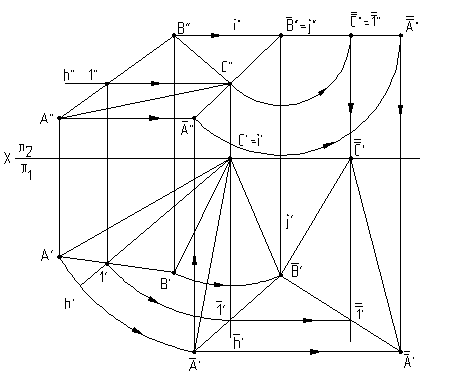
Рис.6.9 Рис.6.10

6.3.2. Способ вращения вокруг линии уровня

Способ вращения вокруг линий уровня используется в начертательной геометрии главным образом для определения натуральных величин плоских фигур.

На рис.6.11 приведен пример определения натуральной величины треугольника АВС. Это решение равносильно решению четвертой основной задачи на преобразование комплексного чертежа и состоит в следующем:

Во-первых, в плоскости заданного треугольника проводится линия уровня, например, фронталь, вокруг которой нужно повернуть заданную фигуру до положения, параллельного фронтальной плоскости проекций, или совместить эту фигуру с плоскостью , проходящей через выбранную линию уровня - фронталь f.

Во-вторых, поворот можно осуществить преобразовав заданную плоскую фигуру - треугольник АВС - в проецирующую плоскость, введя дополнительную плоскость проекций ₃, перпендикулярную фронтали f. Эта плоскость пересечет плоскость проекций ₂ по оси х₁. Проецируя треугольник АВС на эту плоскость, получим прямую А”’C”’B”’. Аналогично решению на рис.6.10, плоскость треугольника А”’C”’B”’можно преобразовать в плоскость уровня относительно фронтальной плоскости проекций ₂, повернув вокруг фронтали f  А”’C”’B”’ до положения `````````. При этом горизонтальная проекция треугольника``` совпадет с горизонтальной проекцией фронтали. ТреугольникАВС спроецируется на ₂ в истинную величину. Плоскость треугольника совместилась с ``.

Но задача может быть решена без введения дополнительной плоскости проекций ₃, так как натуральную величину радиуса вращения точки В можно определить с помощью способа прямоугольного треугольника. Его применение показано на исходном чертеже и дополнительного пояснения не требует.

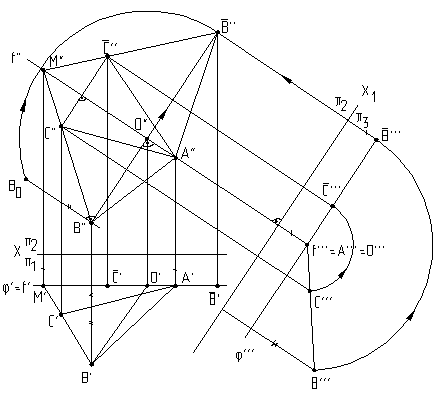
Рис.6.11

В случае задания плоскости ее следами, такую плоскость можно совместить с плоскостью проекций вращением вокруг соответствующего следа этой плоскости.

На рис.6.12 плоскость (h_0f_0), заданная следами, совмещена с горизонтальной плоскостью проекций. Для нахождения совмещенного положения плоскости на ее фронтальном следе выбрана произвольная точка N(N``,N`) и из нее опущен перпендикуляр NO(N``O``,N`O`) на горизонтальный след плоскости. Дальнейшее построение аналогично решению задачи на рис.6.11.

При совмещении плоскости общего положения с плоскостью проекций может быть найдено совмещенное положение любой фигуры, принадлежащей этой плоскости, например, точки А.

На рис.6.13 плоскость (h_0f_0) cовмещена с плоскостью ₂. Построения аналогичны и понятны из чертежа. При этом построении точка М(М``,M`) выбрана на горизонтальном следе плоскости, так как совмещение происходит путем вращения плоскости вокруг фронтального следа f_0 плоскости .

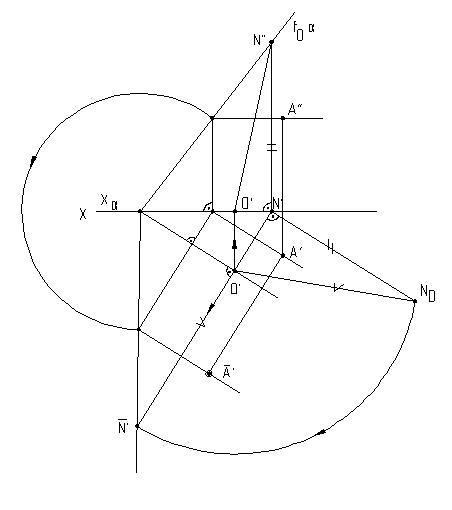
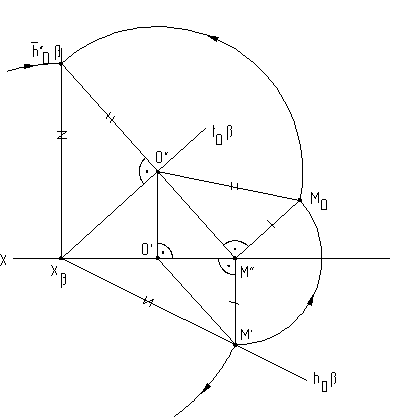
Рис. 6.12 Рис.6.13

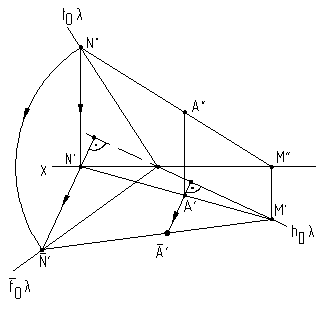
Рис. 5.14

На рис. 6.14 приведен пример совмещения тупоугольной плоскости  с горизонтальной плоскостью проекций. Совмещенное положение ` точки А , принадлежащей заданной плоскости, найдено с помощью вспомогательной прямой MN.

Литература:

Фролов С.А. Начертательная геометрия. М.: “Машиностроение”, 1983., гл.II, §§10,11,12.

Гордон В.О. и др. Курс начерт. геом. Изд. “Наука”, М.: Глава V, §§ 34, 37.

Локтев В.О. Краткий курс начерт.геом. М.: Гл.VII, §22.