6. Поле тяготения. Законы Кеплера. Космические скорости. Примеры решения задач.

Задача 1. Орбита искусственной планеты близка к круговой. Найти линейную скорость её движения и период Т её обращения вокруг Солнца, считая известным диаметр Солнца и его среднюю плотность . Среднее расстояние планеты от Солнца км.

Р ешение.

По второму закону Ньютона сила тяготения . По закону всемирного тяготения . Приравняв правые части, найдём ускорение

Масса Солнца . Тогда

С другой стороны центростремительное ускорение

Тогда

м/с.

суток.

Ответ: м/с; суток.

З адача 2. На экваторе некоторой планеты (плотность планеты г/см³) тела весят в два раза меньше, чем на полюсе. Определите период обращения планеты вокруг собственной оси.

Решение.

Вес на полюсе и на экваторе определяется как

Сила тяжести у поверхности планеты равна силе всемирного тяготения. Выражая массу планеты через плотность, находим ускорение свободного падения вблизи поверхности планеты

, ,

Линейную скорость точек поверхности планеты выразим через период обращения.

Тогда

ч.

Ответ: часа.

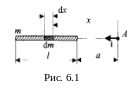
Задача 3. Имеется тонкий однородный стержень массой m и длиной l. Для точки, находящейся на одной прямой со стержнем на расстоянии a от его ближайшего конца, определите: 1) потенциал гравитационного поля стержня; 2) напряжённость его гравитационного поля.

Р ешение.

Разобъём стержень на элементарные участки длиной dx и массой dm. Тогда потенциал, создаваемый этим участком стержня определим как

Для определения потенциала для точки, надо проссумировать потенциалы, создаваемые каждым элементарным участком стержня, т.е. проинтегрировать

Тогда напряжённость гравитационного поля стержня

Ответ: ; .

Задача 4. Космическая ракета движется вокруг Земли по орбите, почти совпадающей с орбитой Луны. При включении тормозного устройства ракета быстро теряет скорость и начинает падать на Землю (см.рис. 6.2). Определите время падения ракеты на Землю. Сопротивлением воздуха атмосферы Земли и влиянием других тел пренебречь.

Р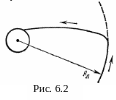 ешение.

Физическая система ракета – Земля. Происходит движение ракеты в поле тяготения Земли. Динамический метод приводит к сложному дифференциальному уравнению, а метод законов сохранения даёт лишь возможность найти скорость ракеты в любой точке траектории, но не искомое время падения. Возникает догадка (!) рассматривать движение ракеты как движение спутника планеты Земля по очень вытянутому эллипсу, длина большой оси которого равна радиусу орбиты Луны км, а эксцентриситет . Тогда можно использовать третий закон Кеплера

,

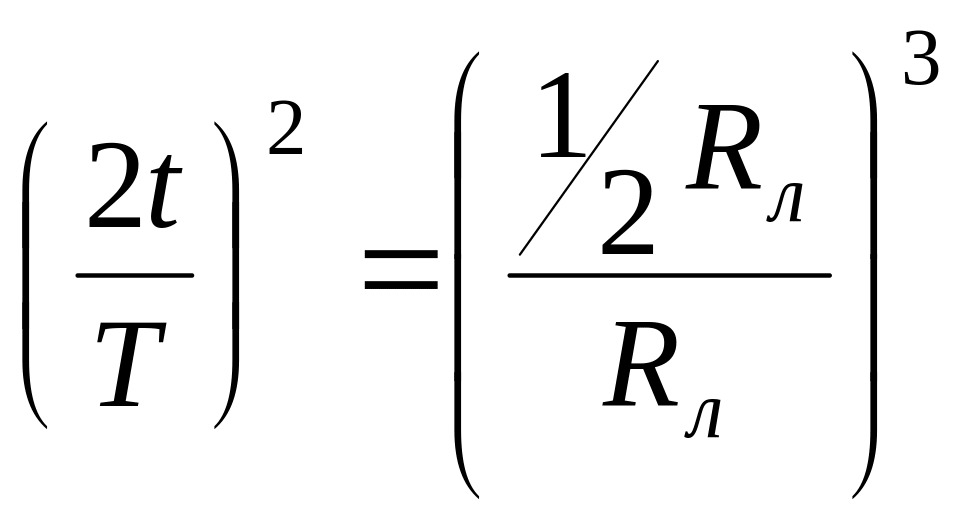где t - время падения, сут. – период обращения Луны вокруг Земли. После вычисления, находим:

суток.

Ответ: суток.

Задача 5. С полюса Земли запускают две ракеты, одну вертикально вверх, другую горизонтально. Начальные скорости обеих ракет равны , причём величина больше первой космической скорости и меньше второй. Какая из ракет удалится дальше от центра Земли и во сколько раз? Сопротивлением воздуха пренебречь.

Решение.

Рассмотрим вначале более простой случай, когда ракета запускается вертикально вверх. Поскольку единственная сила, действующая на ракету в свободном полёте, есть сила притяжения к Земле, направленная вертикально вниз, то ракета полетит по прямой, проходящей через центр Земли. Так как начальная скорость ракеты меньше второй космической, то ракета не может удалиться на бесконечность: на некотором расстоянии от центра Земли она становится и начнёт падать назад. Точку максимального удаления проще всего найти исходя из энергетических соображений. Действительно, так как полная механическая энергия системы ракета – Земля сохраняется, энергия вначале полёта ( ) равна энергии в точке остановки ( ). Отсюда сразу находим расстояние максимального удаления от центра Земли

Прежде чем вычислять величину максимального удаления ракеты при горизонтальном запуске, выясним вопрос о форме траектории. Поскольку начальная скорость ракеты превышает первую космическую, но меньше второй, ракета движется по эллипсу, у которого фокус находится в центре Земли, а начальная точка полёта является перигеем. Большая ось эллипса проходит через эту точку и центр Земли (см.рис. 6.3). Интересующая нас точка наибольшего удаления от центра Земли – апогей – лежит на противоположном конце большой оси, и скорость ракеты в этой точке, разумеется, отлична от нуля и направлена перпендикулярно большой оси эллипса.

Для нахождения величины опять можно воспользоваться законом сохранения энергии. Уже отсюда легко увидеть, что максимальное удаление ракеты в этом случае будет меньше, чем .

У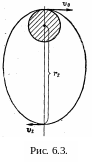 равнение имеет две неизвестные величины и и поэтому имеет бесчисленное множество решений. Что бы это могло означать? Перечитав ещё раз наши рассуждения, легко заметить, что в уравнение закона сохранения энергии не вошли никакие признаки, которые характеризовали бы точку как точку наибольшего удаления. Точно такое же уравнение мы получили бы и для любой другой точки траектории. Заметим, что в первом случае при вертикальном запуске ракеты точка максимального удаления была уже выделена в уравнении закона сохранения энергии, так как только в этой точке кинетическая энергия ракеты обращается в нуль. Подумаем, какое условие следует добавить к уравнению баланса энергии во втором случае, чтобы учесть особенности точки наибольшего удаления, отличающие её от всех остальных точек траектории. Мы уже заметили, что в этой точке скорость перпендикулярна к направлению на центр Земли. Этот факт позволяет нам в простом виде применить второй закон Кеплера о постоянстве секторной скорости, учитывая, что точно таким же свойством обладает и начальная точка траектории: по условию задачи начальная скорость перпендикулярна направлению на центр Земли. Во всех остальных точках это не так.

Добавляя к уравнению баланса энергии закон Кеплера для точек, в которых скорость перпендикулярна направлению на центр Земли: , получаем систему уравнений для нахождения , причём из наших рассуждений вытекает, что эта система должна иметь два решения, соответствующих перигею и апогею. 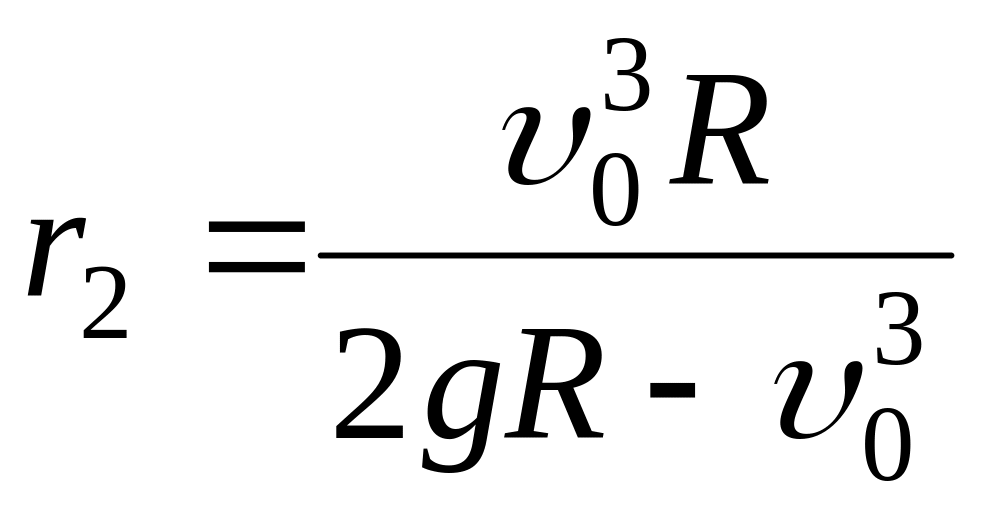Легко убедиться, что после подстановки уравнение баланса энергии превращается в квадратное уравнение относительно , корни которого равны R и ; сравнивая с , получаем:

.
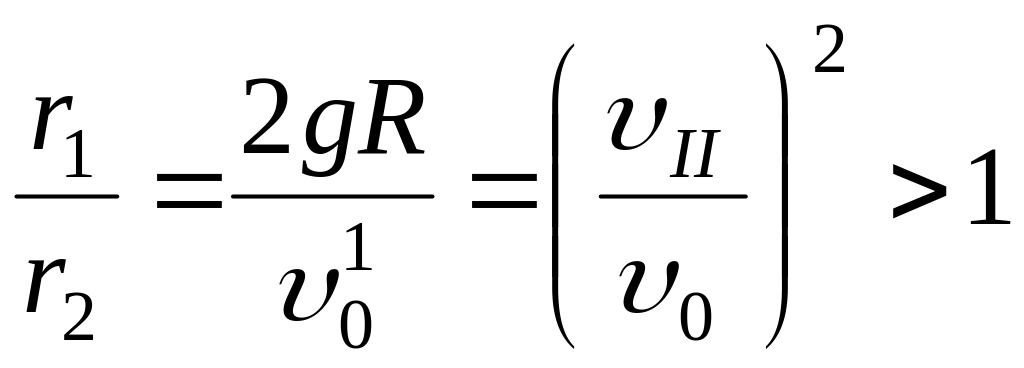