2.1.2. Графическое представление выборки.

Полигон, гистограммa, кривая

накопленных частот

Рисунки и графики – удобный и наглядный способ представления выборки. Выборку, извлеченную из дискретной генеральной совокупности, можно представить в виде полигона частот. На плоскости в прямоугольной системе координат строят точки с координатами (х_i, _i) и соединяют эти точки отрезками прямых. Полученная ломаная и называется полигоном частот. Полигон можно, конечно, построить и для сгруппированной выборки. Но такую выборку нагляднее всего представить в виде гистограммы. Гистограмма – это фигура, состоящая из прямоугольников. Основания прямоугольников – это интервалы, на которые разбита сгруппированная выборка. Высота i-го прямоугольника h_i определяется формулой

h_i = _i /h, i = 1, 2, 3,…, k.

Таким образом, высоты прямоугольников пропорциональны частотам интервалов, а сумма высот равна

.

Поэтому площадь гистограммы равна (1/h)*h = 1.

Гистограмма – это аналог графика функции плотности вероятности f(х) непрерывной случайной величины, площадь под графиком f(х) равна 1. Кривая накопленных частот (кумулятивная кривая) – это статистический аналог графика функции распределения F(x) непрерывной случайной величины. Кривая накопленных частот строится так: точки с координатами (х_i, _xi^нак) соединяют отрезками прямых. Кроме того, накопленные частоты для любого числа х < х₁ равны 0, накопленные частоты для любого числа х > х_k равны 1. Чтобы найти накопленную частоту для некоторого х₁ < х < х_k, нужно воспользоваться линейной интерполяцией. На рис. 2.1, 2.2, 2.3 показаны полигон частот для выборки 1, гистограмма и кумулятивная кривая для выборки 2 соответственно.

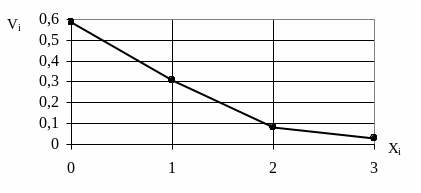
Рис. 2.1

h₁ = 0,1/0,3 = 0,33; h₂ = 0,22/0,3 = 0,73; h₃ = 0,34/0,3 = 1,13; h₄ = h₂ = =0,73; h₅ = h₁ = 0,33; h₆ = 0,02/0,3 = 0,067.

Покажем, как, используя линейную интерполяцию, найти относительную накопленную частоту _x^нак для числа х₁ < х < х_k .

Рис. 2.3

Пусть х принадлежит интервалу [х_i-1, х_i). Рассмотрим соответствующий участок кривой накопленных частот ( рис.2.4).

Рис. 2.4

Имеем: АС = h; АЕ = x - x_i-1; BC = ; DE = ;

∆ABC  ∆ADE.

Из подобия треугольников следует, что

, или .

Отсюда получаем

.

Например, в выборке 2 :

₄^нак = 0,66 + [(4 - 3,9)*(0,88 - 0,66)]/0,3 = 0,73.

Точно так же решается и обратная задача: по известной частоте _x^нак найти число х. Имеем

.

Например, для выборки 2 относительную накопленную частоту 0,5 имеет число

.

Действительно, если _x^нак = 0,5, то число х лежит внутри интервала [3,6; 3,9), так как _3,6^нак = 0,32 < 0,5, a _3,9^нак = 0,66 > 0,5.

2.2. Числовые характеристики выборки

2.2.1. Выборочное среднее, мода, медиана

Выборочное среднее – это среднее арифметическое вариант выборки. Если объем выборки равен n, то

,

где k - число различных вариант; n_i – частота варианты х_i, i = 1, 2, 3, ..., k.

Если выборка сгруппирована, то часто даже неизвестно, какие именно варианты попали в i-й интервал. Тогда частоту интервала n_i умножают на средину интервала. Конечно, при этом получается ошибка, так как варианты, попавшие в интервал, не обязаны все совпадать с числом (х_i + x_i-1)/2. Но эта ошибка не может быть слишком большой, особенно при достаточно больших n. Ведь в среднем половина вариант, попавших в интервал [x_i-1, х_i), будет меньше числа (х_i + x_i-1)/2, а половина – больше, поэтому ошибки будут иметь разные знаки и, таким образом, компенсируют друг друга. Легко видеть, что формула для выборочного среднего совпадает с формулой для вычисления математического ожидания дискретной случайной величины. Роль вероятностей играют относительные частоты _i.

Найдем выборочные средние для выборок, рассмотренных ранее.

1. Выборка 1.

.

Итак, в среднем из каждых 10 единиц товара 0,56 единицы дефектны.

2. Выборка 2.

Найдем сначала выборочное среднее непосредственно по выборке, а затем по сгруппированной выборке и сравним полученные числа.

В первом случае имеем:

= 1/50*( 3,7 + 3,85 + 3,7 + 3,78 + 3,6 + 4,45 + 4,2 + 3,87 + 3,33 + 3,76 + +3,75 + 4,03 + 3,75 +4.18+ 3,8 + 4,75 + 3,25 + 4,1 + 3,55 + 3,35 + 3,38 +3,3 + +4,15 + 3,95 + 3,5 + 3,88 + 3,71 + 3,15 + 4,15 + 3,8 + 4,22 + 3,75 + 3,58 + +3,55 + 4,08 + 4,03 + 3,24 + 4,05 + 3,56 + 3,05 + 3,58 + 3,98 + 3,88 + 3,78 + +4,05 + +3,4 + 3,8 + 3,06 + 4,38 + 4,2) = 3,78.

Средняя масса ребенка равна 3,78 кг.

Рассчитаем выборочное среднее по сгруппированной выборке.

= 3,15*0,1 + 3,45*0,22 + 3,75*0,34 + 4,05*0,22 + 4,35*0,1 + 4,65*0,02 = =3,77.

Расхождение равно 10 граммам. Но ведь и массы детей определялись с точностью до 10 граммов, так что мы не превзошли ошибки округления. Сам же подсчет оказался намного проще.

В теории вероятностей модой х_мо дискретной случайной величины называется такое её значение, которое имеет максимальную вероятность. Модой непрерывной случайной величины называется такое её значение, на котором достигается максимум функции плотности вероятности f(х). Закон распределения называется унимодальным, если мода единственна. Соответственно вводится понятие моды и в статистике. Модой (обозначают , читают “х с крышечкой”) называется варианта х_i с наибольшей частотой (относительной частотой). В выборке 1 мода = 0.

Если выборка сгруппирована, то сначала определяют модальный интервал, т.е. интервал с наибольшей частотой (относительной частотой). В качестве моды можно взять середину модального интервала. Эту оценку можно подправить с помощью простого дополнительного построения на гистограмме (рис. 2.5).

В выборке 2 модальный интервал – это интервал [3,6; 3,9). Тогда = =3,75. Так как высоты прямоугольников слева и справа от интервала [3,6; 3,9) одинаковы, подправлять значение не нужно.

В теории вероятностей медианой непрерывной случайной величины Х называется такое число х_ме, когда Р(Х < х_ме) = 0,5 = Р(Х > х_ме). Соответственно в статистике медианой (обозначают , читают “х с волной”) называют такое число , когда 50% вариант выборки меньше этого значения, а 50% больше его. Ясно, что для любой выборки можно подобрать бесконечно много медиан. Чтобы избежать неоднозначности, будем называть медианой число такое, когда = 0,5, где 0,5 – ордината точки с абсциссой на кривой накопленных частот.

Pиc 2.5

Чтобы найти медиану, нужно сначала найти медианный интервал [x_i-1; х_i), где _х^нак < 0,5; _xi^нак > 0,5, тогда  [x_i-1; x_i). Используя формулу, выведенную в пункте 2.1.2, получаем, что

.

В выборке 2 медианным интервалом является интервал [3,6; 3,9), так как _3,6^нак = 0,32; _3,9^нак = 0,66. Тогда

.