3.7. Индекс корреляции

Выборочный коэффициент корреляции r является мерой линейной связи между составляющими двумерной выборки. Если такая связь существует, но не является линейной, значение r не может служить ее мерой. Чтобы оценить, насколько хорошо соответствует экспериментальным данным некоторое квазилинейное уравнение регрессии у = f(x), используют индекс корреляции R_yx,, определяемый формулой

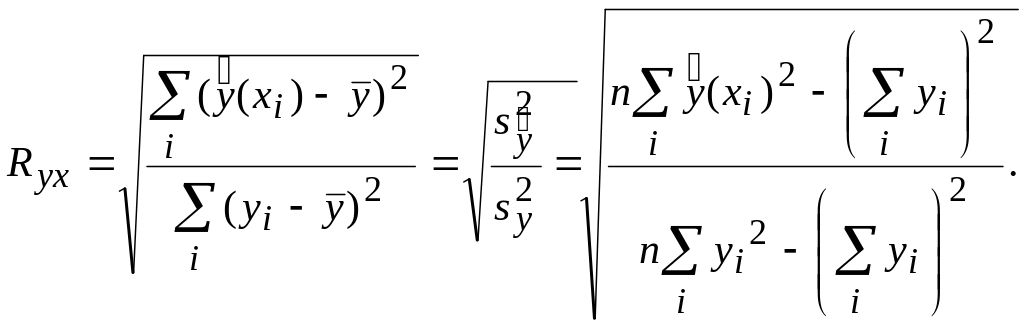
Если экспериментальные числа у_i совпадают с теоретическими значениями у(х_i) (точки (х_i, у_i) на диаграмме рассеяния лежат на кривой y = =f(x)), то R_yx = 1.

Так как всегда , то 0 ≤ R ≤ 1.

Чем ближе к 1 число R_yx , тем точнее уравнение регрессии соответствует экспериментальным данным, тем сильнее связь между значениями составляющих двумерной выборки.

Пример. Найдем индекс корреляции между объемом производства вишни и ценой вишни (пункт 3.5.5) при описании зависимости многочленом второго порядка. Расчетные данные:

n = 16; = 3722; = 232,625; = 13853284; = 918446; n = 471442,88;

R_yx=0,748, что несколько больше, чем модуль выборочного коэффициента корреляции r (r = -0,738). Мы получили подтверждение, что параболическое уравнение лучше соответствует опытным данным, чем линейное.

Индекс корреляции не позволяет определить, положительной или отрицательной является корреляция между величинами у и x (растут или убывают значения у с ростом x). Это можно сделать по виду диаграммы рассеяния и графика соответствующего уравнения регрессии.

В заключение отметим, что, построив уравнение регрессии x на у (x = =g(y)), можно рассчитать индекс корреляции R_xy ≠ R_yx, т.е. оценить, как x зависит от у.

3.8. Индекс фехнера и корреляционнное отношение

Здесь будут описаны два способа оценки степени связи между составляющими двумерной выборки без использования уравнения регрессии. Прежде всего, постараемся уточнить, что подразумевается под термином «связь». Ведь если нет уравнения у = f(x), связывающего аргумент x и зависимую переменную у, понятие «связь» становится расплывчатым. Будем говорить, что между составляющими двумерной выборки существует положительная корреляция (связь), если с ростом значений x значения y проявляют тенденцию к возрастанию. Соответственно говорят об отрицательной корреляции между x и у, если с ростом значений x значения у проявляют тенденцию к убыванию. Конечно, и формулировку «проявлять тенденцию к» нельзя назвать строгой. Но на интуитивном уровне она представляется понятной.

Г.Фехнер (1801 - 1887), немецкий психолог, предложил очень простой способ оценки степени такого рода связи. Для определения индекса Фехнера вычисляют средние , , а затем для каждой пары (x_i, у_i) определяют знаки отклонений х_i – , у_i – . Для каждой пары (x_i, y_i) возможны четыре сочетания знаков: + +; + —; — +; — —. Обозначим через V количество совпадений, через W – количество несовпадений знаков. Половину случаев х_i = или у_i = относят к V, половину – к W. Индекс Фехнера i определяется формулой i = (V-W)/(V+W).

Ясно, что -l ≤ i ≤ l и что при i > 0 имеем положительную корреляцию, при i < 0 – отрицательную, при i = 0 связь в указанном нами смысле отсутствует. Найдем индексы Фехнера для примеров из §3.1.

Пример с текстом. Пары знаков получаются такими:

(- -), (- -), (- -), (+ +), (- -), (- -) (+ +) (- -) (++), (++).

Отсюда V = 10, W = 0, i₁ = l.

Пример с монетами. Пары знаков следующие:

(- +), (- +), (- +), (- +), (- +), (+ -), (+ -) (+ +), (+ -), (+ -).

Значит V = 1, W = 9, i₂ = -0,8.

Пример с кубиками. Последовательность пар знаков:

(0 +), (+ -), (+ -), (- -), (- +), (+ -), (- -). (+ +), (+ -), (+ +).

Если просто не учитывать первую пару (x₁ = = 4), то V = 4, W = 5,

i₃ = -0,11. Если поделить единицу пополам, то V = 4,5 ; W = 5,5, i₃ = -0,1.

Корреляционное отношение как мера тесноты связи между составляющими двумерной выборки было предложено К. Пирсоном. Оно вычисляется по корреляционной таблице, а расчетная формула аналогична формуле для индекса корреляции. В дополнение к обозначениям §3.6 введем еще одно. Через обозначим т.н. частное среднее значений у для i-го значения х:

, i = 1,2, … , k.

По аналогии с индексом корреляции, корреляционное отношение η_yx вводится так:

Напомним, что

k – число интервалов группировки по составляющей x двумерной выборки;

x_i – середина i-го интервала группировки по составляющей x;

n_i – частота i-го интервала группировки по составляющей х, i = 1,2,..,k;

y_j – середина j-гo интервала группировки по составляющей y;

m - число интервалов группировки по составляющей у;

l_j – частота j-го интервала группировки по составляющей у, j =1,2,...,m;

n_ij – частоты прямоугольников группировки;

n – объем двумерной выборки.

Если все точки на диаграмме рассеяния сгруппированной выборки лежат на горизонтальной прямой, то все частные средние равны .

= , i = 1,2, … , k η_yx = 0.

Тогда говорят об отсутствии связи между значениями x и у. Если все точки на диаграмме рассеяния сгруппированной выборки лежат на некоторой прямой (кроме горизонтальной), то η_yx = 1. В остальных случаях 0 < η_yx < 1.

Величина η_yx зависит от группировки. Как правило, с ростом числа интервалов группировки по переменной x корреляционное отношение растет. По аналогии с числом η_yx можно рассчитать число η_xy ≠ η_yx, если считать x зависимой переменной, а у – независимой переменной.

Пример. На металлообрабатывающем заводе у 60 марок стали провели замеры предела текучести F(x, кг/мм²) и предела прочности σ_в (y, кг/мм²). В итоге получили 60 пар значений, представленных в табл. 3.6. Предполагается, что большие значения F обуславливают большие значения σ_в; марки стали с низким пределом текучести имеют и низкий предел прочности. Для обоснования гипотезы о высокой положительной корреляции между пределом прочности и пределом текучести сгруппируем выборку (табл. 3.7) и рассчитаем числовые характеристики.

Таблица 3.6

F	σв	F	σв	F	σв	F	σв
xi	yi	xi	yi	xi	yi	xi	yi
154	178	51	95	98	140	44	69
133	164	101	114	97	115	92	116
58	75	169	209	105	101	141	157
145	161	87	101	71	93	155	193
94	107	88	139	39	69	136	155
113	141	83	98	122	147	82	81
86	97	106	III	33	52	136	163
121	127	92	104	78	117	72	79
119	138	85	103	114	138	66	81
112	125	112	118	125	149	42	61
85	97	98	102	73	76	113	123
41	72	103	108	77	85	42	85
96	113	99	119	47	61	133	147
45	88	104	128	68	85	153	179
99	109	107	118	137	142	85	91

Внешний вид табл. 3.7 несколько отличается от вида табл. 3.5, иллюстрирующей двумерную группировку. Табл. 3.7 построена так, чтобы можно было легко вообразить диаграмму рассеяния, не строя ее саму.

Имеем:

n = 60; k = 7; m = 8; h_x = h_y = 20 (длины интервалов группировки).

(200*2 + 180*2 + 160*5 + 140*9 + 120*13 + 100*14 + 80*10 + 60*5) = 114,7;

Таблица 3.7

Предел прочности, кг/мм2	yj	Предел текучести [xi-1, xi], кг/мм2
		[30 –	[50 –	[70 –	[90 –	[110 –	[120 –	[150 –	mj
		50)	70)	90)	110)	130 )	150)	170)
		xi
		40	60	80	100	120	140	160
[190 – 210)	200							2	2
[170 – 190)	180							2	2
[150 – 170)	160						5		5
[130 – 150)	140			1	1	5	2		9
[110 – 130)	120			1	8	4			13
[90 – 110)	100		1	7	6				14
[70 – 90)	80	3	3	4					10
[50 – 70)	60	5							5
ni		8	4	13	15	9	7	4	60

(60*5 + 80*3) = 67,5; (80*4 + 100) = 105;

(160 + 120 + 100*7 + 80*4) = 100; = 113,3;

= 131,1; = 154,3; = 190;

= 8*(67,5 – 114,7)² + 4*(105 – 114,7)² + 13*(100 – 114,7)² + +15*(113,3–114,7)² + 9*(131,1–114,7)² +7*(154,3–114,7)² +4*(190 – 114,7)² = = 57115,8;

= 2*(200 – 114,7)² + 2*(180 – 114,7)² + 5*(160 – 114,7)² + +9*(140 – 114,7)² + 13*(120 – 114,7)² + 14*(100 – 114,7)² +10*(80 – 114,7)² + +5*(60 – 114,7)² = 69493,4;

η_yx = 0,82.

Для справки: коэффициент корреляции r = 0,92, предел прочности и предел текучести связаны сильной линейной зависимостью.