
- •Оглавление
- •Введение
- •1.Генеральная совокупность и выборка из генеральной совокупности
- •2. Выборка, ее представление и числовые характеристики
- •2.1. Представление выборки
- •2.1.1. Таблица частот и интервальная
- •2.1.2. Графическое представление выборки.
- •2.2. Числовые характеристики выборки
- •2.2.1. Выборочное среднее, мода, медиана
- •2.2.2. Квартили, декатили, персентили
- •2.2.4. О симметричных и несимметричных распределениях
- •2.2.5. Вычисление выборочного среднего и выборочной дисперсии для объединения двух выборок
- •1. , Тогда .
- •2.2.6. Общая, межгрупповая и внутригрупповая дисперсии
- •2.2.7. Кривая Лоренца и показатели концентрации
- •2.3. Задачи
- •3. Обработка результатов наблюдений по методу наименьших квадратов
- •3.1. Двумерные выборки
- •3.2. Графическое представление двумерных выборок — диаграммы рассеяния
- •3.3. Выборочный коэффициент корреляции — числовая характеристика двумерной выборки
- •3.4. Метод наименьших квадратов
- •3.5.6. Пример построения нелинейного уравнения регрессии
- •3.6. Расчет коэффициентов линейного уравнения регрессии по сгруппированным данным
- •3.7. Индекс корреляции
- •3.8. Индекс фехнера и корреляционнное отношение
- •3.9.Задачи
- •6. Проверка гипотезы о законе распределения генеральной совокупности по критерию пирсона (критерию 2)
- •6.1. Пример
- •6.2. Немного теории
- •1.3. Другие примеры
- •6.3.1. Проверка гипотезы о нормальном законе распределения
- •200 Отклонений диаметра вала от номинального размера (мкм)
- •6.3.2. Проверка гипотезы о равномерном законе распределения
- •6.3.3. Проверка гипотезы о биномиальном законе распределения
- •6.3.4. Проверка гипотезы о законе распределения Пуассона
- •6.3.5. Последний пример
- •6.4. Задачи
- •10. Результаты испытаний прочности партии стальной проволоки диаметром 1,4 мм:
6. Проверка гипотезы о законе распределения генеральной совокупности по критерию пирсона (критерию 2)
Те, что веруют слепо, - пути не найдут.
Тех, кто мыслит, - сомнения вечно гнетут.
Опасаюсь, что голос раздастся однажды:
«О, невежды! Дорога не там и не тут?»
О. Хайям (перевод Г. Плисецкого)
6.1. Пример
Рассмотрим такую ситуацию. 200 электронных ламп, выбранных наудачу из большой партии, испытывались на продолжительность работы. Результаты (в часах) таковы (табл. 6.1):
Таблица 6.1
[xi-1;xi) |
[0;300) |
[300;600) |
[600;900) |
[900;1200) |
[1200;1500) |
[1500;1800) |
ni |
53 |
41 |
30 |
22 |
16 |
12 |
[xi-1;xi) |
[1800;2100) |
[2100;2400) |
[2400;2700) |
[2700;3000) |
[3000;3300) |
|
ni |
9 |
7 |
5 |
3 |
2 |
|
Хотелось бы дать разумный ответ на такие вопросы: какую продолжительность работы следует ожидать, если взять наудачу лампу из этой же партии? Какова вероятность, что лампа проработает не менее 1000 часов? Какова вероятность того, что лампа проработает менее 200 часов? Ответить на эти вопросы легко, если известен закон распределения случайной величины Х – времени работы лампы. Но его-то мы не знаем. Мы располагаем только выборкой (правда, достаточно большой, n = 200) из генеральной совокупности X. Попробуем, пользуясь этой выборкой, подобрать подходящий закон распределения.
Построим прежде всего гистограмму (рис. 6.1).
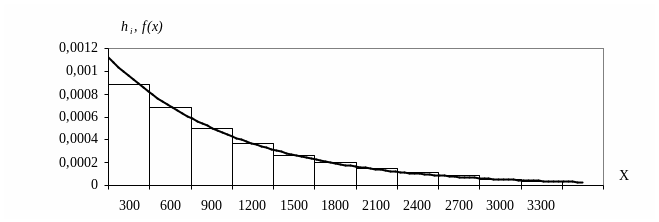 Рис.
6.1
Рис.
6.1
Высоты прямоугольников таковы:
![]() ;
;
![]() ;
;
![]() ;
h4
= 0,00037; h5
= 0,00027; h6
= 0,0002;
h7
= 0,00015; h8
= 0,00012; h9
= 0,00008; h10
= 0,00005; h11
= 0,00003.
;
h4
= 0,00037; h5
= 0,00027; h6
= 0,0002;
h7
= 0,00015; h8
= 0,00012; h9
= 0,00008; h10
= 0,00005; h11
= 0,00003.
Гистограмма – аналог графика функции плотности вероятности. В нашем случае гистограмма очень похожа на график функции плотности показательного закона. Мы вправе предположить, что большая выборка хорошо представляет генеральную совокупность и что если гистограмма похожа на график экспоненты, то это означает, что выборка извлечена из генеральной совокупности, распределенной по показательному закону с функцией плотности вероятности
f(x) = e-x.
Однако показательный закон зависит от одного параметра – числа . Чтобы полностью описать закон, нужно знать, чему равно . Подберем значение по выборке, причем поступим самым бесхитростным способом. Как известно, математическое ожидание случайной величины, имеющей показательное распределение, М(Х) = 1/. Если наша выборка хорошо представляет генеральную совокупность, мы вправе полагать, что значение выборочного среднего не слишком отличается от М(Х). Поэтому найдем и положим =1/ .
![]()
+19509
+22507![]() .
.
Тогда = 1/ 0,00115, f(x) = 0,00115e -0,00115x ,x 0.
Вычислим значения f(х) на границах интервалов (табл. 1.2) и построим график функции плотности вероятности прямо на гистограмме
(см. рис. 6.1).
Таблица 6.2
xi |
0 |
300 |
600 |
900 |
1200 |
1500 |
f(xi) |
0,00115 |
0,00081 |
0,00058 |
0,00041 |
0,00029 |
0,0002 |
xi |
1800 |
2100 |
2400 |
2700 |
3000 |
3300 |
f(хi) |
0,000115 |
0,0001 |
0,00007 |
0,00005 |
0,000037 |
0,000026 |
Не следует увлекаться слишком большим количеством значащих цифр, ведь все наши данные достаточно приближенные.
Кривая функции плотности вероятности f(х) очень «ладно» легла на гистограмму. Такое хорошее совпадение гистограммы и графика f(х) прибавляет уверенности в том, что закон распределения генеральной совокупности Х выбран достаточно точно.
Попробуем теперь оценить числом расхождение между экспериментальными данными и тем, что должно быть «по теории».
Мы можем вычислить теоретическую вероятность рi попадания случайной величины X, распределенной по показательному закону с функцией плотности f(x) = 0,00115е-0,00115x, x 0 в интервал [xi-1, xi).
р(хi-1
< X
< xi)
=
![]() .
.
Зная вероятность pi, можно вычислить математическое ожидание числа попаданий случайной величины Х в интервал [xi-1, xi) в результате n независимых испытаний, оно равно nрi. Теперь можно найти разность
ni - nрi между числом вариант выборки, попавших в интервал [хi-1, хi), и ожидаемым числом попаданий. Чтобы оценить суммарное расхождение между теоретическими и опытными данными, нужно сложить все полученные разности. Чтобы положительные и отрицательные разности не уничтожили друг друга, возведем их в квадрат. Кроме того, важно не абсолютное значение ni - nрi, а относительное (ni,- npi)/npi. Действительно, если ni = 0, nрi = 1, это совсем не одно и то же, что в случае, когда ni = 10, nрi = 11. Относительное отклонение в первом случае равно 1, а во втором
только 1/11.
Итак, вычислим прежде всего вероятности рi.
р1 = P(0 < X < 300) = e-*0 - e-*300 = e 0 - e –0,345 = 1- 0,708 = 0,2918;
p2 = P(300 < X < 600) = e-*300 - e-*600 = 0,7082 – 0,5016 = 0,2066;
р3 = P(600 < X < 900) = e-*600 - e -*900 = 0,1464;
р4 = 0,1036; р5 = 0,0734; р6 = 0,052; р7 = 0,0368; р8 = 0,0261;
р9 = 0,0185; р10 = 0,0131; р11 = 0,0092.
Дальнейшие вычисления приведены в табл. 6.3.
Таблица 6.3
[xi-1; xi) |
pi |
npi |
ni |
ni - npi |
|
[0;300) |
0,2918 |
58,36 |
53 |
-5,36 |
0,490 |
[300;600) |
0,2066 |
41,32 |
41 |
-0,32 |
0,002 |
[600;900) |
0,1464 |
29,28 |
30 |
0,72 |
0,018 |
[900;1200) |
0,1036 |
20,72 |
22 |
1,28 |
0,079 |
[1200;1500) |
0,0734 |
14,68 |
16 |
1,32 |
0,119 |
[1500;1800) |
0,0520 |
10,40 |
12 |
1,60 |
0,246 |
[1800;2100) |
0,0368 |
7,36 |
9 |
1,64 |
0,365 |
[2100;2400) |
0,0261 |
5,22 |
7 |
1,78 |
0,607 |
[2400;2700) |
0,0185 |
3,70 |
5 |
1,30 |
0,457 |
[2700;3000) |
0,0131 |
2,62 |
3 |
0,38 |
0,056 |
[3000;3300) |
0,0092 |
1,84 |
2 |
0,16 |
0,014 |
– |
pi = 0,9775 |
npi = 195,5 |
ni = 200 |
– |
2 = 2,45 |
Сумма вероятностей pi равна 0,9775. Это значит, что интервал [0; 3300) охватывает практически все возможные значения выбранного нами теоретического закона. Сумма чисел последнего столбца традиционно обозначается буквой 2 (читается «хи - квадрат»). В нашем случае
![]() .
.
Много это или мало?
