9 .. Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для линейных пм

С целью упрощения реальную систему электропривода приводят к одной оси, чаще всего к валу электродвигателя со скоростью ω. При этом механические звенья электропривода принимаются абсолютно жесткими.

В результате приведения реальная многомассовая система (рис. 1.14 а) приводится к одномассовой системе (рис. 1.14 б), имеющей суммарный момент инерции J, статический момент Мс, угловую скорость ω и угол поворота вала φ.

При принятом допущении на основании закона сохранения энергии имеем равенство:

Мс ω = М_М ω_Н,

из которого находим выражение для статического Мс (приведенного ) момента

(1.79)

Следовательно, статический момент на валу электродвигателя при отсутствии потерь в передаче численно равен моменту сопротивления М_М на валу исполнительного механизма ИМ, деленному на передаточное число j. В этом и состоит сущность приведения моментов сопротивления к валу электродвигателя.

П ри поступательном движении исполнительного механизма (рис. 1.15 а) и допущении об идеальности передачи с соблюдением закона сохранения энергии имеет равенство

Мс ω = Fс

где – линейная скорость механизма,

Fc – сила сопротивления в установившемся движении,

Мс – эквивалентный статический момент на валу двигателя одномассовой системы (рис. 1.15 б).

,

где ρ – радиус приведения поступательного движения к вращательному.

Для линейных передаточных механизмов (j=const, ρ=const) рассмотрим приведения моментов инерции и масс к валу электродвигателя. При вращательном движении исполнительного механизма (см. рис. 1.14 а) и идеальном ПМ кинетическая энергия неприведенной системы должна равняться кинетической энергии приведенной системы (см. рис. 1.14 б), т.е.

,

откуда находим суммарный момент инерции приведенной системы:

где

– приведенный к валу электродвигателя момент инерции механизма.

Для поступательного движения исполнительного механизма (см. рис. 1.15а) записываем равенство кинетических энергий приведенной и неприведенной систем:

из которого получаем

где

– приведенный к валу электродвигателя момент инерции поступательно движущейся массы m,

– момент инерции ротора электродвигателя,

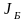– момент инерции барабана, соединенного с ротором ЭД.

Следовательно, приведенный к валу электродвигателя момент инерции поступательно движущейся массы равен произведению этой массы на квадрат радиуса инерции.

10.Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для нелинейных пм

н а примере кривошипно-шатунного механизма (рис. 1.16). Пренебрегаем потерями в кривошипно-шатунном механизме и массой его элементов.

По закону сохранения энергии

F_В = F_A ,

откуда

F_A= F_В ,

Где =ω_К·r ,

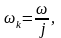
– линейная скорость точки А,

ω_К – угловая скорость кривошипа АО,

r – радиус кривошипа,

ω – угловая скорость ротора электродвигателя,

j – передаточное число ПМ.

Поскольку при ω_К=const скорость ползуна В изменяется как по величине, так и по направлению при изменении угла поворота φ кривошипа ОА, то и сила в точке А будет функцией угла, т.е. F_A=F(φ).

Момент силы F_A относительно точки О

M_O(F_A)= F_A·r= F_В·r· =М_М

Обозначим m_B как массу ползуна и перемещаемого им изделия. Тогда кинетическая энергия движущейся массы m_B будет равна

W_B=m_B

Приведем эту кинетическую энергию в точку А с фиктивной массой m_A, имеющей линейную скорость :

m_B = m_A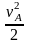 m_A=m_B

Момент инерции точечной массы m_A относительно оси О по определению равен

J₀(m_A)=J_M= m_Ar­­­²=m_Br­­­²

Приведение этого момента инерции к валу электродвигателя выполняется в соответствии с правилом (1.82):

Для аналитического определения Мс и необходимо найти отношение . С этой целью воспользуемся следствием одной из теорем теоретической механики: при плоском движении проекции скоростей двух точек на прямую, проходящую через эти точки, равны, т.е.

_(АВ) = _(АВ) cosβ= sin(φ+β),

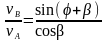
или

Для треугольника ОАВ (рис. 1.16) по теореме синусов имеем

откуда

Теперь можно записать аналитическое выражение для приведенного к валу электродвигателя момента сопротивления

которые являются функцией угла поворота φ кривошипа ОА.

Расчеты динамики электропривода при переменном моменте инерции весьма сложные. Поэтому в расчетах обычно учитывают фактическую зависимость Мс=F(φ), а момент инерции принимают постоянным, равным среднему значению.

Момент инерции передаточного механизма в большинстве своем неизвестен, поэтому его принимают равным (10-30)% от момента инерции ротора электродвигателя, т.е.

J_ПМ=(0,1÷0,3)J_Д

В общем случае суммарный момент инерции электропривода, приведенный к валу электродвигателя, вычисляются по формуле:

J=(1,1÷1,3)J_Д+