
- •1.Классфификация кинематических цепей
- •2.Виды нагрузок электропривода и их классификация
- •3. Обобщенные математические модели механической части эп
- •Математическая модель и структурная схема двухмассовой модели эп.
- •5.Передаточные функции двухмассовой модели
- •6.Динамические свойства двухмассовой модели эп
- •7 .Модель,структурная схема и уравннеие движения одномассовой системы эп
- •9 .. Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для линейных пм
- •10.Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для нелинейных пм
- •13 Учет потерь в передаче.
- •14. Уточненный метод учета потерь в передаче.
- •11 Оптимальное передаточное число редуктора
- •По минимуму времени переходного процесса:
- •12Оптимальное передаточное числопо критерию минимум габарита эд
- •15. Статическая устойчивость работы эп
- •16.Механические переходные процессы эп при линейном динамическом моменте
- •18.Электромеханическая постоянная времени
- •20.Угол поворота вала электродвигателя за время переходного процесса.
- •21. Механические переходные процессы эп при нелинейном динамическом моменте
- •Теперь получаем дифференциальное уравнение:
- •С учетом (1.357) это уравнение принимает вид
- •При отсутствии диссипативных сил на основании (1.385) получаем
- •25.Уравнения напряжений, потокосцеплений и электромагнитного момента оэм.
- •26.Электромеханическая связь в эп
- •30. Модель оэм в осях u-V и её уравнения напряжений,потокосцепдений
- •31.Выражения электромагнитного момента оэм через скалярные величины и пространственные векторы.
- •33. Эквивалентная схема оэм в осях X-y для установившегося режима работы
- •Поскольку
- •34. Фазные преобразования переменных
- •Для трехфазной трехпроводной системы
- •35. Инвариантность мощности в преобразованиях уравнений оэм от осей к осям u-V
- •36 Режимы работы электродвигателей и ограничения на электромеханические преобразования энергии
- •37. Модель дпт нв в осях и её уравнения
- •38. Математическая модель дпт нв и структурная схема дпт нв в осях
- •40. Статические характеристики дпт нв
- •43 Математическая модель дпт пв в осях α–β.
- •44.Структурная схема линеаризованной модели дпт пв
- •45.Статические характеристики дпт пв при ненасыщенной магнитной системе.
- •47. Тормозные режимы работы дпт пв
- •48. Математическая модель дпт св в осях а-в
- •49. Статические характеристики дпт св
- •52. Статические характеристики ад. Механическая хар-ка и полная механическая мощность ад.
- •54. Влияние параметров на свойство и механическую характеристику ад
- •53. Электромеханические характеристики ад.
- •55. Характеристики и свойства асинхронного двигателя при питании от источника тока.
- •56.. Структурная схема линеаризованного ад при питании от источника напряжения.
- •58. Тормозные режимы ад: рекуперативное торможение и торможение противовключением
- •57.. Динамическое торможение ад при независимом возбуждении.
- •39.Уравнения , электромеханические и механические характеристики дпт нв при постоянном магнитном потоке. Структурная схема дпт нв
- •1. 1.Классфификация кинематических цепей 1
30. Модель оэм в осях u-V и её уравнения напряжений,потокосцепдений
Матричное уравнение электрического равновесия обмоток статора в осях u- :
 .
.
Заметим, что это уравнение не содержит переменных периодических коэффициентов, но имеет дополнительную ЭДС
 ,
,
обусловленную
вращением осей координат 1u-1
с угловой скоростью
 .
.
Уравнение электрического равновесия обмоток ротора в осях u- :
 .
.
Это уравнение также не имеет периодических коэффициентов, но включает дополнительную ЭДС
 ,
,
обусловленную
вращением осей ротора u-
относительно статора с угловой скоростью
 .
.
Полученные уравнения можно записать в проекциях на оси u- :
 ,
,

Потокосцепление рассматриваемой модели ОЭМ (Рис. 2.4)
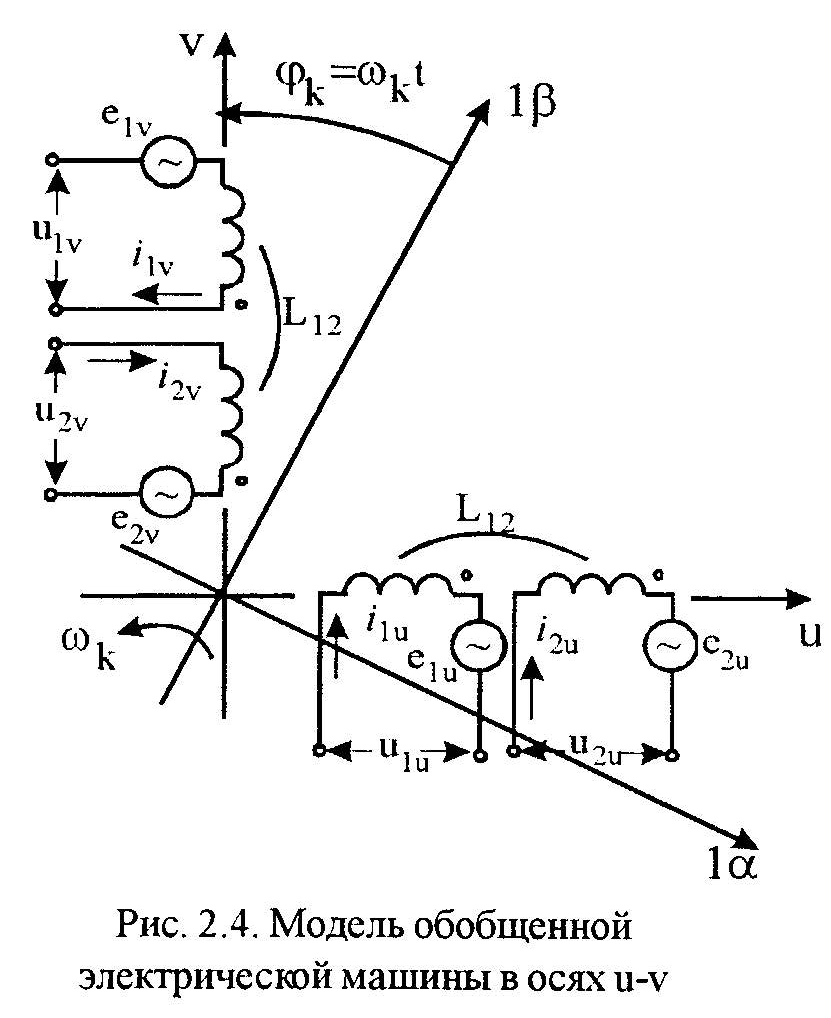

с учетом соотношений:
L1u,1u=L1,1=L1; L2u,2u=L2,2=L2 ,L1u,1=L1,1u=0; L2u,2=L2,2u=0 ,
L1u,2u=L2u,1u=L1,2=L2,1=L12
можно представить в виде
 (2.89)
где
(2.89)
где
 (2.90)
(2.90)
 (2.91)
(2.91)
 (2.92)
(2.92)
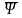 – вектор
потокосцепления,
– вектор
потокосцепления, – вектор тока,L – матрица
индуктивностей.
– вектор тока,L – матрица
индуктивностей.
Умножая (2.92) на (2.91), находим вектор потокосцеплений
 (2.93)
(2.93)
Вектор
потокосцеплений
целесообразно представить в виде суммы
вектора потокосцепления статора
 и вектора потокосцепления ротора
и вектора потокосцепления ротора
 ,
т.е.
,
т.е.
 ,
где
,
где
 ,
,
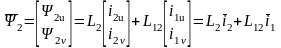 ,
,


Электромагнитный момент ОЭМ определим на основании равенства
 ,
где
,
где 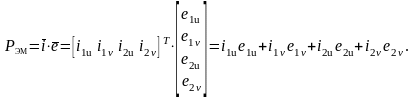
Подставляя
в (2.100) значения
 из (2.71) и
из (2.71) и
 из (2.80), получаем
из (2.80), получаем
 (2.101)
(2.101)
 (2.108)
(2.108)
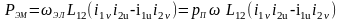 (2.109)
(2.109)
Здесь уместно заметить, что электромагнитная мощность ОЭМ не связана с вращением координат, а определяется только вращением ротора.
u-ν:

31.Выражения электромагнитного момента оэм через скалярные величины и пространственные векторы.
Выражение электромагнитного момента (2.110 ) можно записать через определитель:
 (2.111)
(2.111)
где
,
 ,
,
 – орты декартовой системы координат.
– орты декартовой системы координат.

Следовательно,
электромагнитный момент ОЭМ можно
рассматривать как вектор, направленный
вдоль орта
,
который перпендикулярен плоскости (
,
),
где расположены векторы токов
 и
и
 (рис. 2.5). Применительно к модели ОЭМ орты
,
расположены в плоскости, перпендикулярной
оси ротора. Таким образом, вектор
электромагнитного момента направлен
вдоль оси ротора ОЭМ. Величина
электромагнитного момента
(рис. 2.5). Применительно к модели ОЭМ орты
,
расположены в плоскости, перпендикулярной
оси ротора. Таким образом, вектор
электромагнитного момента направлен
вдоль оси ротора ОЭМ. Величина
электромагнитного момента
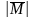 определяется площадью параллелограмма,
образованного векторами
и
:
определяется площадью параллелограмма,
образованного векторами
и
:
 (2.112)
(2.112)
Векторное произведение векторов тока и может быть представлено в матричной форме:
 (2.113)
(2.113)
где
 ,
(2.114)
,
(2.114)
 – кососимметричная матрица вектора
тока
.
– кососимметричная матрица вектора
тока
.
Рассмотрим другие выражения электромагнитного момента ОЭМ через пространственные векторы. Из (2.95) ) находим
 (2.115)
(2.115)
и подставляем в (2.111):
 (2.116)
(2.116)
так
как
 =0.
=0.
Из (2.96) определяем
 (2.117)
(2.117)
и подставляем в (2.111):
 (2.118)
(2.118)
так
как
 =0.
=0.
Используя
(2.96)
 ),
выражаем
),
выражаем
 (2.119)
(2.119)
и подставляем в (2.111):
 (2.120)
(2.120)
где
Kr
=
 ,(2.121)
Kr
– коэффициент магнитной связи ротора.
,(2.121)
Kr
– коэффициент магнитной связи ротора.
Теперь
из (2.95)
 )
находим
)
находим
 (2.122)
и подставляем в (2.111):
(2.122)
и подставляем в (2.111):

где
Ks
=
 ,
(2.124) Ks
– коэффициент магнитной связи статора.
,
(2.124) Ks
– коэффициент магнитной связи статора.
Из (2.95) и (2.96) следует, что
 (2.125)
(2.125)
Равенство (2.125) позволяет найти ток
 (2.126)
(2.126)
подстановка которого в (2.123) дает выражение электромагнитного момента ОЭМ через векторное произведение потокосцеплений:
 (2.127)
(2.127)
Выразим
потокосцепление статора как сумму
потокосцепления взаимоиндукции
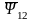 и потокосцепления рассеяния статора
и потокосцепления рассеяния статора
 :
:
 (2.128)
(2.128)
где
 – индуктивность рассеяния обмотки
статора.
– индуктивность рассеяния обмотки
статора.
Подстановка (2.128) в (2.116) приводим к результату
 (2.129)
(2.129)
так как =0. Аналогично имеем для потокосцепления ротора
 (2.130)
(2.130)
подстановка которого в (2.118) дает выражение

Выражения электромагнитного момента (2.129) и (2.131) показывают, что потоки рассеяния не участвуют в создании электромагнитного момента ОЭМ.
1)
 2)
2)
 3)
3)

4)
5)
 6)
6)
7)
 8)
8)
 Во
всех приведенных выражениях вектор
электромагнитного момента направлен
в одну сторону.
Во
всех приведенных выражениях вектор
электромагнитного момента направлен
в одну сторону.
32. КОМПЛЕКСНО-ВЕКТОРНЫЕ УРАВНЕНИЯ ОЭМ В ОСЯХ u-v, d-q,x-y
Оси координат u-ν можно расположить в комплексной плоскости, направив ось u вдоль положительной вещественной оси +Re, а ось ν – вдоль положительной мнимой оси +Im (или +j). В этом случае пять уравнений ОЭМ:
 (2.132)
(2.132)
можно записать в комплексно-векторной форме
 (2.133)
(2.133)
 (2.134)
(2.134)
 (2.135)
(2.135)
где
 (2.136)
(2.136)
Найдем
 (2.137)
(2.137)
Составляя (2.136) с выражением М в (2.132), видим, что

Поэтому приведенные выше уравнения электромагнитного момента ОЭМ, выраженные через пространственные векторы
1) ;2) ;3) ;
4) ;5) ;6)
7)
;8)
,
в комплексно-векторной форме будут
иметь такой вид (при одном и том же
направлении вектора
![]() ):
):
1)
,
2)
 ,
3)
,
3)
 ,
,
4)
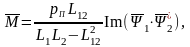 5)
5)
 6)
6)

7)
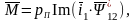 8)
8)
 .
.
Здесь символ * означает комплексно-сопряженную величину.
На практике наибольшее распространение получили три системы координат, в которых рассматриваются уравнения ОЭМ.
1) Неподвижная относительно статора система координат α-β.
В этом случае:
ωК=0; u=α; ν=β, φК=0
тогда на основании (2.133)-(2.135) получаем комплексно-векторные уравнения:

2) Неподвижная относительно ротора система координат d-q.
В этом случае:
ωК=ωЭЛ; φК=φЭЛ; u=d; ν=q
и уравнения (2.133)-(2.135) принимают вид:
 (2.140)
(2.140)
3) Неподвижная относительно вращающегося магнитного поля система координат x-y.
В данном случае:
ωК=ω0
ЭЛ=ω1= ;
φК=ω1t=φ1;
u=x;
ν=y.
;
φК=ω1t=φ1;
u=x;
ν=y.
Комплексно-векторные уравнения (2.133)-(2.135) преобразуются к виду:
 (2.142)
(2.142)
