51.Метод непосредственного интегрирования.

Непосредственным интегрирование наз. интегрирование с помощью свойств 3,4 и 6 тождественно преобразований подынтегральной функции и таблицы основных интегралов.

52.Метод поднесения под знак дифференциала.

На практике часто встречаются интегралы вида: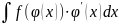 или интегралы, которые сводятся к такому виду.

Подведём в этом интеграле множитель ^’(x) под знак дифференциала:

^’(x) dx=d((x)), а затем произведём подстановку (x)= t.

В результате получаем формулу подстановки в неопределённом интеграле:

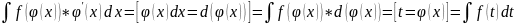
следовательно, задача свелась к нахождению интеграла 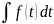, которые либо уже табличный, либо легко сводится к табличному, и обратный подстановке t=(x).

53. Метод интегрирования по частям.

Пусть u=u(x) и v=v(x) – дифференцируемые функции. Тогда справедлива следующая формула интегрирования по частям:

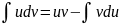
С помощью этой формулы вычисление интегра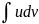ла сводится к отысканию другого интеграла .

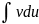Применение формулы целесообразно в тех случаях, когда интеграл более прост для нахождения, чем исходный либо подобен ему.

При этом в качестве u следует брать такую функцию, которая при дифференцировании упрощается, а в качестве dv – ту часть подынтегрального выражения интеграл от которого известен или может быть найден. Иногда формулу интегрирования по частям приходится применять несколько раз.

54.Основные типы простейших рациональных дробей.

1) А/х-а

2) А/(х-а)^к, (k  2, kN)

3) А/х²+рх+q, (D=p²-4q<0)

4) Ax+B/x²+px+q, (D=p²-4q<0)

5) Ax+B/(x²+px+q)^k, (k  2, kN, D=p²-4q<0)

где A, a, B, p, q  R.

55. Интегрирование рациональных дробей с помощью разложения их на простейшие дроби.

Перед интегрированием рациональной дроби 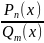, необходимо выполнить следующие алгебраические преобразования и вычисления.

1. Если дана неправильная рациональная дробь, выделить из неё целую часть, разделив числитель на знаменатель столбиком, т.е. представить эту дробь в виде:

,

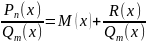где M(x) – многочлен, 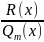– правильная рациональная дробь.

2. Разложить знаменатель дроби на линейные и квадратичные множители:

,

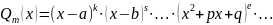где D=p²-4q<0.

3. Правильную рациональную дробь разложить на простейшие дроби:

,

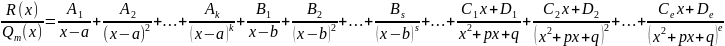где A_i, B_i, C_i, D_i, … - неизвестные пока что коэффициенты.

4. Вычислить неизвестные коэффициенты A_i, B_i, C_i, D_i, … к общему знаменателю, прировнять в числителе коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов.

Можно определить коэффициенты и другим способом придавая в полученном тождестве переменной х поочерёдно столько произвольных числовых значений, сколько неизвестных коэффициентов и решить систему.

56. Интегрирование иррациональных функций.

Интегралы вида

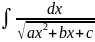
с помощью выделения полного квадрата

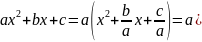
и последующей замены

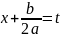
приводится к одному из интегралов:

1)

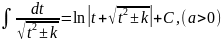
или

2)

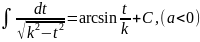
57.Интегрирование тригонометрических выражений с помощью универсальной тригонометрической подстановки.

1)Интеграл вида: 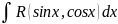приводит к интегрированию от рациональной функции с помощью универсальной тригонометрической подстановки: 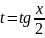. В результате получим: 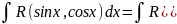2t/1+t², 1-t²/1+t²)*2dt/1+t²

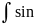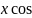2)Интеграл вида: ^{m n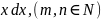} находят:

а) при нечётной n: t=sinx

б) при нечётной m: t=cosx

в) если m и n чётные: sinx*cosx=1/2sin2x sin²x=1/2(1-cos2x) cos²x=1/2(1+cos2x)

58.Свойства определённого интеграла.

1)

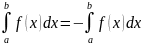
2)

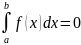
3)

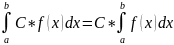
4)

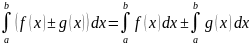
5)

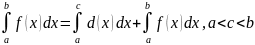
6)если

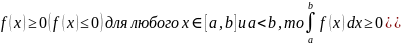
7) если

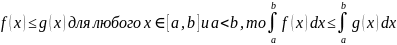
8) если f(x) интегрируема на отрезке [a,b] и для этого отрезка имеет место неравенство m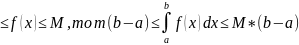

59.Методы вычисления определённого интеграла.

1) Формула Ньютона-Лейбница:

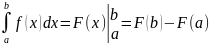
2) Замена переменной: а)

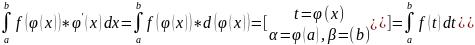
б)

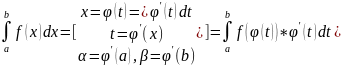
3) Интеграл по частям:

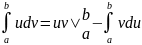
60.Применение определённого интеграла к вычислению площадей плоских фигур.

1)

2)

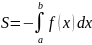
3)

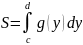
4)

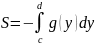
5)

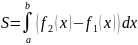
6)

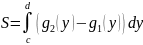
61. ДУ 1-го порядка с разделяющимися переменными.

ДУ 1-го порядка с разделяющимися переменными наз. уравнение вида:

P₁(x)  Q₁(y)dx+ P₂(x)  Q₂(y)dy=0, (*)

особенность которого в том, что коэффициент при dx и dy представляет собой произведение двух функций, одна из которых зависит только от х, а другая – только от у.

Замечание. Одна или несколько функций коэффициентов при dx и dy могут быть константой.

Для решения ДУ (*) нужно при dx убрать функцию, зависящую от y, т.е. Q₁(y), а при dy убрать функцию, зависящую от x, т.е. P₂(x). Для этого разделим обе зачти ДУ (*) на произведение этих «лишних» функций, т.е. на Q₁(y)dx  P₂(x)0.

, (**)

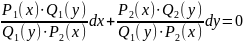
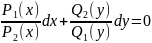В ДУ (**) при dx нет функции, зависящей от у, а при dy нет функции, зависящей от х.

Такое ДУ наз. ДУ с разделенными переменными, а процесс перехода от ДУ (*) к ДУ (**) наз. разделением переменных.

Проинтегрируем обе части ДУ (**).

и получим общий интеграл ДУ(*).

62. Однородные дифференциальные уравнения 1-го порядка.

Функция f(x,y) наз. однородной измерения n, если она удовлетворяет условию

f(tx, ty)=tⁿ  f(x,y).

1. Уравнение вида

P(x,y)dx+Q(x,y)dy=0, (*)

наз. однородным, если P(x,y) и Q(x,y) – однородные функции одного измерения.

2. Уравнение вида

y^’= f(x,y), (**)

наз. однородным, если функция f(x,y) является функцией нулевого измерения.

63. Линейные ДУ 1-го порядка. Уравнение Бернулли. Метод Бернулли.

ДУ 1-го порядка наз. линейным, если его можно записать в виде

y^’+p(x)  y=g(x), (*) где р(х) и g(х) – заданные функции.

Особенность ДУ (*) в том, что искомая функция у и её производная у^’ входят в ДУ первой степени, не перемножаясь между собой.

Уравнение Бернулли. y^’+p(x)  y=g(x)  yⁿ, n 0, n 1.

Метод Бернулли. Решение ДУ (*) ищется в виде

y= u  v, (**)

где u=u(x) и v=v(x) – две неизвестные функции. Из равенства (**) следует

y^’=(u  v)^’*u^’v+uv^’

Подставляя выражения у и у^’ в уравнение (*), получим:

u^’v+uv^’+p(x)  uv=q(x) или u^’v+u(v^’+p(x)v)=q(x). (***)

Первую неизвестную функцию v=v(x) подберём так, чтобы выражение в скобках было равно нулю, т.е. решим уравнение

v^’+p(x)v=0, которое является ДУ с разделяющимися переменными.

dv/dx  p(x)v=0   dx

dv+p(x)vdx=0   v0

dv/v+p(x)dx=0

lnv+ p(x)dx=C

lnv = -  p(x)dx+C

Виду свободы выбора v(x) можно принять С=0 и получим выражение для v(x):

lnv = -  p(x)dx

v=e^{- p(x)dx}

Подставляя найденную функцию v(x) в уравнение (***), получим уравнение

u^’  e^{- p(x)dx}=q(x), которое тоже является ДУ с разделяющимися переменными.

du/dx  e^{- p(x)dx}=q(x)   dx

e^{- p(x)dx} du=q(x)  dx  e^{- p(x)dx} 0

du=q(x)  e^{ p(x)dx} dx

 du= q(x)  e^{ p(x)dx} dx+C

u= q(x)  e^{ p(x)dx} dx+C

Возвращаясь к переменной у, получим общее решение исходного ДУ (*):

y= u  v =( q(x)  e^{ p(x)dx} dx+C)  e^{- p(x)dx}.