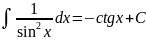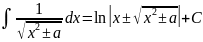- •1.Матрицы и их виды.
- •2.Сложение матриц и умножение на действительное число.
- •3.Согласованные матрицы. Умножение матриц и его свойства.
- •4.Элементарные преобразования матриц. Эквивалентные матрицы.
- •9.Невырожденная матрица. Союзная матрица. Обратная матрица. Теорема о существовании обратной матрицы.
- •10.Свойства обратной матрицы.
- •11.Ранг матрицы. Свойства ранга матрицы.
- •12. Системы линейных уравнений: однородные, неоднородные, совместные, несовместные, определённые, неопределённые.
- •13.Решение невырожденных систем линейных уравнений. Матричный метод. Формула Крамера. Метод Гаусса.
- •14.Совместность системы линейных уравнений. Теорема Кронекера-Капелли.
- •15.Однородные системы линейных уравнений. Условия существования тривиального и нетривиального решений системы линейных однородных уравнений.
- •16. Определение вектора. Линейные операции над векторами.
- •17.Проекция вектора на ось.
- •18.Базис. Разложение вектора по базису. Координаты вектора. Декартова система координат. Направляющие косинусы. Деление отрезка в данном отношении
- •19.Скалярное произведение векторов. Свойства скалярного произведения и его вычисление в ортонормированном базисе
- •20.Векторное произведение векторов. Свойства векторного произведения и его вычисление в ортонормированном базисе.
- •21.Смешанное произведение векторов. Свойства смешанного произведения и его вычисление в ортонормированном базисе.
- •22.Приложения смешанного произведения.
- •31. Определение предела функции в конечной точке и на бесконечности.
- •32. Основные теоремы о пределах.
- •33.Первый и второй замечательные пределы
- •34. Непрерывность функции. Классификация точек разрыва.
- •35.Определение производной функции в точке.
- •36. Геометрический смысл производной функции в точке.
- •38.Правила дифференцирования.
- •39. Производная сложной функции.
- •41.Логарифмическое дифференцирование.
- •42.Производные функций, заданных параметрическими уравнениями.
- •43.Дифференциал функции. Применение дифференциала к приближённым вычислениям.
- •44.Правило Лопиталя.
- •45.Возрастание и убывание функций. Точки экстремума функции.
- •46.Наименьшее и наибольшее значения функции на отрезке.
- •47.Выпуклость и вогнутость графика функции. Точки перегиба.
- •48. Асимптоты графика функции.
- •49. Общая схема исследования функции и построения графика.
- •50.Первообразная функции. Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов.
- •51.Метод непосредственного интегрирования.
- •52.Метод поднесения под знак дифференциала.
- •53. Метод интегрирования по частям.
- •54.Основные типы простейших рациональных дробей.
- •55. Интегрирование рациональных дробей с помощью разложения их на простейшие дроби.
- •64. Ду высших порядков, допускающие понижение порядка.
- •65. Линейные однородные ду 2-го порядка с постоянными коэффициентами. Структура общего решения в зависимости от корней характеристического уравнения.
- •66. Линейные неоднородные дифференциальные уравнения (лнду) 2-го порядка с постоянными коэффициентами. Структура общего решения.
- •67. Понятие функции двух переменных. Область определения.
- •68. Частные производные первого порядка. Полный дифференциал.
- •69. Частные производные высших порядков.
- •70.Экстремум функции двух переменных.
47.Выпуклость и вогнутость графика функции. Точки перегиба.
Определение 1. График дифференциальной функции y=f(x) наз. выпуклым в интервале (а,в), если он расположен ниже любой её касательной на этом интервале. График дифференциальной функции y=f(x) наз. вогнутым в интервале (а,в), если он расположен выше ниже любой её касательной на этом интервале.
Определение 2. Точка (Х0, f(X0), Х0 D(y) графика непрерывной ф-ции y=f(x), отделяя её выпуклую(вогнутую) часть от вогнутой(выпуклой) наз. её точкой перегиба.
48. Асимптоты графика функции.
Определение. Прямая L наз. асимптотой кривой y=f(x), если расстояние от точки M(x,y) кривой до прямой L стремится к нулю при неограниченном удалении этой точки по кривой от точки O(0;0) (т.е. при стремлении хотя бы одной из координат точки к ).
Асимптоты бывают вертикальные и невертикальные (наклонные и горизонтальные).
Утверждение 1. Прямая x=a явл. вертикальной асимптотой графика функции y=f(x), если
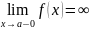
или
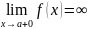
Т.е. для отыскания вертикальных асимптот нужно найти те значения x, вблизи которых функция f(x) неограниченно возрастает по модулю.
Замечание 1. Если
D(y)={(-;+) или [a;b] или (-;b] или [a;+)}, то вертикальных асимптот нет.
Замечание 2. Если
D(y)=(-;x1)(x1;x2)…(xn;+), то вертикальные асимптоты могут быть только прямые.
x=xi, i=1,…,n
(если
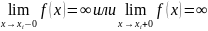 ).
).
Замечание
3.
Если D(y)=(a;+),
то вертикальная асимптотой может быть
только прямая x=a
(если

Замечание
4.
Если
D(y)=(-;b),
то вертикальной асимптотой может быть
только прямая x=b
(если
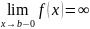
Утверждение 2. Если

и
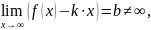
то y=kx+b – невертикальная асимптота. Причем k0 – наклонная, а при k=0 – горизонтальная асимптота.
49. Общая схема исследования функции и построения графика.
Схема полного исследования функции:
1) найти область определения функции;
2) найти (если это возможно) точки пересечения графика функции с осями координат;
3) выяснить, является ли функция чётной, нечётной или общего вида;
4) установить промежутки непрерывности функции, а также найти её точки разрыва;
5) найти вертикальные и невертикальные асимптоты (если они имеются);
6) найти интервалы монотонности и точки экстремума;
7) найти интервалы выпуклости (вогнутости) и точки перегиба;
8) найти пределы функции при x, стремящемся к концам области определения;
9) построить график функции.
50.Первообразная функции. Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов.
Определение1. Функция F(x) наз. первообразной функции f(x), заданной на некотором множестве Х, если для любого х Х выполняется равенство: F'(x)=f(x).
Определение2.
Множество
F(x) + C всех первообразной функции f(x) на
множестве Х наз. неопределённым интегралом
и обозначается:
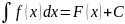
Нахождение первообразной для данной функции f(x) наз. интегрированием функции f(x).
Теорема. Для всякой непрерывной на интервале (а,в) функции f(x) существует на этом промежутке первообразная, а значит и неопределённый интеграл.
Геометрический неопределённый интеграл представляет собой семейство кривых, зависимых от одного параметра С, который получает одна из другой путём параллельного сдвига вдоль оси Оу.
Свойства:
1)(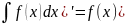
2)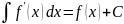
3)
4)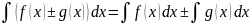
5)Если

6)Если
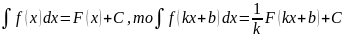
Таблица основных неопределённых интегралов:
1. |
6.
|
11. |
2.
|
7.
|
12.
|
3. |
8. |
13.
|
4. |
9. |
14.
|
5. |
10.
|
15.
|

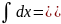 x + C
x + C x
dx = ax
/ ln a +C
x
dx = ax
/ ln a +C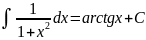

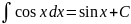
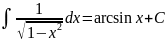
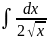 =
=
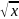 + C
+ C
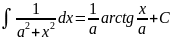
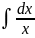 = ln
= ln
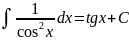
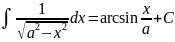
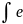 x
dx = ex
+C
x
dx = ex
+C