42.Производные функций, заданных параметрическими уравнениями.
Пусть функция y=f(x) задана параметрически в виде уравнения:
x=x(t),
y=y(t), t[,],
где t – вспомогательная переменная, называемая параметром.
По
правилу дифференцирования обратной
функции имеем:
.
(*)
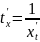Тогда функция y=f(x), определяемую параметрическими уравнениями можно рассматривать как сложную функцию y=y(t)’, где t=(x).
По
правилу дифференцирования сложной
функции имеем:
.
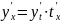С учетом равенства (*), получаем:
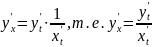
43.Дифференциал функции. Применение дифференциала к приближённым вычислениям.
=
f(x)(1).
Тогда
из (1) имеем:
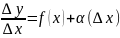(2).
Умножив
обе части на
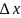получим:
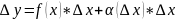(3).
Дифференциал
функции y=f(x) в точке Х
наз.
главной линейной частью
f’(x)
*
x
её
приращения
у,
и обозначается dy
или df(x):
dy=f(x)* x (4).
Если формулу (4) применить к самому аргументу Х, т.е. к функции y=f(x)=x, то учитывается что х'=1 получим: dx= x (5). Учитывая равенство (5), формулу (4) можно записать в виде: dy=f’(x) * dx (6).
Из
формулы (3) следует, что если f’(x)
0,
то при
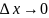в фиксированной точке х=х0
будет
выполняться:
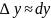или
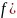x0
+
x)
– f
(x0)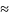
f
(x0
-
)
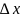(7).
44.Правило Лопиталя.
Пусть функция f(x) и g(x) дифференцированны в окрестные точки Х0 и g’(x) .
Если
,
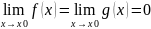
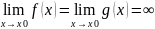т.е. частное f(x)/g(x) представляет собой
неопределённость вида 0/0 или
,
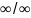то
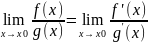при
условии что существует.
Замечание1.
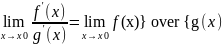
Замечание2.
Неопределённость
вида
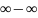приводится к неопределённому пределу
,
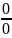а неопред. вида 0
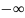к
неопред. виду
или
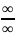путём
алгебраических преобразований
исследования функции.
45.Возрастание и убывание функций. Точки экстремума функции.
Определение1
Функция y=f(x) наз. возрастающей в интервале
(а,в), если для любого Х1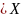
2,
где Х1,Х2
(а,в),
выполняется условие f(X1)
f(X2).
Определение2 Функция y=f(x) наз. убывающей в интервале (а,в), если для любого Х1 Х2, где Х1,Х2 (а,в) выполняется след. условие f(X1) f(X2).
Возрастание или убывание в некотором интервале (а,в), функция наз. монотонной в этом интервале.
Теорема1
Если
ф-ция y=f(x) дифференцирован в интервале
(а,в) и f'(x)
0
при всех Х
(а,в),
то функция f(x)
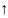в интервале (а,в), но если f’(x)<0
при всех Х
(а,в),
то ф-ция f(x)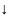
в интервале(а,в).
Определение3 Точка Х0 наз. min функции y=f(x), если существует такая -окрестность V(X0,v) точки Х0 что для любого Х V(X0,v) выполняется неравенство f(x0)<f(x). Если же для любого х V(X0,v) выполняется неравенство f(x0) > f(x), то точка Х0 наз. точкой max.
При этом число f(X0) наз. min(max) функции. Точки min(max) наз. её точками экстремума.
Теорема2 Если функция y = f(x)в точке x0 имеет экстремуму, то f’(x)=0 или f’(x) не существует.
Теорема3
Пусть функция y
= f(x)
дифференцирова в некоторой v - окресности
V(x0,v)=(x0-v,
x0+v)
точки X0
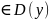за исключением могут быть самой точки
Х0.
Если
f’(x)>0
для любого x
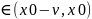и f’(x)<0
для любого х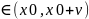
.
Теорема4 Пустьf’(x0)=0 или f”(x0) . Тогда функция y = f(x) имеет в точке Х0 max, если f”(x0)<0 и min, если f”(x0)>0.
46.Наименьшее и наибольшее значения функции на отрезке.
Алгоритм нахождения наименьшего и наибольшего значений функции на отрезке (а,в):
1. найти критические точки функции, оставить для рассмотрения только те из них, которые на интервале (а,в)
2. вычислить значения функции в найденных критических точках
3. вычислить значения функции на концах отрезка при х=а и х=в
4.среди всех вычисленных значений функции выбрать наименьшее и наибольшее