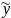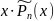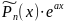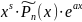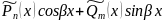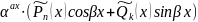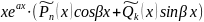- •1.Матрицы и их виды.
- •2.Сложение матриц и умножение на действительное число.
- •3.Согласованные матрицы. Умножение матриц и его свойства.
- •4.Элементарные преобразования матриц. Эквивалентные матрицы.
- •9.Невырожденная матрица. Союзная матрица. Обратная матрица. Теорема о существовании обратной матрицы.
- •10.Свойства обратной матрицы.
- •11.Ранг матрицы. Свойства ранга матрицы.
- •12. Системы линейных уравнений: однородные, неоднородные, совместные, несовместные, определённые, неопределённые.
- •13.Решение невырожденных систем линейных уравнений. Матричный метод. Формула Крамера. Метод Гаусса.
- •14.Совместность системы линейных уравнений. Теорема Кронекера-Капелли.
- •15.Однородные системы линейных уравнений. Условия существования тривиального и нетривиального решений системы линейных однородных уравнений.
- •16. Определение вектора. Линейные операции над векторами.
- •17.Проекция вектора на ось.
- •18.Базис. Разложение вектора по базису. Координаты вектора. Декартова система координат. Направляющие косинусы. Деление отрезка в данном отношении
- •19.Скалярное произведение векторов. Свойства скалярного произведения и его вычисление в ортонормированном базисе
- •20.Векторное произведение векторов. Свойства векторного произведения и его вычисление в ортонормированном базисе.
- •21.Смешанное произведение векторов. Свойства смешанного произведения и его вычисление в ортонормированном базисе.
- •22.Приложения смешанного произведения.
- •31. Определение предела функции в конечной точке и на бесконечности.
- •32. Основные теоремы о пределах.
- •33.Первый и второй замечательные пределы
- •34. Непрерывность функции. Классификация точек разрыва.
- •35.Определение производной функции в точке.
- •36. Геометрический смысл производной функции в точке.
- •38.Правила дифференцирования.
- •39. Производная сложной функции.
- •41.Логарифмическое дифференцирование.
- •42.Производные функций, заданных параметрическими уравнениями.
- •43.Дифференциал функции. Применение дифференциала к приближённым вычислениям.
- •44.Правило Лопиталя.
- •45.Возрастание и убывание функций. Точки экстремума функции.
- •46.Наименьшее и наибольшее значения функции на отрезке.
- •47.Выпуклость и вогнутость графика функции. Точки перегиба.
- •48. Асимптоты графика функции.
- •49. Общая схема исследования функции и построения графика.
- •50.Первообразная функции. Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов.
- •51.Метод непосредственного интегрирования.
- •52.Метод поднесения под знак дифференциала.
- •53. Метод интегрирования по частям.
- •54.Основные типы простейших рациональных дробей.
- •55. Интегрирование рациональных дробей с помощью разложения их на простейшие дроби.
- •64. Ду высших порядков, допускающие понижение порядка.
- •65. Линейные однородные ду 2-го порядка с постоянными коэффициентами. Структура общего решения в зависимости от корней характеристического уравнения.
- •66. Линейные неоднородные дифференциальные уравнения (лнду) 2-го порядка с постоянными коэффициентами. Структура общего решения.
- •67. Понятие функции двух переменных. Область определения.
- •68. Частные производные первого порядка. Полный дифференциал.
- •69. Частные производные высших порядков.
- •70.Экстремум функции двух переменных.
64. Ду высших порядков, допускающие понижение порядка.
ДУ порядка выше 1-го наз. ДУ высших порядков.
Отдельные виды ДУ высших порядков удается проинтегрировать путём понижения порядка уравнения.
1. Уравнение вида
y(n)=(x), решают путём n – кратного интегрирования.
2. Уравнение вида
F(x, y(k), y(k+1),…, y(n))=0, явно не содержащее искомой функции и её первых производных до k-1 включено, сводят к уравнению порядка n-k путём введения новой неизвестной функции z=z(x), пологая z=y(k). Тогда уравнение примет вид
F(x, z, z’,…, z(n-k))=0.
3. Уравнение вида
F(y, y’, y’’,…, y(n))=0, явно не содержащее независимой переменной х, интегрируют с помощью подстановки y’=p, где р=р(у) – новая неизвестная функция, а за аргумент временно примем переменную у. Тогда
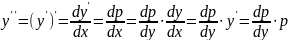 ,
,
т.е.
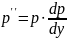 .
.
Аналогично можно получит
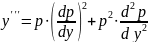 и
т. д.
и
т. д.
При этом порядок уравнения понижается на единицу.
65. Линейные однородные ду 2-го порядка с постоянными коэффициентами. Структура общего решения в зависимости от корней характеристического уравнения.
Уравнение вида
a2y’’+a1y’+a0y=0, (*)
где aiR, i=0, 1, 2, наз. линейным однородным (ЛОДУ) 2-го порядка с постоянным коэффициентом.
Теорема. (структура общего решения ЛОДУ 2-го порядка). Если два частных решения y1=y1(x) и y2=y2(x) ЛОДУ (*) образуют на интервале (а;b) фундаментальную систему, то общим решением этого уравнения явл. функция
y=C1y1+C2y2 , (**)
где С1 и С2 – произвольные постоянные.
Т. о. для нахождения общего решения ЛОДУ (*) достаточно найти два его частных решения образующих фундаментальную систему.
Будем искать частные решения уравнения (*) в виде y=ex, где - некоторое число (Л. Эйлер).
Дифференцируем эту функцию два раза и подставляя выражение для y, y’, y’’ в уравнение (*), получим:
a22ex+a1 ex+a0 ex=0 ex 0
a22+a1+a0=0, (***).
Уравнение (***) наз. характеристическим уравнением (х. у) ЛОДУ (*) (для его составления достаточно в уравнении (*) заменить y’’, y’, y на 2, , 1 соответственно).
При решении х. у. (***) возможны следующие три случая:
1) D>0;
2) D=0;
3) D<0.
66. Линейные неоднородные дифференциальные уравнения (лнду) 2-го порядка с постоянными коэффициентами. Структура общего решения.
Уравнение вида
a2y’’+a1y’+a0y= f(x), (*)
где a1R, i=0, 1, 2 f(x) – непрервная на некотором интервале (а;b) функции.
Правая часть f(x) |
Корни характеристического уравнения |
Вид
частного решения
|
Pn(x) |
1. Число 0 не явл. корнем х. у. |
|
2. Число 0 – корень х. у. |
|
|
Pn(x) eax |
1. Число a не явл. корнем х. у. |
|
2. Число a – корень х. у. |
|
|
Pn(x)cosx+Qm(x)sinx |
1. Число i не явл. корнем х. у. |
|
2. Число i – корень х. у. |
|
|
ax (Pn(x)cosx+Qk(x)sinx) |
1. Число не явл. корнем х. у. |
|
2. Число – корень х. у. |
|
Замечание 1. k=max(m, n).
Замечание 2.

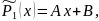

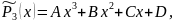 и
т. д.,
и
т. д.,
где A, B, C, D, … - неизвестные коэффициенты, которые находят подстановкой в уравнение (*) и приравниванием коэффициентов при одноимённых функциях в левой и правой частях равенства.