10.Свойства обратной матрицы.

Свойства:

1) det (A^-1) =1/detA

2) (AB)^-1=A^-1×B^-1

3) (A^-1)^T=(A^T)^-1

11.Ранг матрицы. Свойства ранга матрицы.

Рангом матрицы наз. наибольший из порядков, отличный от 0 миноров этой матрицы. (rA или rangA)

Свойства ранга матрицы:

1)ранг матрицы не меняется при трансформировании

2)ранг матрицы не изменится, если из неё вычеркнуть нулевой ряд

3)если у матрицы есть несколько одинаковых, пропорциональных, параллельных рядов, то можно 1 из них оставить, остальные вычеркнуть, ранг не изменится.

4)ранг матрицы не меняется при элементарных преобразованиях

12. Системы линейных уравнений: однородные, неоднородные, совместные, несовместные, определённые, неопределённые.

Дана система m линейных алгебраических уравнений с n неизвестных

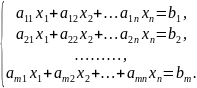
Где числа a_n-коэффициенты системы, а числа b_i-свободные члены.

Если все b_i=0 (свободные члены), то система называется однородной, в противном случае – неоднородной.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной – если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение. Система, имеющая более одного решения наз. неопределённой.

13.Решение невырожденных систем линейных уравнений. Матричный метод. Формула Крамера. Метод Гаусса.

Матричный метод

Записать систему в матричном виде АХ=В. Умножим обе части последнего матричного уравнения слева на матрицу А^-1.Поскольку А^-1×А = Е и ЕХ=Х, то формула для нахождения столбца их неизвестных примет вид: Х = А^-1×В

Формула Крамера

Введём следующие обозначения:

, ,

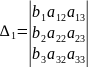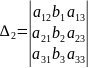т.е. определители ∆₁, ∆₂, ∆₃, получаются из определителя ∆ путём замены его 1,2 и 3 столбцов соответственно столбцом свободных членов, тогда единственное решение системы может быть найдена по формуле Крамера: х₁=∆₁/∆, х₂=∆₂/∆, х₃=∆₃/∆.

Метод Гауса

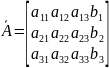
С помощью элементарных преобразований над строками приведём матрицу к трапецеидальному виду:

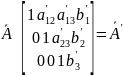
Далее запишем систему линейных уравнений, которая соответствует расширенной матрице А :

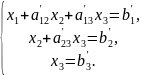
из которых последовательно и найдём искомое решение.

14.Совместность системы линейных уравнений. Теорема Кронекера-Капелли.

Теорема Кронекера-Капелли

Для того, чтобы система была совместной , необходимо и достаточно, чтобы ранг матрицы А был равен рангу её расширенной матрицы Ā. Если ранг матрицы А= рангу матрицы Ā и равен числу неизвестных, то система имеет единственное решение. Если ранг матрицы А = рангу матрицы Ā, но меньше числа неизвестных то система имеет бесконечное множество решений.

15.Однородные системы линейных уравнений. Условия существования тривиального и нетривиального решений системы линейных однородных уравнений.

Однородная система всегда совместна, т.к. ранг её матрицы = рангу расширенной матрицы .Набор чисел: Х₁= …=Х_n=0, всегда явл. решением однородной системы.

Теорема1. Однородная система имеет лишь тривиальное решение только тогда, когда ранг основной матрицы системы равен числу неизвестных, т.е. rangA= n.

Теорема 2. Для того, чтобы система однородных уравнений имела ненулевые решения , необходимо и достаточно, чтобы ранг её основной матрицы был меньше числа неизвестных, т.е. rangA<n.