
- •1.Матрицы и их виды.
- •2.Сложение матриц и умножение на действительное число.
- •3.Согласованные матрицы. Умножение матриц и его свойства.
- •4.Элементарные преобразования матриц. Эквивалентные матрицы.
- •9.Невырожденная матрица. Союзная матрица. Обратная матрица. Теорема о существовании обратной матрицы.
- •10.Свойства обратной матрицы.
- •11.Ранг матрицы. Свойства ранга матрицы.
- •12. Системы линейных уравнений: однородные, неоднородные, совместные, несовместные, определённые, неопределённые.
- •13.Решение невырожденных систем линейных уравнений. Матричный метод. Формула Крамера. Метод Гаусса.
- •14.Совместность системы линейных уравнений. Теорема Кронекера-Капелли.
- •15.Однородные системы линейных уравнений. Условия существования тривиального и нетривиального решений системы линейных однородных уравнений.
- •16. Определение вектора. Линейные операции над векторами.
- •17.Проекция вектора на ось.
- •18.Базис. Разложение вектора по базису. Координаты вектора. Декартова система координат. Направляющие косинусы. Деление отрезка в данном отношении
- •19.Скалярное произведение векторов. Свойства скалярного произведения и его вычисление в ортонормированном базисе
- •20.Векторное произведение векторов. Свойства векторного произведения и его вычисление в ортонормированном базисе.
- •21.Смешанное произведение векторов. Свойства смешанного произведения и его вычисление в ортонормированном базисе.
- •22.Приложения смешанного произведения.
- •31. Определение предела функции в конечной точке и на бесконечности.
- •32. Основные теоремы о пределах.
- •33.Первый и второй замечательные пределы
- •34. Непрерывность функции. Классификация точек разрыва.
- •35.Определение производной функции в точке.
- •36. Геометрический смысл производной функции в точке.
- •38.Правила дифференцирования.
- •39. Производная сложной функции.
- •41.Логарифмическое дифференцирование.
- •42.Производные функций, заданных параметрическими уравнениями.
- •43.Дифференциал функции. Применение дифференциала к приближённым вычислениям.
- •44.Правило Лопиталя.
- •45.Возрастание и убывание функций. Точки экстремума функции.
- •46.Наименьшее и наибольшее значения функции на отрезке.
- •47.Выпуклость и вогнутость графика функции. Точки перегиба.
- •48. Асимптоты графика функции.
- •49. Общая схема исследования функции и построения графика.
- •50.Первообразная функции. Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов.
- •51.Метод непосредственного интегрирования.
- •52.Метод поднесения под знак дифференциала.
- •53. Метод интегрирования по частям.
- •54.Основные типы простейших рациональных дробей.
- •55. Интегрирование рациональных дробей с помощью разложения их на простейшие дроби.
- •64. Ду высших порядков, допускающие понижение порядка.
- •65. Линейные однородные ду 2-го порядка с постоянными коэффициентами. Структура общего решения в зависимости от корней характеристического уравнения.
- •66. Линейные неоднородные дифференциальные уравнения (лнду) 2-го порядка с постоянными коэффициентами. Структура общего решения.
- •67. Понятие функции двух переменных. Область определения.
- •68. Частные производные первого порядка. Полный дифференциал.
- •69. Частные производные высших порядков.
- •70.Экстремум функции двух переменных.
16. Определение вектора. Линейные операции над векторами.
Вектором называется направленный отрезок, т.е. отрезок, имеющий определённую длину и определённое направление.
Под линейными операциями над векторами понимают:
а) произведение вектора на число;
б) сложение и вычитание векторов.
Произведением
вектора
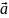 на
число R
наз.
вектор
,
удовлетворяющий следующим условиям:
на
число R
наз.
вектор
,
удовлетворяющий следующим условиям:
1)
длина вектора
равна произведению модуля числа
на длину вектора
:
 ;
;
2) вектор коллинеарен вектору : направление вектора совпадает с направление вектора , если >0, и противоположно ему, если <0.
Сложение двух векторов можно производить по правилам:
1) параллелограмма;
2) треугольника.
Правило
параллелограмма.
Пусть даны два произвольных вектора
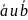 :
:
Выберем произвольную точку О и перенесём векторы так, чтобы их начало оказалось в точке О.
Правило
треугольника.
Пусть
– два произвольных вектора. Возьмём
произвольную точку О и построим вектор
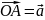 .
От точки А отложим вектор
.
От точки А отложим вектор
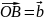 .
Вектор
.
Вектор
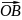 ,
соединяет начало первого вектора с
концом второго наз. суммой векторов
.
,
соединяет начало первого вектора с
концом второго наз. суммой векторов
.
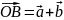 .
.
Сложение
трёх и более векторов
можно находить по правилу замыкания
ломаной. Чтобы найти сумму векторов
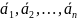 ,
нужно конец вектора
,
нужно конец вектора
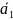 совместить с началом вектора
совместить с началом вектора
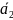 ,
конец вектора
,
совместить с началом вектора
,
конец вектора
,
совместить с началом вектора
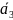 и т. д. пока не дойдём до вектора
и т. д. пока не дойдём до вектора
 .
Тогда суммой
будет вектор идущий из начала вектора
в конец вектора
.
.
Тогда суммой
будет вектор идущий из начала вектора
в конец вектора
.
Разностью
двух векторов
называется такой вектор
 ,
который
нужно сложить с вектором
,
который
нужно сложить с вектором
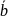 ,
чтобы
получить вектор
,
т.е.
,
чтобы
получить вектор
,
т.е.
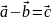
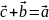 .
.
Чтобы
построить вектор
равный
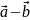 нужно
параллельным переносом перенести вектор
к
общему началу, и тогда вектор
будет
выходить из конца вектора
в
конец вектора
.
нужно
параллельным переносом перенести вектор
к
общему началу, и тогда вектор
будет
выходить из конца вектора
в
конец вектора
.
В параллелограмме, построенном на векторах одна направленная диагональ является суммой векторов, а другая разностью.
17.Проекция вектора на ось.
Осью наз. всякая прямая, на которой указано направление.
Проекцией точки М на ось наз. основание перпендикуляра, опущенного из точки М на данную ось.
![]()
Углом между вектором ĀВ или равным ему вектором СВ и осью Ох наз. угол α, на который нужно повернуть кратчайшем образом полуось Ох, до совмещения её с вектором СВ.
Область изменения угла α: 0≤α≤π.
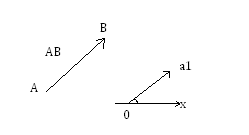
Проекцией вектора АВ на ось Ох наз. число, обозначаемое прОх АВ и /АВ/*cosα, где α- это угол между вектором Ав и осью Ох, т.е. по определению:
ПРОх АВ = /АВ/ * cos α
Геометрическая проекция вектора АВ на ось Ох = длине отрезка СД, взятой со знаком +, если 0≤α≤π/2 и со знаком минус , если π/2<α≤π. При α=π/2 отрезок СД превращается в точку и ПРОХ АВ = 0.
Свойства:
1.при умножении вектора АВ на число m, его проекция на ось умножается на то же число: прохАВ*m = m*прохАВ
2.проекция суммы двух векторов на ось, равна сумме проекции, соответствующих на ту же ось: прох (АВ + СД) = прох АВ + прох СД
18.Базис. Разложение вектора по базису. Координаты вектора. Декартова система координат. Направляющие косинусы. Деление отрезка в данном отношении
Базисом на плоскости наз. любых два некомпланарных вектора на этой плоскости, взятых в определённом порядке.
Теорема Если на плоскости выбран базис е1, е2, то любой вектор ā этой плоскости можно разложить по векторам е1, е2 и такое разложение единственное: ā = х * е1 + у * е2.
Базисом в пространстве наз. любые три некомпланарных вектора в этом пространстве, взятые в определённом порядке.
Теорема Если в пространстве выбран базис е1,е2,е3, то любой вектор ā этой плоскости (пространства) можно разложить по векторам е1, е2, е3 и такое разложение единственное: : ā = х * е1 + у * е2 + z * e3.
Свойства:
1)При умножении вектора ā (x, y, z) на число λ є R, все его координаты умножаются на это число: λ* ā = (λх, λу, λz)
2)При сложении(вычитании) векторов ā = (x, y, z) и в = (х2, у2, z2) складываются (вычитаются) их соответствующие координаты:
ā+-в = (х1+-х2, у1+-у2, z1+-z2)
Декартовой системой координат в пространстве наз. совокупность фиксированной точки О и базиса
![]() Точка
О наз.
началом координат, а
прямые,
проходящие через начало координат наз.
Точка
О наз.
началом координат, а
прямые,
проходящие через начало координат наз.
Прямая Ох наз. осью абсцисс, прямая Оу – осью ординат, прямая Оz – осью аппликат. Плоскости, проходящие через оси координат, наз. координатными плоскостями. Вектор ОМ для произвольной точки М, наз. её радиус вектором.
Координаты радиуса вектора точки М по отношению к началу координат наз. координатой точки М в рассматриваемой системе координат.
Базис наз. ортонормированным, если базисные векторы попарно ортогональны и длина каждого из них = 1. На плоскости ортонормированный базис принято обозначать: i=(1,0), j=(0,1), в пространстве i=(1,0,0), j=(0,1,0), k=(0,0,1).
Декартовая система координат с ортонормированным базисом наз. прямоугольной системой координат.
Деление отрезка в данном отношение:
Координаты точки М(х,у,z), лежащей на отрезке АВ и делящей этот отрезок в отношении λ, т.е.: АМ= λМВ, вычисляются по формулам деления отрезка в данном отношении: х = х1+λх2/1+λ, у = у1+λу2/1+λ, z = z1+λz2/1+λ
