31. Определение предела функции в конечной точке и на бесконечности.

Пусть функция y=f(x) определена в промежутке (-;+).

Определение. Число А наз. Пределом функции y=f(x) при x, если >0 существует такое число М>0, зависящее от , что при всех х, таких что 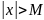выполняется .

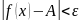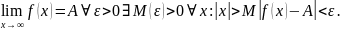
Геометрический смысл: при бесконечно больших значениях аргумента х график функции y=f(x) имеет свое горизонтальной асимптотой параллельную оси Ох прямую y=A, т.е. неограниченно близко приближается к этой прямой.

32. Основные теоремы о пределах.

Теорема. Если 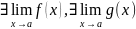и C-const, то:

1)

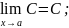
2) ;

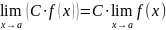3) ;

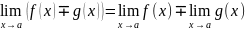4) ;

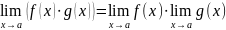5) ;

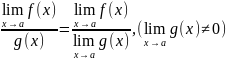6) ;

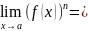7) .

При применении этой теоремы необходимо иметь в виду, что для любого не нулевого числа С справедливо:

1) С 0=0;

2) C 0=C;

3) ;

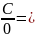4) ;

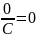5) C  =;

6) C ±  =;

7) 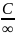= 0;

8) ;

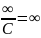9) 0 0=0;

10)    ;

11) ⁿ=, nN.

А если условие этой теоремы не выполняются, то могут возникнуть неопределённости вида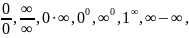 которые в простейших случаях раскрываются с помощью алгебраических преобразований данного выражения и отыскание предела в таких случаях наз. раскрытием неопределённостей.

Для всех основных элементарных функций в любой точке их области определения имеет место равенство

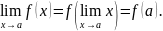
Это равенство можно понимать так: вычисление любого предела нужно начинать с непосредственной подстановки предельного значения, и если нет неопределённости, сразу записать ответ.

При нахождении пределов полезно иметь в виду следующие свойство показательной функции:

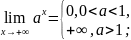
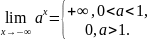
33.Первый и второй замечательные пределы

Замечательными ( в виду большого числа их применений) наз. => два предела:

Первый 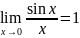применяется для распределения неопределённого вида %, при вычислении приделов содержащих тригонометрические функции.

Второй ^1/х = е применяется для раскрытия неопределённого вида 1∞.

34. Непрерывность функции. Классификация точек разрыва.

Пусть функция y=f(x) определена в V(x₀). Для x V(x₀)

x=x-x₀ называют приращением аргумента x в точке x₀;

а y=f(x)-f(x₀) – приращением функции в точке x₀.

Очевидно, что x и yмогут быть как положительными так и отрицательными.

Определение 1. Функция y=f(x) наз. непрерывной в точке x=x₀, если 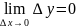, т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Определение 2. Функция y=f(x) наз. непрерывной в точке x=x₀, если

1) f(x) определена в точке x₀ и её окрестности;

2) 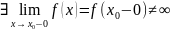и

;

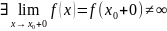3) f(x₀-0)=f(x₀+0)=A;

4) A=f(x₀).

Если функция y=f(x)непрерывна в каждой точке некоторого множества, то она наз. непрерывной на этом множестве.

Точка x=x₀ наз. точкой разрыва, если хотя бы одно из условий определения 2 не выполнено. Если нарушено условие 2, то точка x₀ наз. точкой разрыва второго рода; если нарушены условия 3 или 4, то точка x₀ наз. точкой разрыва первого рода (при нарушении условия 3) x₀ наз. точкой скачка и скачок равен f(x₀+0)- f(x₀-0), а при нарушении условия 4 x₀ наз. точкой устранимого разрыва.

35.Определение производной функции в точке.

Определение. Производной функции у=f(x) в точке Х₀ наз. предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0, если этот предел существует, т.е. у^’= .

Функция у=f(x), имеющая производную в каждой точке на промежутке Ч, наз. дифференцируемой на этом промежутке, операция нахождения производной наз. дифференцированием.

Теорема. Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.