67. Понятие функции двух переменных. Область определения.

Пусть каждой упорядоченной паре чисел (х, у) из некоторой области D соответствует определённое число zER. Тогда z=f(x, y) наз. функцией двух переменных х и у, х, у – независимыми переменными или аргументами, D – областью определения, а множество Е всех значений функции – областью её значений. Геометрически область определения функции z=f(x, y) представляет собой либо всю плоскость Оху, либо некоторую часть плоскости Оху ограниченную линиями, которые могут принадлежать или не принадлежать этой плоскости.

Линию, ограничивающую область наз. границей области. Точки области, не лежащие на границе наз. внутренними. Область состоящая только из одних внутренних точек наз. открытой. Область с присоединённой к ней границей наз. замкнутой, и обозначается .

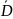68. Частные производные первого порядка. Полный дифференциал.

Пусть задана функция z=f(x, y). Зафиксируем значение у, при этом получим функцию одной переменной х. Дадим независимой переменной х приращение х, тогда z получит приращение, которое наз. частным приращением z по х и обозначается _xz.

Итак, _xz= f(x+x; y)-f(x; y).

Аналогично получим частное приращение z по у: _yz=f(x; y+y)-f(x; y).

Тогда частной производной 1-го порядка функции z=f(x, y) в точке M(x;y) по переменной х наз. предел (при условии, что он существует).

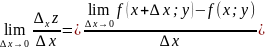
и обозначается одним из символов:

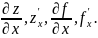
Аналогично определяется и обозначается частная производная 1-го порядка функции z=f(x, y) в точке M(x;y) по переменной у:

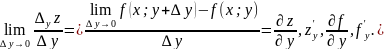
69. Частные производные высших порядков.

Частные производные 1-го порядка 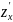и 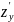можно рассматривать как функции от (x; y)D.

Эти функции могут иметь частные производные, которые наз. частными производными 2-го порядка. Они обозначаются и определяются следующим образом:

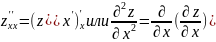
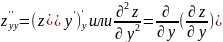
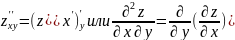
Аналогично определяется частные 3-го, 4-го и т.д. порядков.

Частная производная 2-го или более высокого порядка взятая по различным переменным наз. смешанной частной производной. Таковыми являются, например: :

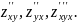Теорема. Если смешанные производные 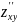и 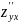непрерывны в рассматриваемой точке M(x, y), то 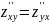(результат не зависит от порядка дифференцирования).

70.Экстремум функции двух переменных.

Теорема1. (необходимое условие сущ. экстремума). Если функция z=f(x,y) в точке (х₀, у₀) имеет локальный экстремума, то в этой точке обе част. Производные, если они существуют, =0 или хотя бы 1 из них в этой точке не существует.

Точки, которых част. производное 1-порядка = 0, наз. стационарным. Стационарные точки и точки в которых, хотя бы 1 частное производное не сущ. наз. критическими.

Равенство нулю частного производного яв. необходимым, но не достаточным условием сущ. экстремума. Для нахождения экстремума нужно каждую критическую точку подвергнуть дополнительному исследованию.

Теорема2. (достаточное условие сущ. экстремума). Пусть (х₀, у₀) – критическая точка, принадлежащая области определения функции z = f (x, y) и А=Z^”_хх(х_0, у₀), В=Z^»_xy(х_0, у₀), C= Z^»_yy(х_0, у₀).

Обозначим: 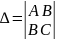=АС – В²

Тогда:1)если >0, то функция z = f(x, y) имеет в точке (х₀, у₀) экстремум: max, если А 0, min, если А 0.

2)если 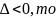функция z = f(x, y) имеет в точке (х₀, у₀) экстремума не имеет.

3)если 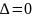экстремум в точке (х₀, у₀) может быть, может не быть. Необходимы дополнительные исследования.