4 Фигура.

Для четвёртой фигуры силлогизма получаем:

при этом

Не выписывая подробно промежуточные вычисления, сразу приведём вид выражения для S:

Значит, таблица Карно истинности для этого выражения:

Z	Y X	0	1
0	0	1	0
0	1	0	0
1	0	1	0
1	1	1	1

Сравнивая таблицы для S и , приходим к выводу, что условия импликации, не выполняются для двух дефектных блоков:

и

поэтому четвёртая фигура не является логическим законом, а её исправленный вид приводится в п.3.7 следующего параграфа.

Остальные виды сложных логических операций, которые подробно рассмотрены во многих учебных пособиях, мы оставляем для самостоятельного знакомства нашим читателям.

Контрольные вопросы:

1. Понятие о специальных видах сложных высказываний.

2. Строение фигур силлогизма.

3. Анализ первой фигуры силлогизма.

4. Анализ второй фигуры силлогизма.

5. Анализ третьей фигуры силлогизма.

6. Анализ четвёртой фигуры силлогизма.

7. Определение дефектных блоков фигур силлогизмов.

8. Методы исправления дефектных блоков.

Глава 4. Законы логики и их применение

§ 17. Законы математической логики.

Мы будем условно подразделять все законы логики по уровням, соответствующим вхождению первичных высказываний. Таким образом, мы рассмотрим унарные, бинарные и тернарные законы, а также переходные формы законов, отражающие расширение или сжатие исходной формулы. Существуют и законы более высоких уровней, но в данном пособии мы не будем их рассматривать. Если закон состоит из равенства (тождества) двух частей, то удобно рассматривать каждую часть отдельно и затем сравнивать формулы рабочих блоков или матрицы Карно этих частей. Их совпадение приводит к доказательству закона. Если закон представляет собой тавтологию, то есть всюду верное высказывание, то достаточно показать, что функция истинности этого высказывания равна единице. Если же закон имеет вид последовательности импликаций, то для его доказательства нужно построить соответствующие части: посылку (причину) и результат (следствие). Затем проводится сравнение матриц Карно этих высказываний для выявления правильности следования или же определения дефектных блоков. Перейдём к рассмотрению основных логических законов.

1. Унарные (однослойные) законы.

1.1. Закон непротиворечивости:

1.2. Закон тождества:

1.3.Закон исключенного третьего:

1.4.Закон введения отрицания:

1.5. Закон снятия двойного отрицания:

1.6. Законы идемпотентности:

Не останавливаясь на доказательствах простейших законов, приведём пример доказательства для закона 1.4.

Обозначим левую часть

Для неё получаем:

Этот результат утверждает справедливость данного закона.

2. Бинарные (двухслойные) законы. Они содержат два исходных высказывания и устанавливают основные соотношения этого уровня.

2.1. Законы коммутативности конъюнкции и дизъюнкции.

2.2. Закон контрапозиции:

2.3.Закон обратной контрапозиции:

2.4. Закон отрицания импликации:

2.5. Законы де Моргана:

2.6. Законы взаимосвязи бинарных операций:

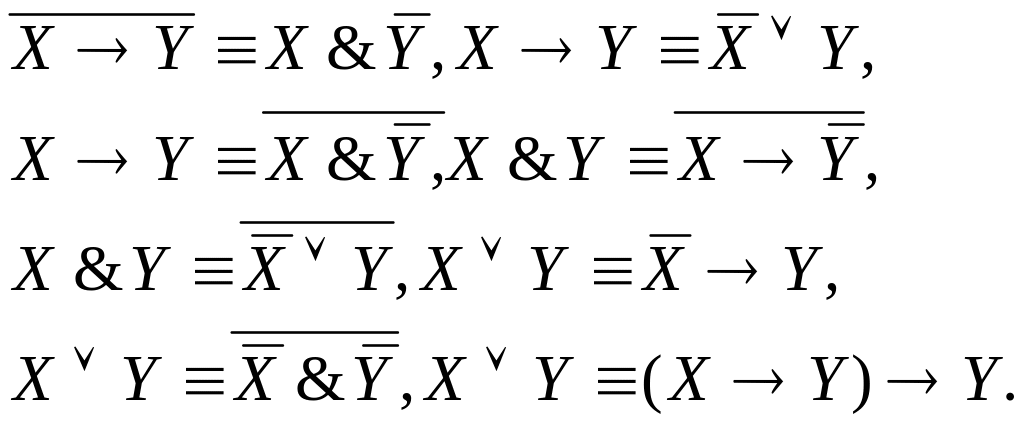
Доказательство этих формул предоставляем читателям.

3. Тернарные (трехслойные) законы.

Они содержат три исходных высказывания и устанавливают основные закономерности этого уровня. В реальности таких законов очень большое количество, поэтому мы рассмотрим только основные из них.

3.1. Законы ассоциативности конъюнкции и дизъюнкции:

3.2. Законы дистрибутивности конъюнкции и дизъюнкции:

3.3.Законы импликации:

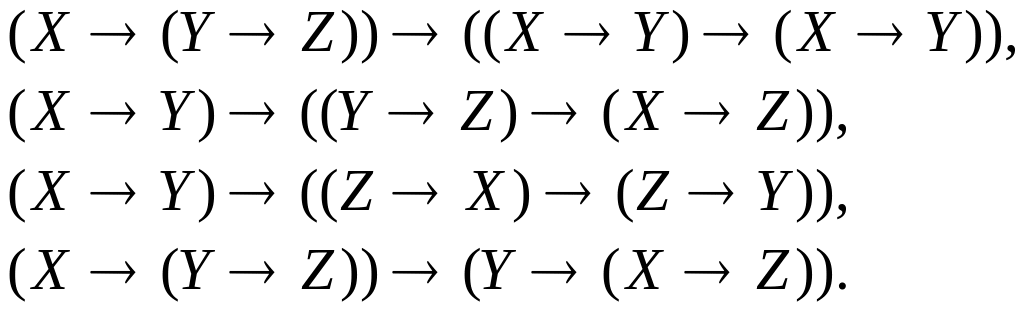
3.4. Законы переноса:

а) закон импортации

б) закон экспортации

3.5. Законы монотонности:

3.6. Законы сложной контрапозиции:

3.7. Законы силлогизма:

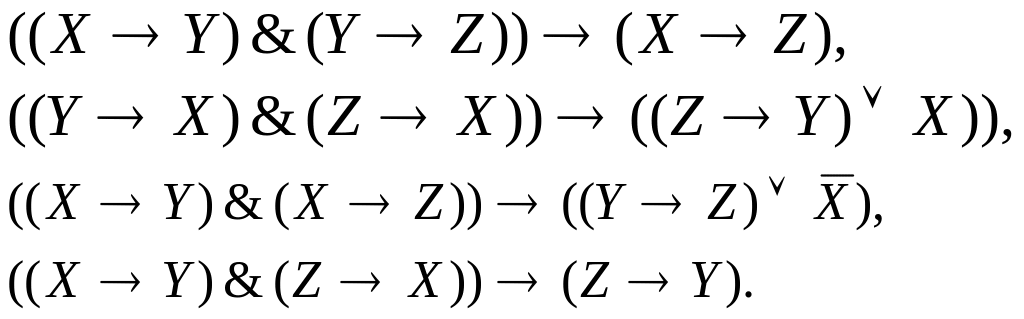
Выражения для второй, третьей и четвёртой фигур силлогизма указываются в исправленной форме.

3.8. Законы выявления:

4. Рассмотрим примеры доказательства некоторых из приведённых законов, предоставляя возможность читателю по предлагаемым схемам провести исследование других законов.

Докажем справедливость второго из законов сложной контрапозиции:

Для доказательства найдем функции истинности левой и правой частей и покажем их совпадение.

Введем обозначения:

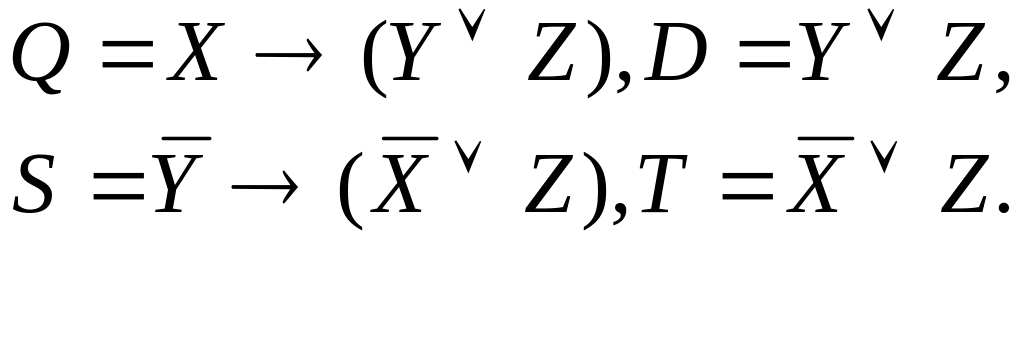
Теперь последовательно получаем для левой части:

Аналогично для формулы в правой части получаем последовательно,

учитывая введенные обозначения:

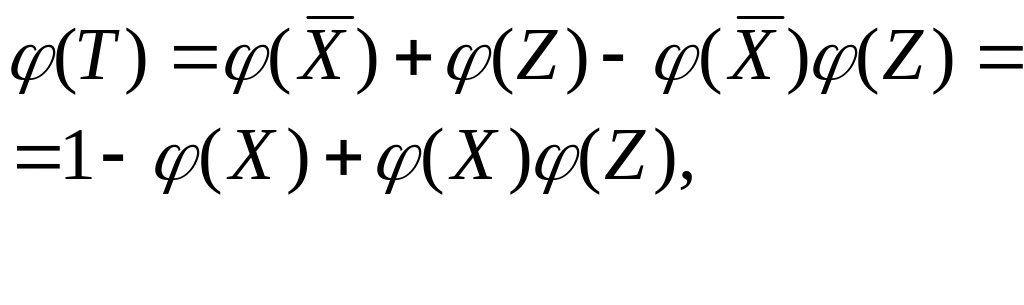
Таким образом, значения функций истинности в левой и правой частях совпадают, что означает справедливость рассматриваемой формулы.

5. Дадим теперь доказательство последней из приведённых формул силлогизма:

Заметим, что в данном случае нужно доказать справедливость всей формулы (как тавтологию). Для упрощения вычислений вводим обозначения:

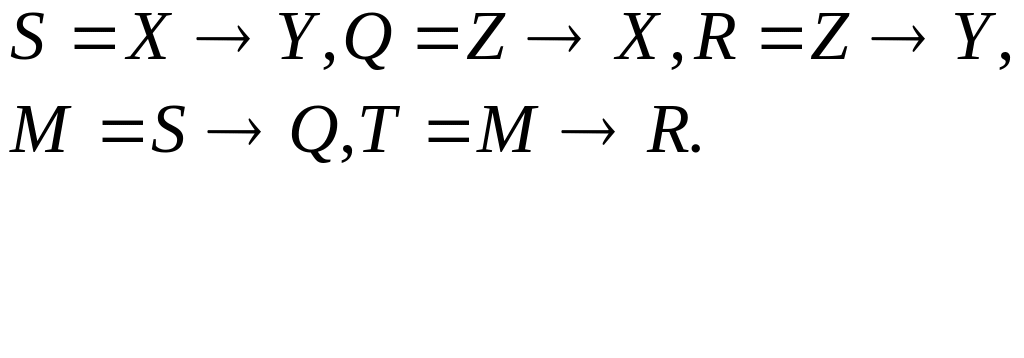
Малыми латинскими буквами будем обозначать значения функции истинности соответствующих высказываний. Так, получаем:

Последовательно вычисляем значения m и t, учитывая идемпотентность функции истинности:

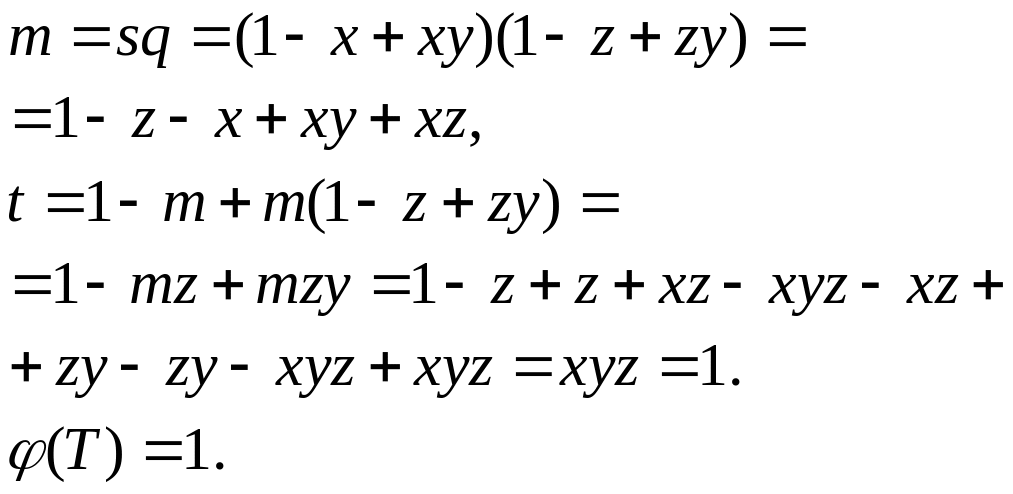
Это означает, что данная формула является законом логики.

Заметим, что только первая фигура силлогизма (см.. § 16), совпадает с приведёнными законами, а вторая, третья и четвёртая фигуры изменены для исключения дефектных блоков, присутствовавших в исходном виде.

Законы логики можно формулировать и как правила вывода, тогда их доказательство можно проводить в табличной форме. Рассмотрим в качестве примера доказательство второй формулы силлогизма (в виде преобразованном к закону логики), которую запишем как правило вывода:

Построим отдельно таблицы истинности тернарных операций,

указанных в числителе и знаменателе.

Числитель запишем в виде формулы:

Для него строим первичные матрицы:

X Y		X
	1	1
Y	0	1

X Z		X
	1	1
Z	0	1

По этим таблицам записываем рабочие блоки:

Эти выражения подставляем в формулу для Q и, с учётом идемпотентности бинарных операций, получаем:

Таким образом, эта формула содержит пять рабочих блоков.

Теперь записываем матрицу построенной тернарной операции, как это делалось в § 7.

Во всех случаях сравнения формул будем считать порядок аргументов традиционным (лексикографическим): {X,Y,Z}.

Приведём матрицу для формулы Q в числителе.

Z	Y X	0	1
0	0	1	0
0	1	1	1
1	0	0	0
1	1	1	1

Аналогично проводим анализ тернарной операции в знаменателе.

Здесь внутренняя бинарная операция имеет вид:

Поэтому получаем выражения для рабочих блоков:

Теперь находим всё выражение для знаменателя:

Для выражения Р также строим таблицу истинности в форме Карно.

Z	Y X	0	1
0	0	1	1
0	1	1	1
1	0	0	1
1	1	1	1

Сравнение таблиц истинности для Q и для Р приводит к выводу о выполнении и условий импликации:

Аналогично могут быть доказаны и другие логические законы.

Контрольные вопросы:

1. Общее представление о логических законах.

2. Логические законы первого уровня.

3. Примеры доказательства логических законов первого уровня.

4. Логические законы второго уровня.

5. Примеры доказательства логических законов второго уровня.

6. Логические законы третьего уровня.

7. Примеры доказательства логических законов третьего уровня.

8. Применение правил вывода к доказательству логических законов.