§ 15. Квадратичные логические операции.

Квадратичные логические операции (сокращенно «квадра-операции») могут быть нескольких типов: дважды бинарные и цепочные последовательности (четырех типов). Кратко рассмотрим их строение и методы вычисления.

Отметим, что мы всюду применяем матричные виды таблиц истинности, которые удачно раскрывают структуру этих операций. В общем случае матрица значений функции истинности для квадра – операции имеет вид

T		0	0	1	1
Z	Y X	0	1	0	1
0	0
0	1
1	0
1	1

Для каждого типичного случая таких операций матричная форма таблицы истинности конкретизируется с учётом реального вида формулы. Значения параметров операции принадлежат множеству {0;1}. Существует множество типов квадра – операций. Рассмотрим основные из них.

Дважды бинарные логические операции.

Они содержат две внутренние бинарные операции, связанные одной внешней логической операцией, поэтому выражаются формулой:

(15.1)

Каждую часть следует сначала рассмотреть отдельно как бинарную операцию, затем, также отдельно, построить внешнюю бинарную операцию, и лишь после этого соединить все результаты в одну формулу. Рассмотрим сначала первую внутреннюю бинарную операцию:

(15.2).

Для неё получаем таблицу истинности:

Y X	0	1
0
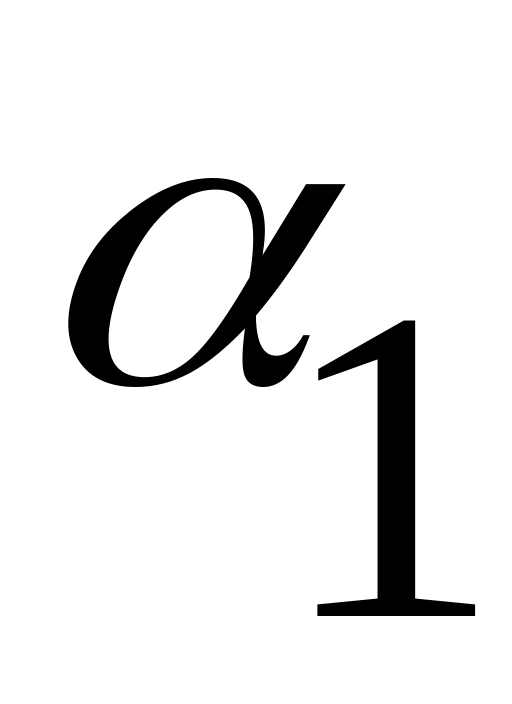
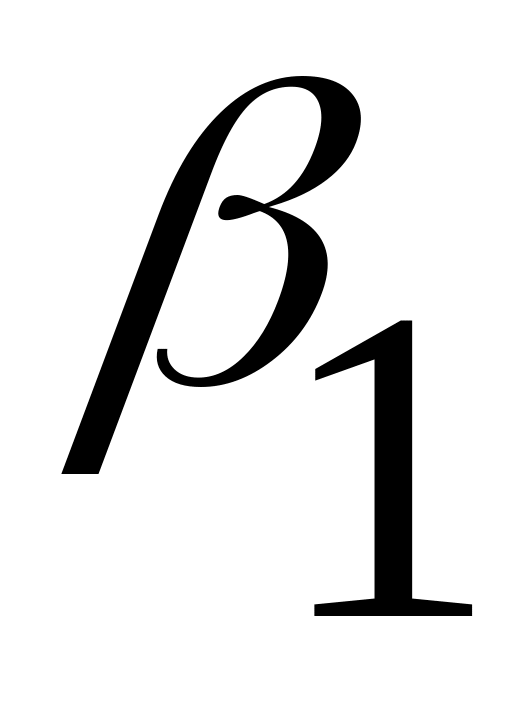
1

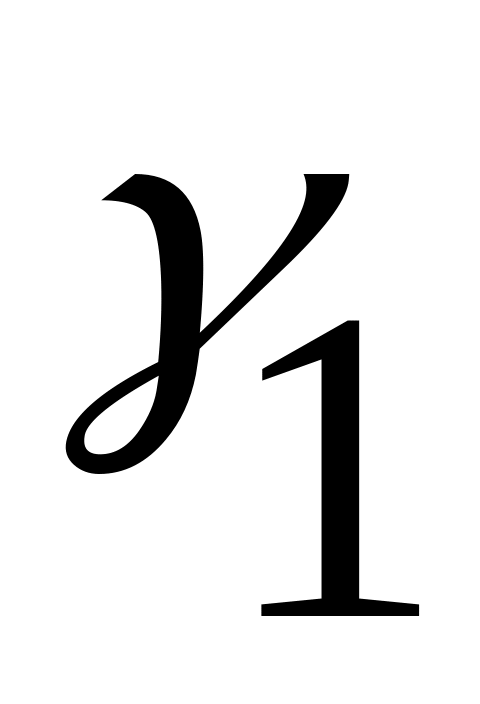
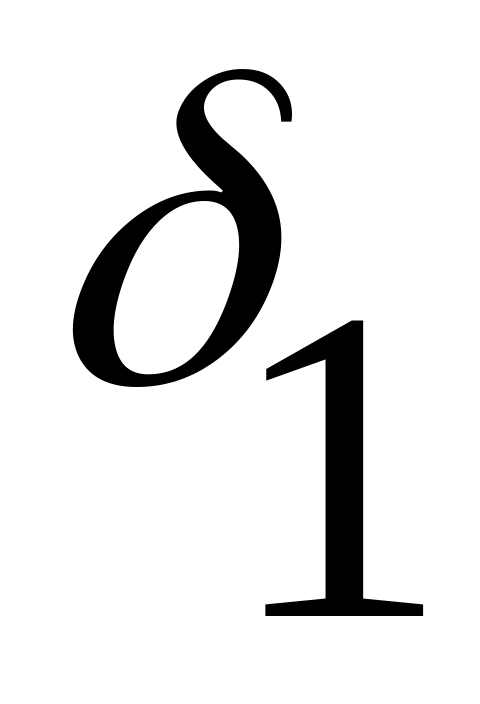
и формулу рабочих блоков:

(15.3)

Для взаимной к ней операции получим:

(15.4)

Аналогично строится и вторая внутренняя бинарная операция:

Для неё мы тоже запишем таблицу истинности

T Z	0	1
0
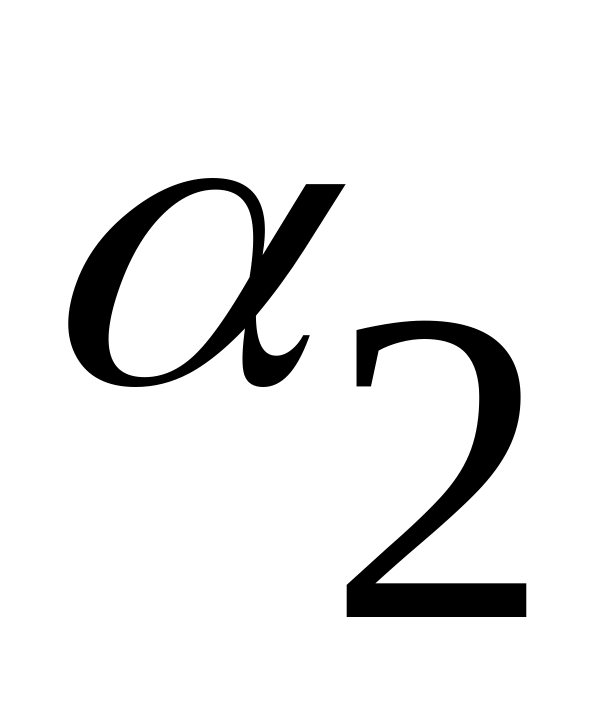
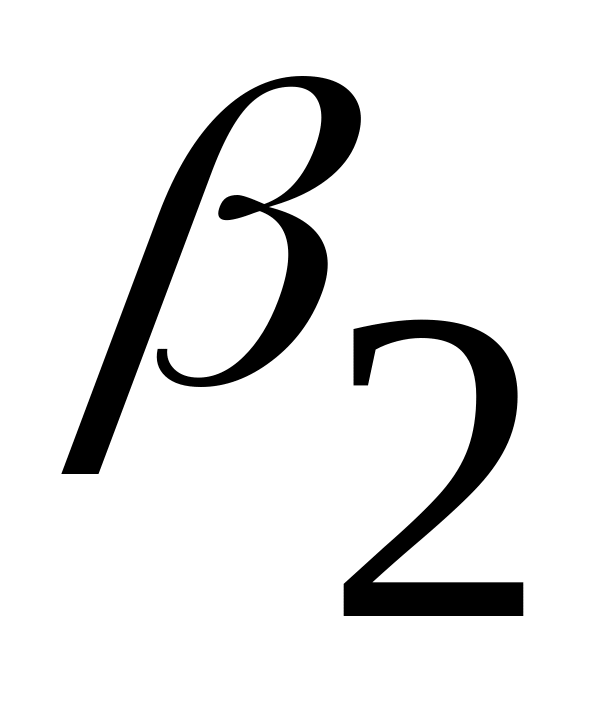
1

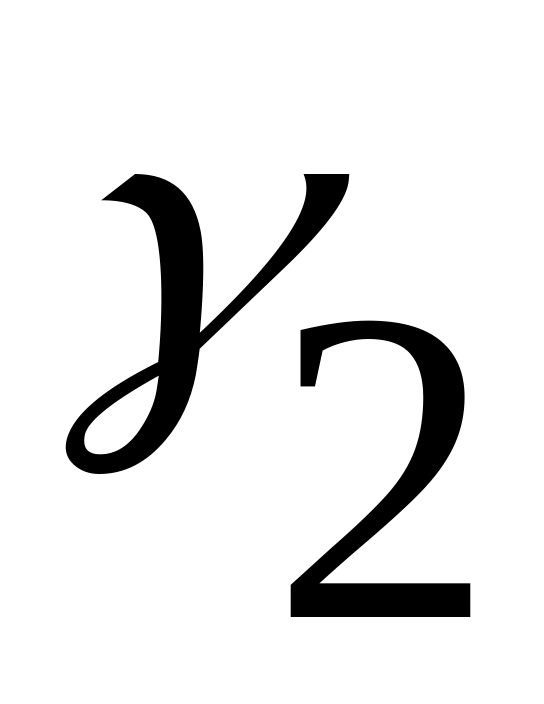
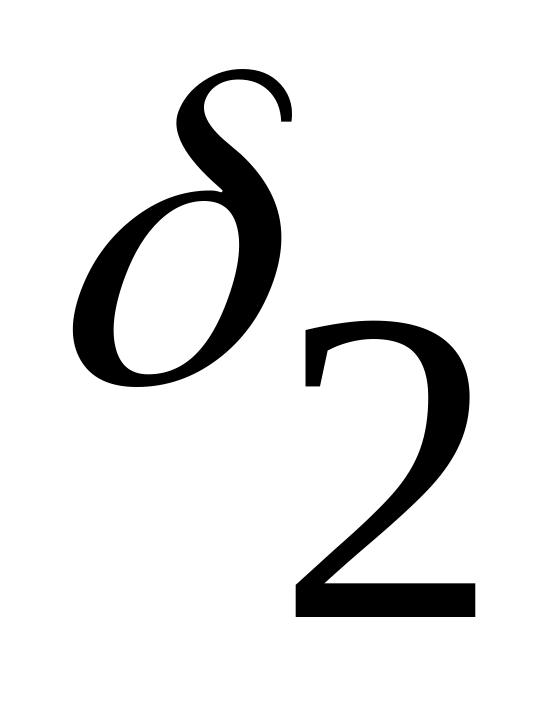
и формулу рабочих блоков:

. (15.5)

Для взаимной к ней операции получаем формулу:

. (15.6)

Теперь строим внешнюю бинарную операцию:

Для этой операции также строим свою таблицу истинности

N M	0	1
0
1

и формулу рабочих блоков:

(15.7).

Обозначим выражения логических блоков квадра – операции в виде матрицы Тогда для этой матрицы получаем таблицу:

j i	1	2	3	4
1
2
3
4

Таким образом, символьный массив квадра – операции можно представить

в виде

T Q		0	0	1	1
Z	Y X	0	1	0	1
0	0
0	1
1	0
1	1

Значения выражений определяются как произведения соответствующих высказываний или их отрицаний:

= , = , = , = ,

= , = , = , = , (15.8)

= , = , = , = ,

= , = , = , = .

Кроме этого вида для квадра – операций применяется структура «поля Канта»

Q
		0000			0100	0001	0101
		1000			1100	1001	1101

Учитывая выражения для матриц истинности внутренних операций, получим значения матрицы истинности внешней бинарной операции, которую будем структурировать аналогично с приведённым выше символьным массивом. При этом следует учитывать, что при внешнем отрицании во внутренних операциях изменяется сам вид матриц истинности. Таким образом, теперь мы находим явный вид матрицы истинности квадра – операции, как алгебраической структуры, соответствующей полю Канта (для рабочих блоков значения матрицы истинности равны 1, а для нерабочих они равны 0).

Примечание: в конкретных задачах изображение поля Канта упрощается, так как четырёхзначные шифры блоков не пишутся.

Матрица определяется через значения матриц истинности двух внутренних и одной внешней бинарных операций:

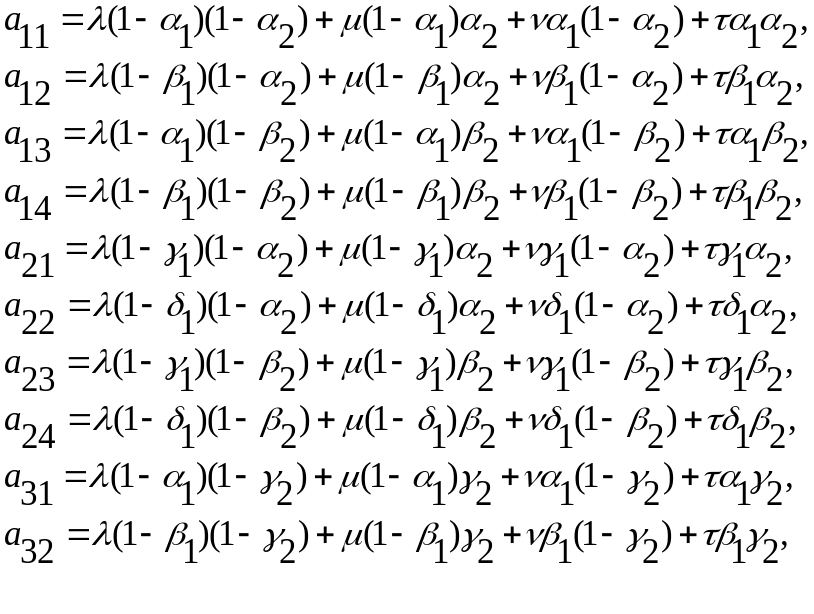(15.9)

«Цепочные» квадратичные операции.

Существует четыре различных по смыслу случая «цепочных» квадратичных операций:

а) каждое последующее высказывание, кроме первых двух, объединённых внутренней бинарной операцией, является внешним по отношению к предыдущей формуле:

(15.10)

б) два внутренних высказывания объединены в одну операцию, а последнее высказывание является внешним:

(15.11)

в) первое высказывание является внешним, а второе и третье объединены в одну операцию:

(15.12)

г) Первое высказывание является внешним, а внутренняя бинарная операция объединяет два последних высказывания:

(15.13)

Рассмотрим подробно первую из этих формул, а остальные схемы аналогичны.

Итак, пусть известна «цепочная» квадра – операция первого вида.

Для неё получаем последовательность «вложенных» бинарных операций:

Каждую из этих операций анализируем как бинарную.

Мы не будем записывать стандартные виды структуры четырех блоков каждой операции, а сразу укажем виды рабочих блоков заданной и взаимной бинарных операций.

Для первой бинарной операции в этой цепочке получаем:

(15.14)

Аналогично находим для второй операции этой цепочки:

(15.15)

Третья операция этой цепочки является финальной и рассматривается условно как внешняя. Для неё получаем исходное выражение:

(15.16)

Промежуточную операцию (N) проанализируем как тернарную операцию первого типа:

(15.17)

Для неё получаем таблицу матрицы истинности:

Z	Y X	0	1
0 0	0
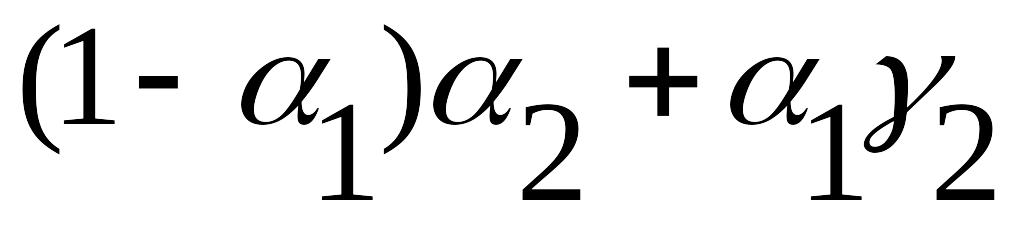
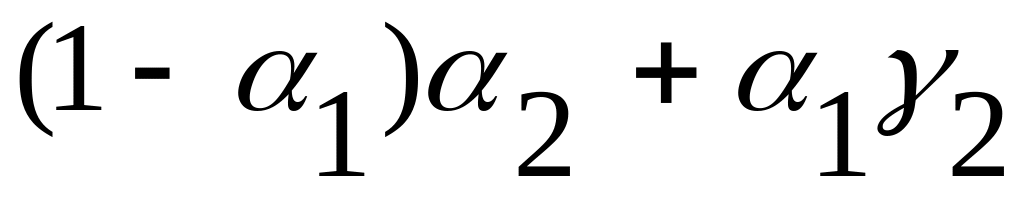
	1
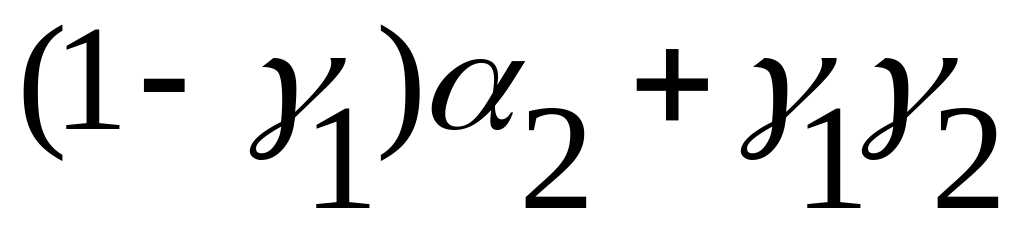
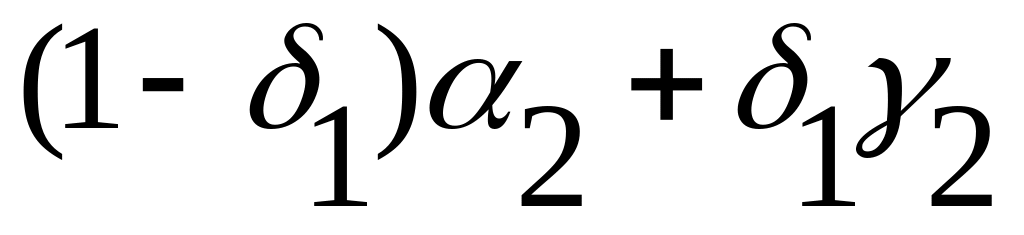
1	0
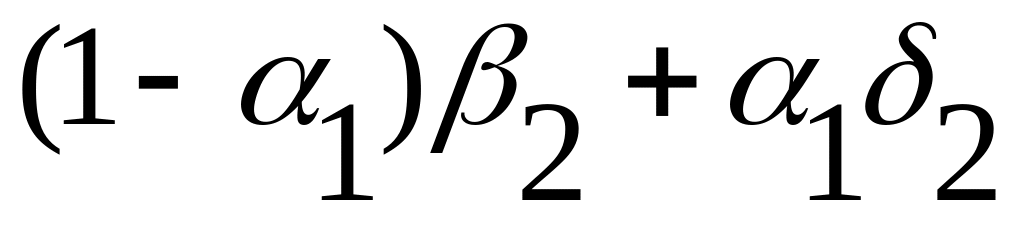
	1

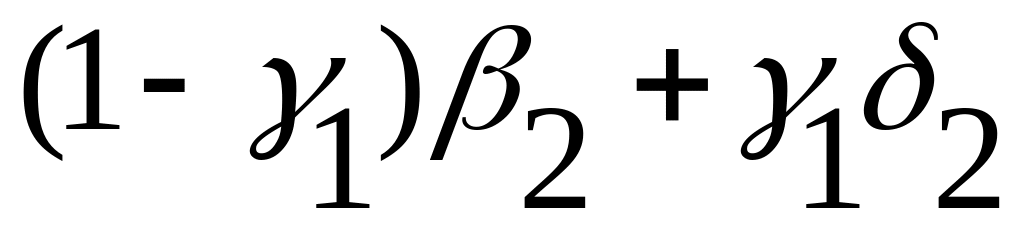
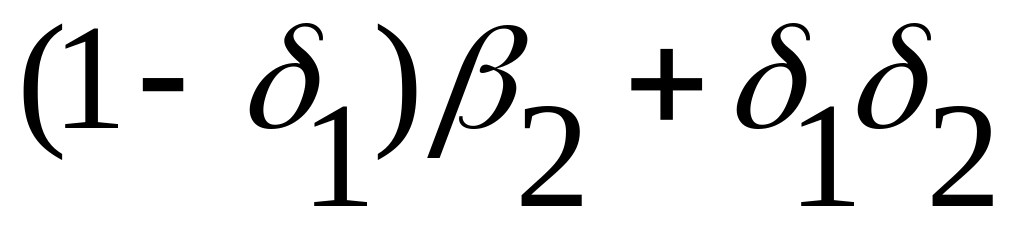
Аналогично строится таблица истинности для отрицания промежуточной операции ( ), из которой затем конструируется выражение для всей операции Q. Мы приведём только вид матрицы для отрицания промежуточной операции, а окончательную формулу можно записать в виде значений матрицы истинности всей цепочной квадратичной операции. Взаимная к формуле (14.17) операция имеет матрицу истинности:

Z	Y X	0	1
0 0	0
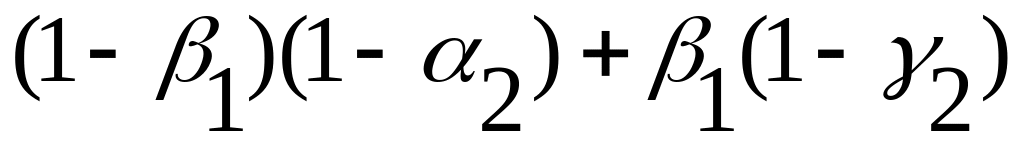
	1
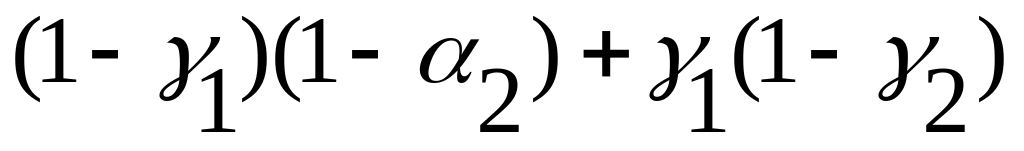
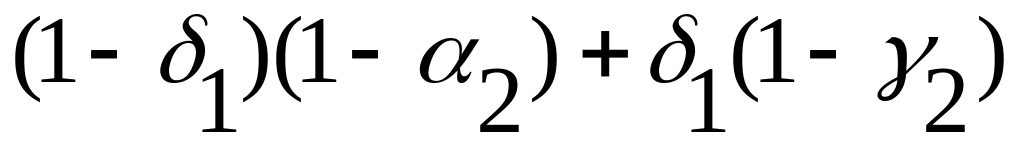
1	0
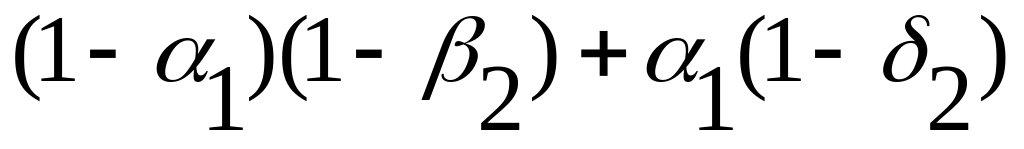
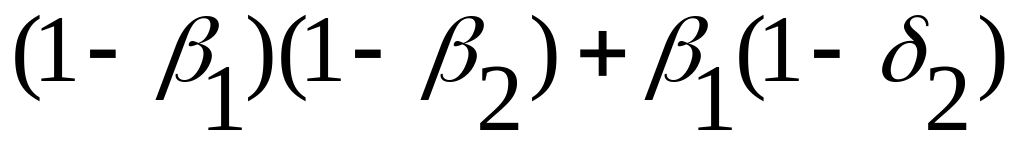
	1

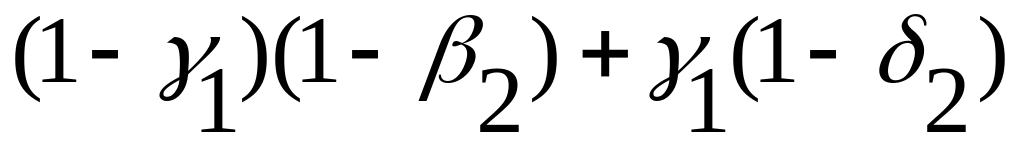
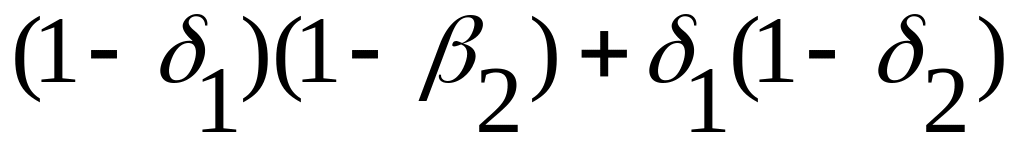
Полную запись всех значений матрицы истинности в этом случае мы оставим читателям для самостоятельной работы.

Аналогично могут быть проанализированы и другие виды «цепочных» квадратичных операций.

Контрольные вопросы:

1. Понятие о квадратичных логических операциях.

2. Дважды бинарная логическая операция.

3. Символьный массив дважды бинарной квадра – операции.

4. Поле Канта дважды бинарной квадра – операции.

5. Матрица истинности дважды бинарной квадра – операции.

6. Виды «цепочных» квадра – операций.

7. Анализ «цепочной» квадра-операции первого вида.

8. Применение квадра – операций. Примеры.